ГДЗ по Алгебре 10-11 Класс Номер 720 Алимов — Подробные Ответы

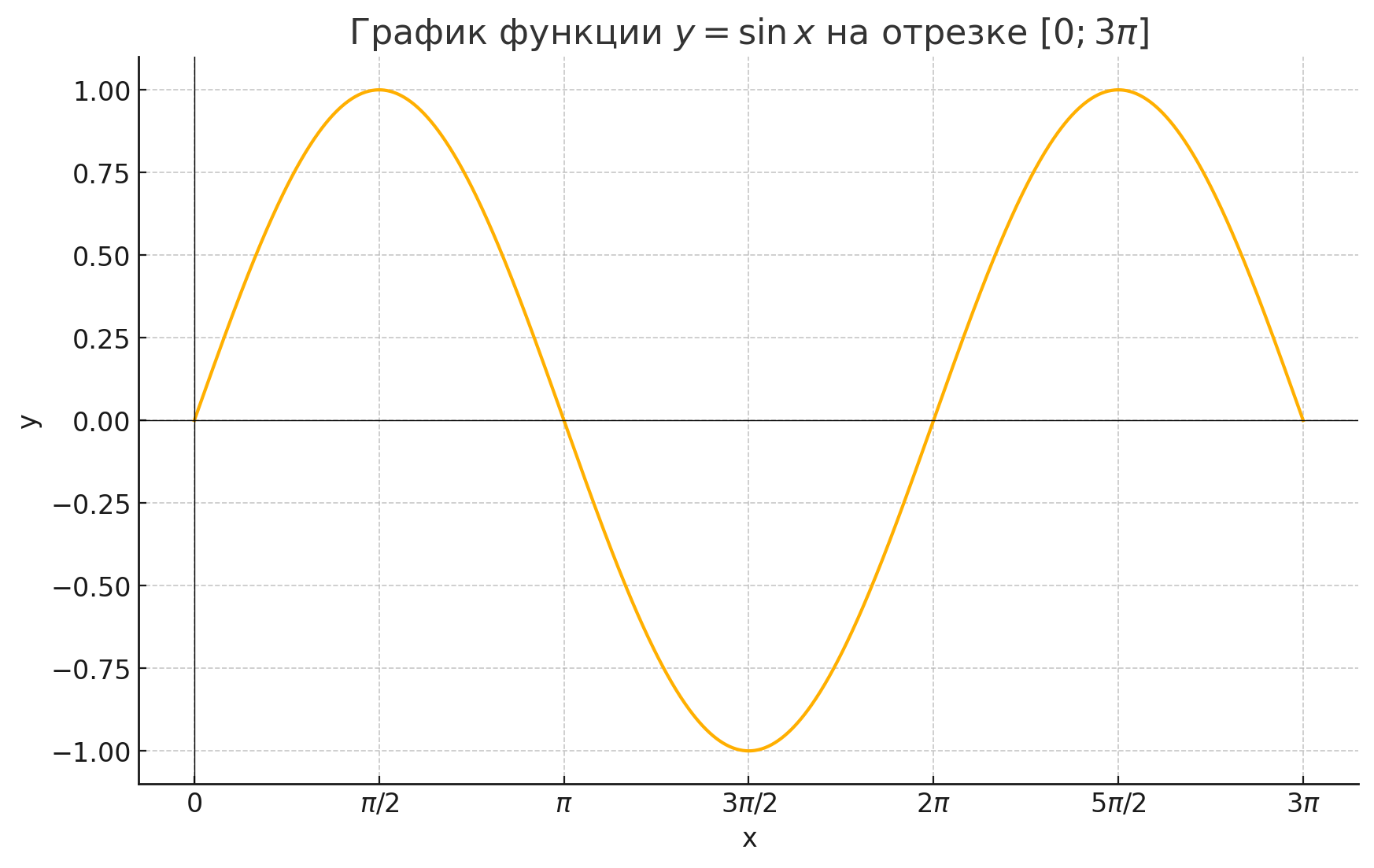
Пользуясь графиком функции у = sin х, выполнить упражнения (720—725).

(Устно.) Выяснить, при каких значениях х, принадлежащих отрезку [0; 3пи], функция у = sin х принимает:

1. значение, равное 0, 1, -1;
2. положительные значения;
3. отрицательные значения.

Воспользуемся графиком функции $y=\sin x$ на отрезке $[0;3\pi ]$:

1. Функция принимает значение, равное:
   $y=0$ при $x=0,\pi ,2\pi ,3\pi$;
   $y=1$ при $x=\frac{\pi }{2},\frac{5\pi }{2}$;
   $y=-1$ при $x=\frac{3\pi }{2}$;
2. Функция принимает положительные значения при:
   $0<x<\pi$ и $2\pi <x<3\pi$;
3. Функция принимает отрицательные значения при:
   $\pi <x<2\pi$

Используя график функции $y=\sin x$ на отрезке $[0;3\pi ]$, нужно:

1. Найти значения функции в ключевых точках;
2. Определить промежутки, где функция принимает положительные значения;
3. Определить промежутки, где функция принимает отрицательные значения.

Шаг 1. Анализ функции и её графика

Функция $y=\sin x$ — это классическая тригонометрическая функция с периодом $2\pi$. Это значит, что её график повторяется каждые $2\pi$ по оси $x$.

• На интервале $[0,3\pi ]$ у нас покрывается полтора периода функции, так как $3\pi =1.5\times 2\pi$.
• Функция синуса начинается в нуле при $x=0$, поднимается до максимума 1, опускается до минимума -1 и возвращается к нулю через полный период.

Шаг 2. Точки, где функция равна нулю

Нули функции $y=\sin x$ — это точки, в которых синус равен нулю. Знаем из тригонометрии, что синус равен нулю в точках:

$$x=k\pi ,k\in \mathbb{Z}$$

На отрезке $[0;3\pi ]$ это:

$$x=0,\pi ,2\pi ,3\pi$$

В этих точках:

$$y=\sin x=0$$

Шаг 3. Точки максимума и минимума

Максимум функции $y=\sin x$ равен 1, достигается в точках:

$$x=\frac{\pi }{2}+2k\pi ,k\in \mathbb{Z}$$

Минимум функции равен -1, достигается в точках:

$$x=\frac{3\pi }{2}+2k\pi ,k\in \mathbb{Z}$$

На интервале $[0;3\pi ]$:

• Максимум $y=1$ достигается при $x=\frac{\pi }{2}$ и при $x=\frac{5\pi }{2}$ поскольку $\frac{5\pi }{2}=\frac{\pi }{2}+2\pi$;
• Минимум $y=-1$ достигается при $x=\frac{3\pi }{2}$.

Шаг 4. Промежутки знакопостоянства функции

Синус — функция, которая меняет знак при каждом нуле. Посмотрим, где она положительна и где отрицательна.

• На промежутке $(0,\pi )$:
  Значения синуса положительны, так как график синуса от 0 поднимается до 1 (в $\frac{\pi }{2}$), а затем опускается обратно до 0 (в $\pi$).
• На промежутке $(\pi ,2\pi )$:
  Синус принимает отрицательные значения, т.к. функция убывает от 0 в $\pi$ до -1 в $\frac{3\pi }{2}$, а затем поднимается обратно к 0 в $2\pi$.
• На промежутке $(2\pi ,3\pi )$:
  Функция снова принимает положительные значения, поднимаясь с 0 до 1 в $\frac{5\pi }{2}$, затем снова убывает к 0 в $3\pi$.

Итоговые ответы

• Значения функции в ключевых точках:

$$\{\begin{array}{ll}y=0& \text{при }x=0,\pi ,2\pi ,3\pi ;\\ y=1& \text{при }x=\frac{\pi }{2},\frac{5\pi }{2};\\ y=-1& \text{при }x=\frac{3\pi }{2}\mathrm{.}\end{array}$$

• Положительные значения функции:

$$0<x<\pi \text{и}2\pi <x<3\pi$$

• Отрицательные значения функции:

$$\pi <x<2\pi$$

Дополнительная иллюстрация

• Точки $x=0,\pi ,2\pi ,3\pi$ — пересечения графика с осью $x$.
• Точки максимумов $x=\frac{\pi }{2},\frac{5\pi }{2}$ — пиковые точки графика на положительной высоте.
• Точка минимума $x=\frac{3\pi }{2}$ — пик внизу графика.