ГДЗ по Алгебре 10-11 Класс Номер 400 Алимов — Подробные Ответы

Построить график функции:

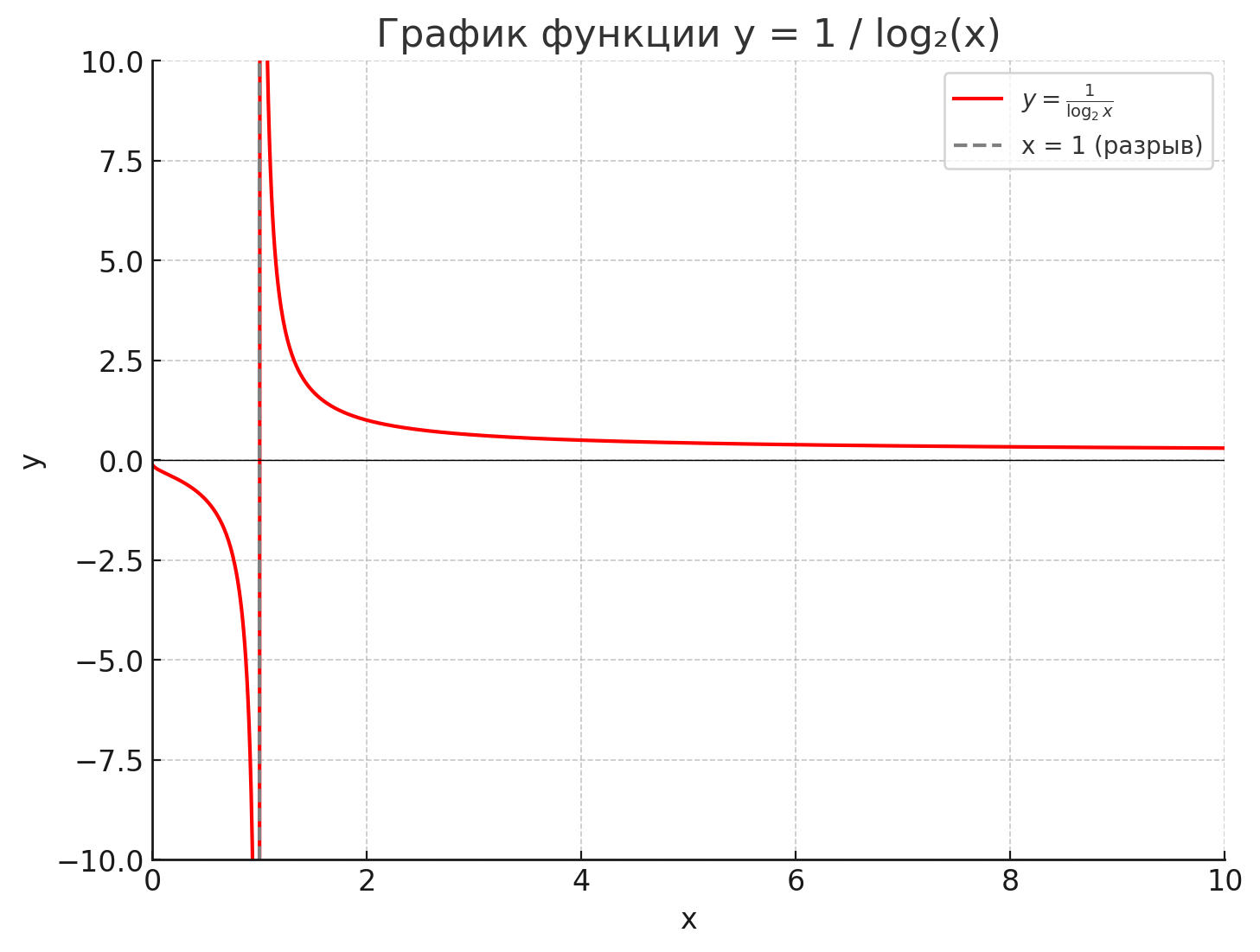
1. y=1/log2(x);
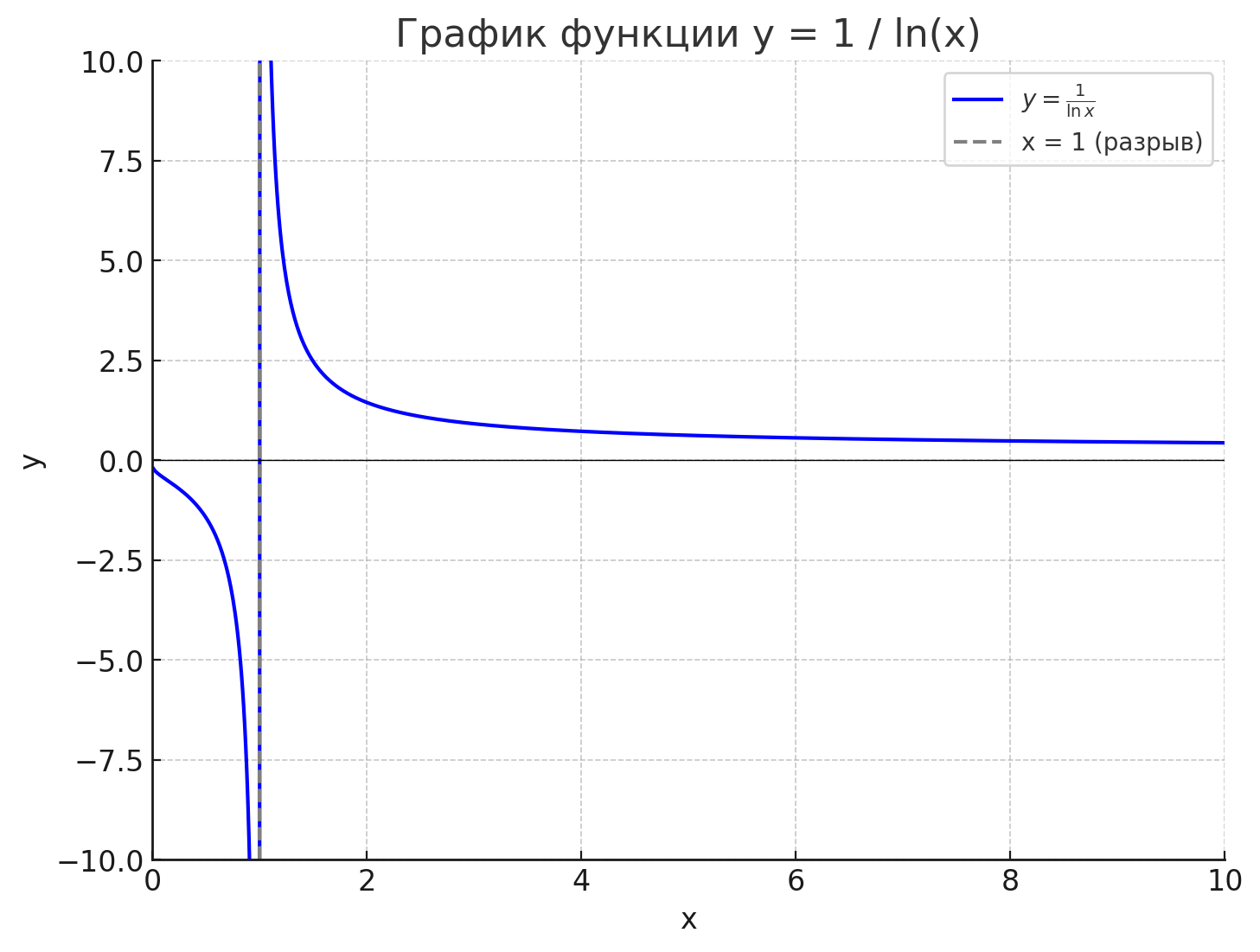
2. y=1/lnx.

1) $y=\frac{1}{{\log }_{2}x}$

• Область определения: $x>0$ и $x\mathrm{\ne }1$;
• Множество значений: $y\mathrm{\ne }0$;
• Функция убывает, так как: $2>1$;
• Координаты некоторых точек: $y(2)=1$;

График функции:

2) $y=\frac{1}{\ln x}$

• Область определения: $x>0$ и $x\mathrm{\ne }1$;
• Множество значений: $y\mathrm{\ne }0$;
• Функция убывает, так как: $e>1$;
• Координаты некоторых точек: $y(e)=1$;

График функции:

Функция 1: $y=\frac{1}{{\log }_{2}x}$

Шаг 1. Область определения

Функция содержит логарифм ${\log }_{2}x$. Вспомним основные свойства логарифма:

• ${\log }_{2}x$ определён только при $x>0$,
• выражение ${\log }_{2}x$ не должно быть равно нулю, так как деление на ноль не определено.

Когда ${\log }_{2}x=0$?
Решаем:

$${\log }_{2}x=0\Rightarrow x=2^0=1$$

Значит, при $x=1$ функция не определена.

Вывод:

$$\boxed{{\displaystyle \text{Область определения: }x>0,x\mathrm{\ne }1}}$$

Шаг 2. Множество значений

Функция принимает вид:

$$y=\frac{1}{{\log }_{2}x}$$

Поскольку ${\log }_{2}x\mathrm{\ne }0$, то:

• знаменатель не равен нулю,
• следовательно, $y\mathrm{\ne }0$.

Вывод:

$$\boxed{{\displaystyle \text{Множество значений: }y\mathrm{\ne }0}}$$

Шаг 3. Поведение функции (монотонность)

Исследуем, возрастает или убывает функция.

Функция убывает, если при увеличении $x$, значение $y$ уменьшается.

Так как:

• ${\log }_{2}x$ — возрастающая функция при $x>0$,
• а $y=\frac{1}{{\log }_{2}x}$ — обратная к ней,

то при увеличении $x$, логарифм возрастает, а его обратное значение убывает.

Вывод:

$$\boxed{{\displaystyle \text{Функция убывает, так как }2>1}}$$

Шаг 4. Значение в точке $x=2$

Подставим $x=2$ в формулу:

$$y(2)=\frac{1}{{\log }_{2}2}=\frac{1}{1}=1$$

Вывод:

$$\boxed{{\displaystyle y(2)=1}}$$

Шаг 5. Асимптоты и особые точки

• При $x\to 1^{-}$ и $x\to 1^{+}$: ${\log }_{2}x\to 0$, а $y\to \pm \mathrm{\infty }$.
  Значит, вертикальная асимптота при $x=1$.
• При $x\to 0^{+}$, ${\log }_{2}x\to -\mathrm{\infty }$, значит $y\to 0^{-}$.
  При $x\to +\mathrm{\infty }$, ${\log }_{2}x\to +\mathrm{\infty }$, значит $y\to 0^{+}$.
  Это значит: горизонтальная асимптота $y=0$, но сама точка $y=0$ не достигается.

Шаг 6. График функции

График проходит:

• справа от вертикальной асимптоты $x=1$, убывает от $+\mathrm{\infty }$ до 0,
• слева от неё — убывает от 0 до $-\mathrm{\infty }$.

Ключевая точка: $(2,1)$

Функция 2: $y=\frac{1}{\ln x}$

Шаг 1. Область определения

Аналогично:

• Логарифм $\ln x$ определён при $x>0$,
• $\ln x\mathrm{\ne }0\Rightarrow x\mathrm{\ne }1$ (так как $\ln 1=0$).

Вывод:

$$\boxed{{\displaystyle \text{Область определения: }x>0,x\mathrm{\ne }1}}$$

Шаг 2. Множество значений

Функция:

$$y=\frac{1}{\ln x}$$

• $\ln x\mathrm{\ne }0\Rightarrow y\mathrm{\ne }0$

Вывод:

$$\boxed{{\displaystyle \text{Множество значений: }y\mathrm{\ne }0}}$$

Шаг 3. Поведение функции (убывает)

• $\ln x$ — возрастает при $x>0$,
• $y=\frac{1}{\ln x}$ — убывает (обратная функция).

Вывод:

$$\boxed{{\displaystyle \text{Функция убывает, так как }e>1}}$$

Шаг 4. Значение в точке $x=e$

Вспомним: $\ln e=1$

$$y(e)=\frac{1}{\ln e}=\frac{1}{1}=1$$

Вывод:

$$\boxed{{\displaystyle y(e)=1}}$$

Шаг 5. Асимптоты и поведение

• При $x\to 1^{\pm }$, $\ln x\to 0$, значит $y\to \pm \mathrm{\infty }$ — вертикальная асимптота при $x=1$
• При $x\to 0^{+}$: $\ln x\to -\mathrm{\infty }\Rightarrow y\to 0^{-}$
• При $x\to +\mathrm{\infty }$: $\ln x\to +\mathrm{\infty }\Rightarrow y\to 0^{+}$

Горизонтальная асимптота: $y=0$

Шаг 6. График функции

• Слева и справа от точки $x=1$ — разрыв второго рода
• Функция убывает
• График проходит через точку $(e,1)\approx (2.718,1)$