ГДЗ по Алгебре 10-11 Класс Номер 332 Алимов — Подробные Ответы

Построить график функции, найти её область определения и множество значений:

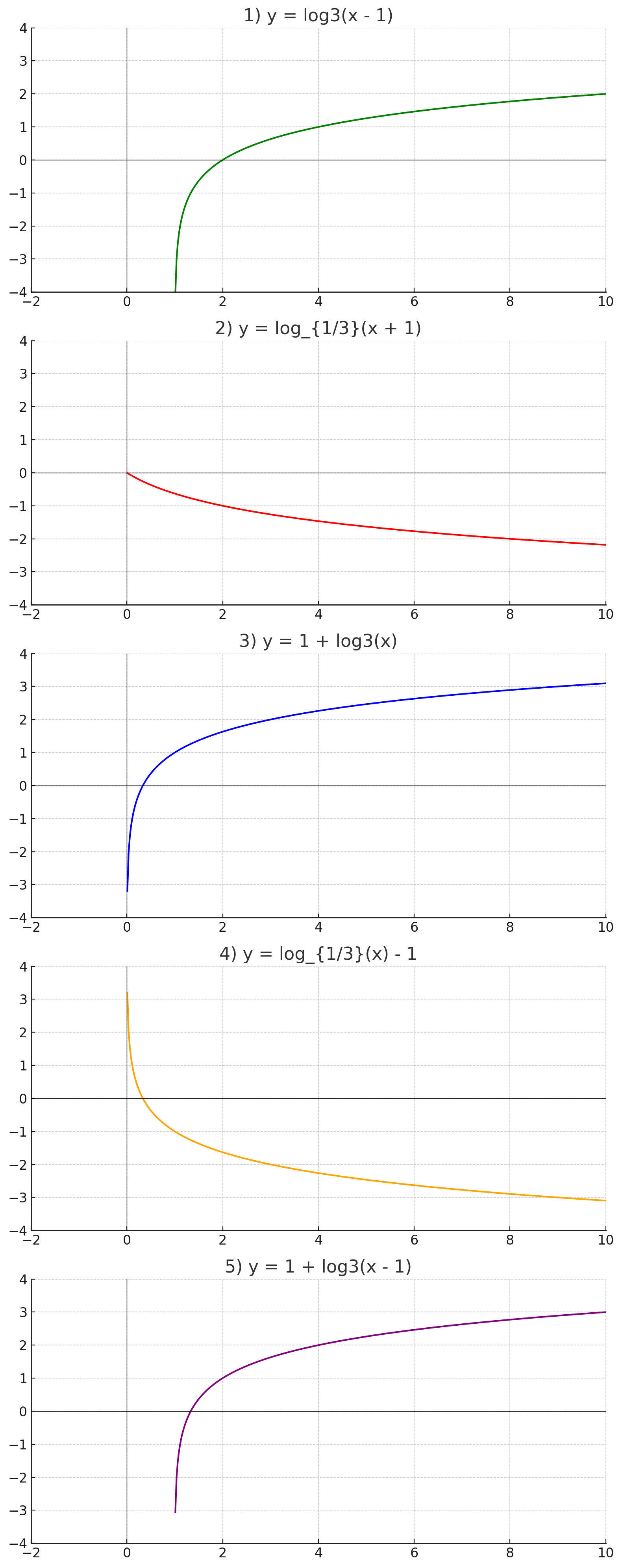
1. y= log3(x-1);
2. y= log1/3(x+1);
3. y= 1+log3(x);
4. y= log1/3(x-1);
5. y= 1+ log3(x-1).

1) $y={\log }_3(x-1)$

Рассмотрим функцию $y={\log }_{3}x$:

• Область определения: $x>0$;
• Множество значений: $y\in \mathbb{R}$;
• Функция возрастает, так как $3>1$;

Таблица значений:

$$\begin{array}{cccc}x& 1& 3& 9\\ y& 0& 1& 2\end{array}$$

Построим график функции $y={\log }_{3}x$ и осуществим его сдвиг вдоль оси абсцисс на 1 единицу вправо

Ответ:

$$D(x)=(1;+\mathrm{\infty });E(y)=(-\mathrm{\infty };+\mathrm{\infty })\mathrm{.}$$

2) $y={\log }_{\frac{1}{3}}(x+1)$

Рассмотрим функцию $y={\log }_{\frac{1}{3}}x$:

• Область определения: $x>0$;
• Множество значений: $y\in \mathbb{R}$;
• Функция убывает, так как $0<\frac{1}{3}<1$;

Таблица значений:

$$\begin{array}{cccc}x& 1& 3& 9\\ y& 0& -1& -2\end{array}$$

Построим график функции $y={\log }_{\frac{1}{3}}x$ и осуществим его сдвиг вдоль оси абсцисс на 1 единицу влево

Ответ:

$$D(x)=(-1;+\mathrm{\infty });E(y)=(-\mathrm{\infty };+\mathrm{\infty })\mathrm{.}$$

3) $y=1+{\log }_{3}x$

Рассмотрим функцию $y={\log }_{3}x$:

• Область определения: $x>0$;
• Множество значений: $y\in \mathbb{R}$;
• Функция возрастает, так как $3>1$;

Таблица значений:

$$\begin{array}{cccc}x& 1& 3& 9\\ y& 0& 1& 2\end{array}$$

Построим график функции $y={\log }_{3}x$ и осуществим его сдвиг вдоль оси ординат на 1 единицу вверх

Ответ:

$$D(x)=(0;+\mathrm{\infty });E(y)=(-\mathrm{\infty };+\mathrm{\infty })\mathrm{.}$$

4) $y={\log }_{\frac{1}{3}}x-1$

Рассмотрим функцию $y={\log }_{\frac{1}{3}}x$:

• Область определения: $x>0$;
• Множество значений: $y\in \mathbb{R}$;
• Функция убывает, так как $0<\frac{1}{3}<1$;

Таблица значений:

$$\begin{array}{cccc}x& 1& 3& 9\\ y& 0& -1& -2\end{array}$$

Построим график функции $y={\log }_{\frac{1}{3}}x$ и осуществим его сдвиг вдоль оси ординат на 1 единицу вниз

Ответ:

$$D(x)=(0;+\mathrm{\infty });E(y)=(-\mathrm{\infty };+\mathrm{\infty })\mathrm{.}$$

5) $y=1+{\log }_3(x-1)$

Рассмотрим функцию $y={\log }_{3}x$:

• Область определения: $x>0$;
• Множество значений: $y\in \mathbb{R}$;
• Функция возрастает, так как $3>1$;

Таблица значений:

$$\begin{array}{cccc}x& 1& 3& 9\\ y& 0& 1& 2\end{array}$$

Построим график функции $y={\log }_{3}x$ и осуществим его сдвиг вдоль оси абсцисс на 1 единицу вправо и вдоль оси ординат на 1 единицу вверх

Ответ:

$$D(x)=(1;+\mathrm{\infty });E(y)=(-\mathrm{\infty };+\mathrm{\infty })\mathrm{.}$$

1) $y={\log }_3(x-1)$

Шаг 1: Базовая функция

Возьмём стандартную логарифмическую функцию:

$$y={\log }_{3}x$$

• Основание $3>1$, значит функция возрастает.
• Область определения: $x>0$
• Множество значений: $y\in \mathbb{R}$

Шаг 2: Таблица значений

Для функции $y={\log }_{3}x$:

$$\begin{array}{cccc}x& 1& 3& 9\\ y& 0& 1& 2\end{array}$$

Шаг 3: Сдвиг по оси x

Функция $y={\log }_3(x-1)$ — это горизонтальный сдвиг $y={\log }_{3}x$ вправо на 1 единицу.
Все x-координаты увеличиваются на 1:

$$\begin{array}{cccc}x& 2& 4& 10\\ y& 0& 1& 2\end{array}$$

Шаг 4: Область определения

$$x-1>0\Rightarrow x>1$$

Обозначим:

$$D(x)=(1;+\mathrm{\infty })$$

Шаг 5: Множество значений

Логарифмическая функция определена на всей числовой прямой:

$$E(y)=(-\mathrm{\infty };+\mathrm{\infty })$$

2) $y={\log }_{\frac{1}{3}}(x+1)$

Шаг 1: Базовая функция

Возьмём $y={\log }_{\frac{1}{3}}x$:

• Основание $\frac{1}{3}<1$, $>0$: функция убывает
• Область определения: $x>0$
• Значения: $y\in \mathbb{R}$

Шаг 2: Таблица значений

$$\begin{array}{cccc}x& 1& 3& 9\\ y& 0& -1& -2\end{array}$$

Шаг 3: Сдвиг влево на 1

Преобразование: $y={\log }_{\frac{1}{3}}(x+1)$
Значит, все x уменьшаются на 1:

$$\begin{array}{cccc}x& 0& 2& 8\\ y& 0& -1& -2\end{array}$$

Шаг 4: Область определения

$$x+1>0\Rightarrow x>-1$$$$D(x)=(-1;+\mathrm{\infty })$$

Шаг 5: Значения

$$E(y)=(-\mathrm{\infty };+\mathrm{\infty })$$

3) $y=1+{\log }_{3}x$

Шаг 1: Базовая функция

Опять берём $y={\log }_{3}x$

Шаг 2: Таблица значений

$$\begin{array}{cccc}x& 1& 3& 9\\ y& 0& 1& 2\end{array}$$

Шаг 3: Сдвиг вверх

$y={\log }_{3}x+1$: вертикальный сдвиг на 1 единицу вверх:
Все y увеличиваются на 1:

$$\begin{array}{cccc}x& 1& 3& 9\\ y& 1& 2& 3\end{array}$$

Шаг 4: Область определения

$$x>0\Rightarrow D(x)=(0;+\mathrm{\infty })$$

Шаг 5: Значения

$$E(y)=(-\mathrm{\infty };+\mathrm{\infty })$$

4) $y={\log }_{\frac{1}{3}}x-1$

Шаг 1: Исходная функция

Базовая: $y={\log }_{\frac{1}{3}}x$, убывает

Шаг 2: Таблица значений

$$\begin{array}{cccc}x& 1& 3& 9\\ y& 0& -1& -2\end{array}$$

Шаг 3: Сдвиг вниз на 1

$y={\log }_{\frac{1}{3}}x-1$ — уменьшаем каждое значение y на 1:

$$\begin{array}{cccc}x& 1& 3& 9\\ y& -1& -2& -3\end{array}$$

Шаг 4: Область определения

$$x>0\Rightarrow D(x)=(0;+\mathrm{\infty })$$

Шаг 5: Значения

$$E(y)=(-\mathrm{\infty };+\mathrm{\infty })$$

5) $y=1+{\log }_3(x-1)$

Шаг 1: Исходная функция

Возьмём $y={\log }_{3}x$, затем применим два преобразования:

• Горизонтальный сдвиг вправо на 1
• Вертикальный сдвиг вверх на 1

Шаг 2: Таблица значений

Для $y={\log }_{3}x$:

$$\begin{array}{cccc}x& 1& 3& 9\\ y& 0& 1& 2\end{array}$$

Сначала сдвигаем вправо:

$$x:1\to 2,3\to 4,9\to 10$$

Затем вверх:

$$y:0\to 1,1\to 2,2\to 3$$

Новая таблица:

$$\begin{array}{cccc}x& 2& 4& 10\\ y& 1& 2& 3\end{array}$$

Шаг 3: Область определения

$$x-1>0\Rightarrow x>1\Rightarrow D(x)=(1;+\mathrm{\infty })$$

Шаг 4: Значения

$$E(y)=(-\mathrm{\infty };+\mathrm{\infty })$$