ГДЗ по Алгебре 10-11 Класс Учебник 📕 Алимов — Все Части

Алгебра

10-11 класс учебник Алимов

10 класс

Тип

ГДЗ, Решебник.

Автор

Ш.А. Алимов, Ю.М. Колягин, М.В. Ткачева.

Год

2015-2024.

Издательство

Просвещение.

Описание

Учебник «Алгебра» для 10-11 классов под авторством Алимова – это один из наиболее популярных и широко используемых учебных пособий для старшеклассников. Он заслужил признание как среди учителей, так и среди учеников благодаря своей структурированности, доступности изложения и качественной проработке материала.

Учебник охватывает весь необходимый курс алгебры для 10-11 классов, включая такие сложные темы, как производные, интегралы, логарифмы и элементы математического анализа. Материал представлен последовательно и логично, что позволяет ученикам постепенно углубляться в изучение предмета. Пособие включает как теоретическую часть, так и большое количество практических заданий различного уровня сложности, что способствует закреплению знаний.

Одной из главных особенностей учебника является наличие задач повышенной сложности, которые стимулируют развитие логического мышления и навыков решения нестандартных задач. Кроме того, в книге представлены примеры из реальной жизни, что делает изучение алгебры более интересным и прикладным.

Преимущества учебника

Четкая структура материала
Учебник разделен на главы и параграфы с последовательным изложением тем. Это позволяет ученикам легко ориентироваться в содержании и возвращаться к ранее изученным темам для повторения.
Пошаговые объяснения
Каждая новая тема сопровождается подробными примерами с пошаговым решением. Это помогает ученикам лучше понять алгоритмы выполнения задач.
Разнообразие упражнений
В учебнике представлены задачи разного уровня сложности: от базовых до олимпиадных. Это делает пособие полезным как для обычных школьников, так и для тех, кто готовится к экзаменам или олимпиадам.
Практическая направленность
Включение задач из реальной жизни (например, расчет процентов или использование математических моделей) помогает ученикам видеть практическое применение алгебры.
Подготовка к ЕГЭ
Учебник содержит задания, аналогичные тем, которые встречаются на ЕГЭ, что делает его отличным инструментом для подготовки к экзаменам.

Учебник «Алгебра» Алимова для 10-11 классов – это надежный помощник в изучении математики. Он подходит как для базового освоения предмета, так и для углубленного изучения. Благодаря четкой структуре, разнообразию заданий и ориентации на экзамены, данный учебник является одним из лучших выборов для старшеклассников.

ГДЗ по Алгебре 10-11 Класс Номер 181 Алимов — Подробные Ответы

Задача

Изобразить график функции, обратной к функции, график которой представлен на рисунке 33.

Краткий ответ:

График обратной функции симметричен графику основной функции относительно прямой $y = x$ ;

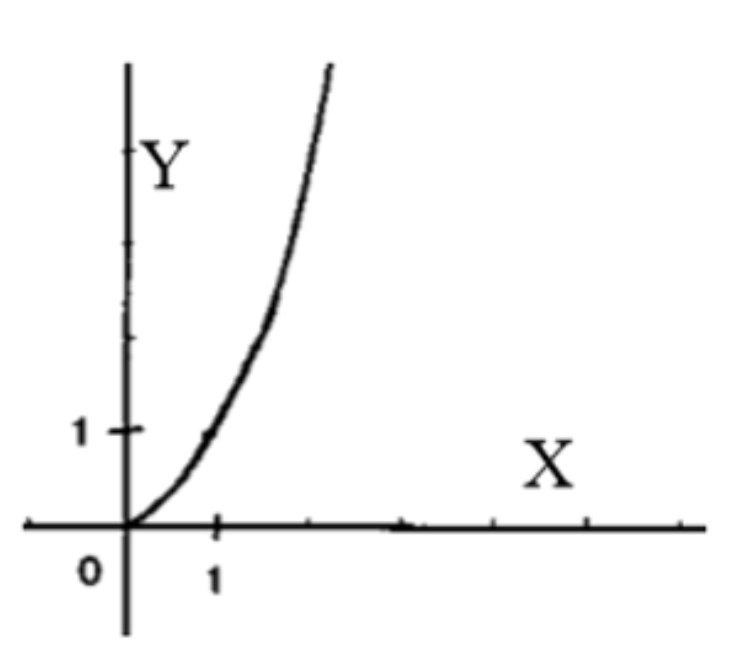
1). Рисунок 33 – а:

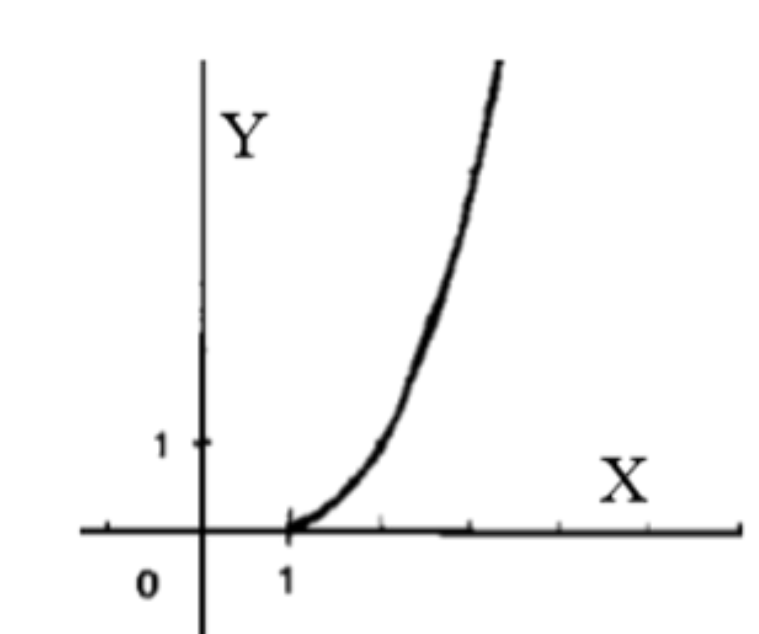
2). Рисунок 33 – б:

$\boxed{ \text{См. текст выше} }$

Подробный ответ:

В данной задаче требуется построить графики обратных функций и показать их симметричность относительно прямой $y = x$ .

Теоретическое обоснование

График обратной функции $y = f^{-1}(x)$ всегда является отражением графика исходной функции $y = f(x)$ $y = x$ . Это означает, что если точка $(a, b)$ принадлежит графику функции $y = f(x)$ , то точка $(b, a)$ обязательно принадлежит графику обратной функции $y = f^{-1}(x)$ .

Рассмотрение графиков

1) Рисунок 33 – а

На данном графике представлена функция $y = f(x)$ и её обратная функция $y = f^{-1}(x)$ , симметричные относительно прямой $y = x$ .

Прямая $y = x$ $проходит под углом 45° к осям координат и служит осью симметрии.$

Точки на графике исходной функции меняются местами при переходе к графику обратной функции:

Если ( $(a, b)$ принадлежит графику $y = f(x)$ , то $(b, a)$ принадлежит $y = f^{-1}(x)$ .

В результате график обратной функции получается отражением исходного относительно $y = x$ .

2) Рисунок 33 – б

Здесь также изображены два графика: один для функции $y = g(x)$ , а другой — для её обратной функции $y = g^{-1}(x)$ .

Оба графика симметричны относительно прямой $y = x$ .

Каждая точка ( $(a, b)$ на графике основной функции преобразуется в точку $(b, a)$ на графике обратной функции.

Визуально можно проследить, что графики действительно являются зеркальным отражением друг друга относительно линии $y = x$ .

Вывод

Графики обратных функций всегда являются зеркальным отражением графиков исходных функций относительно прямой $y = x$ . Данный принцип проиллюстрирован на обоих рисунках.

$\boxed{ \text{См. текст выше} }$

Оцени решение

← Предыдущий Следующий →

Сообщить об ошибке

Алгебра