ГДЗ по Алгебре 10-11 Класс Номер 162 Алимов — Подробные Ответы

Выяснить с помощью графиков, сколько корней имеет уравнение:

1. корень (x-6) = -x2;
2. корень 3 степени x = (x-1)2;
3. корень (x+1) = x2-7;
4. x3-1= корень (x+1).

1)$$\sqrt{x — 6} = -x^2;$$

$y = \sqrt{x — 6}$— уравнение ветви параболы:

$$x — 6 \geq 0 \quad \Rightarrow \quad x \geq 6 \quad \text{и} \quad y \geq 0;$$

$y = -x^2$— уравнение параболы:

$$x_0 = 0 \quad \text{и} \quad y_0 = -0^2 = 0;$$

Графики функций:

Ответ: корней нет.

2)$$\sqrt[3]{x} = (x — 1)^2;$$

$y = \sqrt[3]{x}$— уравнение кубической параболы:

$$x \in \mathbb{R} \quad \text{и} \quad y \in \mathbb{R};$$

$y = (x — 1)^2$— уравнение параболы:

$$x_0 — 1 = 0 \quad \Rightarrow \quad x_0 = 1 \quad \text{и} \quad y_0 = (1 — 1)^2 = 0;$$

Графики функций:

Ответ: два корня.

3)$$\sqrt{x + 1} = x^2 — 7;$$

$y = \sqrt{x + 1}$— уравнение ветви параболы:

$$x + 1 \geq 0 \quad \Rightarrow \quad x \geq -1 \quad \text{и} \quad y \geq 0;$$

$y = x^2 — 7$ — уравнение параболы:

$$x_0 = 0 \quad \text{и} \quad y_0 = 0^2 — 7 = -7;$$

Графики функций:

Ответ: один корень.

4)$$x^3 — 1 = \sqrt{x + 1};$$

$y = x^3 — 1$ — уравнение кубической параболы:

$$x \in \mathbb{R} \quad \text{и} \quad y \in \mathbb{R};$$

$y = \sqrt{x + 1}$— уравнение ветви параболы:

$$x + 1 \geq 0 \quad \Rightarrow \quad x \geq -1 \quad \text{и} \quad y \geq 0;$$

Графики функций:

Ответ: один корень.

1)
Уравнение:$$\sqrt{x — 6} = -x^2;$$

Исследуем функцию $y = \sqrt{x — 6}$:
Это уравнение ветви параболы. Чтобы значение под корнем было определено, нужно:

$$x — 6 \geq 0 \quad \Rightarrow \quad x \geq 6.$$

Таким образом, $x \geq 6$ и $y \geq 0$, так как корень из любого числа всегда неотрицателен.

Вычислим несколько значений для $y = \sqrt{x — 6}$:

• При $x=6$: $y = \sqrt{6 — 6} = 0$
• При $x=10$: $y = \sqrt{10 — 6} = \sqrt{4} = 2$
• При $x=22$: $y = \sqrt{22 — 6} = \sqrt{16} = 4$

Получаем таблицу значений:

Исследуем функцию $y = -x^2$:
Это уравнение параболы, открывающейся вниз. Для $x = 0$ имеем:

$$y_0 = -0^2 = 0.$$

Некоторые другие значения:

• При $x=-4$: $y = -(-4)^2 = -16$
• При $x=-2$: $y=-(-2{)}^2=-4$
• $y = -(-2)^2 = -4$При $x=2$: $y = -(2)^2 = -4$
• При $x=5$: $y = -(5)^2 = -16$

Получаем таблицу значений:

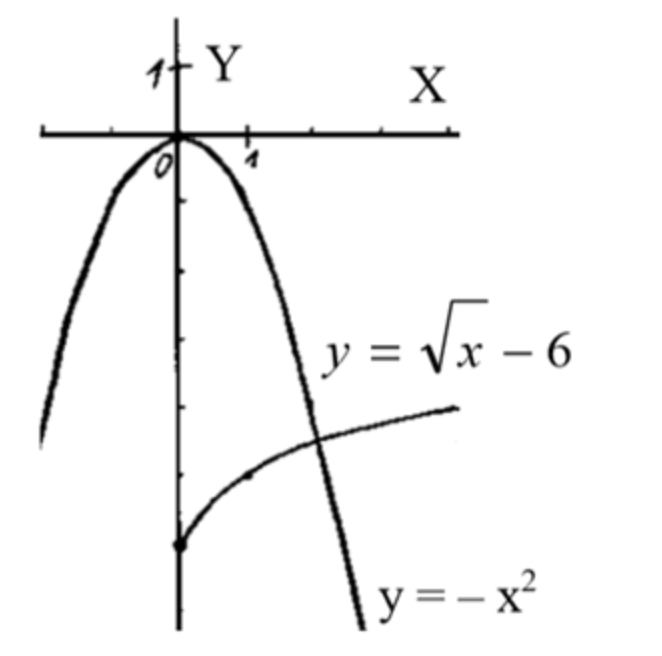
Графики функций:

• График $y=\sqrt{x-6}$является ветвью параболы, расположенной в правой части оси $x$, начиная с точки $(6,0).$$$
• График $y=-x^2$ — это обычная парабола, открывающаяся вниз, которая имеет значения ниже оси $x$ для всех $x\mathrm{\ne }0$.

Из графиков видно, что они не пересекаются. Это означает, что у уравнения нет решений.

Ответ: Корней нет.

2)
Уравнение:$$\sqrt[3]{x} = (x — 1)^2;$$

Исследуем функцию $y = \sqrt[3]{x}$:
Это кубическая парабола, которая определена для всех $x \in \mathbb{R}$. Важно заметить, что кубический корень существует для любых $x$.

Рассчитаем несколько значений:

• При $x=-8$: $y = \sqrt[3]{-8} = -2$
• При $x=-1$: $y = \sqrt[3]{-1} = -1$
• При $x=0$: $y = \sqrt[3]{0} = 0$
• При $x=1$: $y = \sqrt[3]{1} = 1$
• При $x=8$: $y = \sqrt[3]{8} = 2$

Получаем таблицу значений:

Исследуем функцию $y = (x — 1)^2$:
Это парабола, открывающаяся вверх. Для $x_0 = 1$ имеем:

$$y_0 = (1 — 1)^2 = 0.$$

Рассчитаем несколько других значений:

• При $x=-2$: $y = (-2 — 1)^2 = (-3)^2 = 9$
• При $x=-1$: $y = (-1 — 1)^2 = (-2)^2 = 4$
• При $x=1$: $y = (1 — 1)^2 = 0$
• При $x=2$: $y = (2 — 1)^2 = 1^2 = 1$
• При $x=3$: $y = (3 — 1)^2 = 2^2 = 4$
• При $x=4$: $y = (4 — 1)^2 = 3^2 = 9$

Получаем таблицу значений:

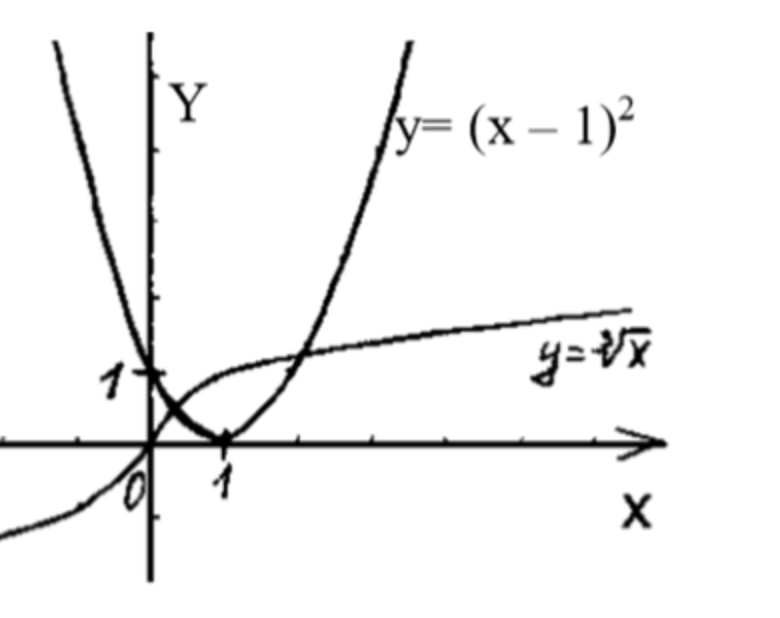
Графики функций:

• График $y=\sqrt[3]{x}$— это кубическая парабола, которая проходит через начало координат.
• График $y=(x-1{)}^2$— это парабола, которая открывается вверх и имеет минимум в точке $(1, 0)$

При пересечении этих графиков видно, что они пересекаются в двух точках: $x = 0$ и $x = 2$.

Ответ: Два корня.

3)
Уравнение:$$\sqrt{x + 1} = x^2 — 7;$$

Исследуем функцию $y = \sqrt{x + 1}$:
Это уравнение ветви параболы. Чтобы значение под корнем было определено, нужно:

$$x + 1 \geq 0 \quad \Rightarrow \quad x \geq -1.$$

Рассчитаем несколько значений:

• При $x=-1$: $y = \sqrt{-1 + 1} = 0$
• При $x=0$: $y = \sqrt{0 + 1} = 1$
• При $x=3$: $y = \sqrt{3 + 1} = \sqrt{4} = 2$
• При $x=8$: $y = \sqrt{8 + 1} = \sqrt{9} = 3$

Получаем таблицу значений:

Исследуем функцию $y = x^2 — 7$:
Это парабола, открывающаяся вверх. Для $x = 0$:

$$y_0 = 0^2 — 7 = -7.$$

Рассчитаем несколько значений:

• При $x=-3$: $y = (-3)^2 — 7 = 9 — 7 = 2$
• При $x=-2$: $y = (-2)^2 — 7 = 4 — 7 = -3$
• При $x=-1$: $y = (-1)^2 — 7 = 1 — 7 = -6$
• При $x=1$: $y = (1)^2 — 7 = 1 — 7 = -6$
• При $x=2$: $y = (2)^2 — 7 = 4 — 7 = -3$
• При $x=3$: $y = (3)^2 — 7 = 9 — 7 = 2$

Получаем таблицу значений:

Графики функций:

• График $y=\sqrt{x+1}$— это ветвь параболы, которая начинается с точки $(-1, 0)$ и растет вверх.
• График $y=x^2-7$— это парабола, открывающаяся вверх.

Графики пересекаются в одной точке, что подтверждается пересечением в $x = 3$.

Ответ: Один корень.

4)
Уравнение:$$x^3 — 1 = \sqrt{x + 1};$$

Исследуем функцию $y = x^3 — 1$:
Это кубическая парабола, определенная для всех $x \in \mathbb{R}$.

Рассчитаем несколько значений:

• При $x=-2$: $y = (-2)^3 — 1 = -8 — 1 = -9$
• При $x=-1$: $y = (-1)^3 — 1 = -1 — 1 = -2$
• При $x=0$: $y = (0)^3 — 1 = 0 — 1 = -1$
• При $x=1$: $y = (1)^3 — 1 = 1 — 1 = 0$
• При $x=2$: $y = (2)^3 — 1 = 8 — 1 = 7$

Получаем таблицу значений:

Исследуем функцию $y = \sqrt{x + 1}$:

Это ветвь параболы, определенная для $x \geq -1$.

Рассчитаем несколько значений:

• При $x=-1$: $y = \sqrt{-1 + 1} = 0$
• При $x=0$: $y = \sqrt{0 + 1} = 1$
• При $x=3$: $y = \sqrt{3 + 1} = \sqrt{4} = 2$
• При $x=8$:

$$y = \sqrt{8 + 1} = \sqrt{9} = 3$$

Получаем таблицу значений:

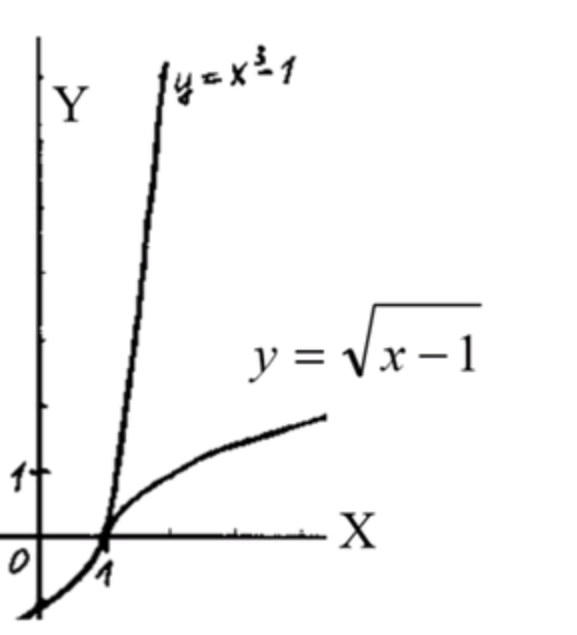
Графики функций:

• График $y=x^3-1$— это кубическая парабола.
• График $y=\sqrt{x+1}$— это ветвь параболы, которая начинается в точке $(-1, 0)$.

Графики пересекаются в одной точке.

Ответ: Один корень.

Итоговые ответы:

1. Корней нет.
2. Два корня.
3. Один корень.
4. Один корень.