ГДЗ по Алгебре 10-11 Класс Номер 1164 Алимов — Подробные Ответы
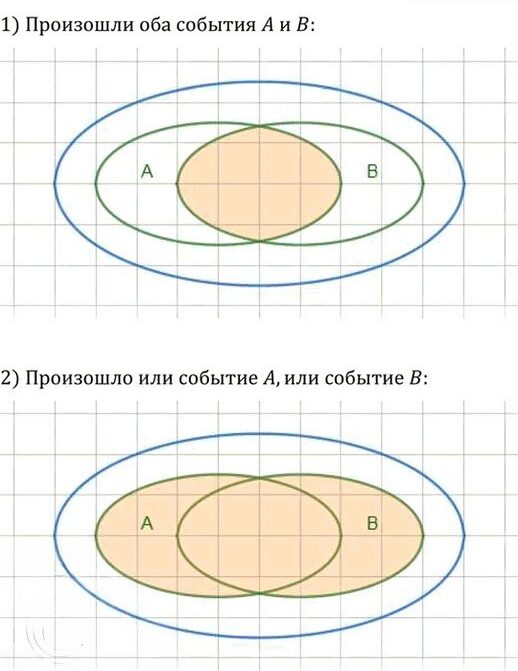
События А и В изображены с помощью кругов Эйлера (рис. 172). Большим кругом изображены все элементарные исходы испытания, с которым связаны события А и В. Перенести рисунок в тетрадь и штриховкой показать событие, состоящее в том, что: 1) произошли оба события А и В; 2) произошло или событие А9 или событие В; 3) произошло только событие А; 4) произошло событие В.
1. Произошли оба события A и B
Когда происходит одновременное событие A и событие B, это означает, что мы рассматриваем пересечение двух множеств A и B. На круге Эйлера это изображается как пересекающаяся область двух кругов. Для этого нужно заштриховать только ту область, где круги A и B пересекаются.
Если представить круги Эйлера, то пересечение будет в центре, там, где оба круга налегают друг на друга. Таким образом, штриховка будет именно в этой области.
2. Произошло или событие A, или событие B
Если произошло событие A или событие B, это подразумевает объединение этих двух событий, то есть любой исход, который попадает хотя бы в одно из этих событий. В круге Эйлера это будет вся область, которая охватывается хотя бы одним из кругов (A или B), включая их пересечение.
Штриховка должна покрывать все пространство, которое охватывается двумя кругами. То есть, если оба круга пересекаются, то штриховать нужно всю область кругов, включая их пересечение и внешние части каждого из них.
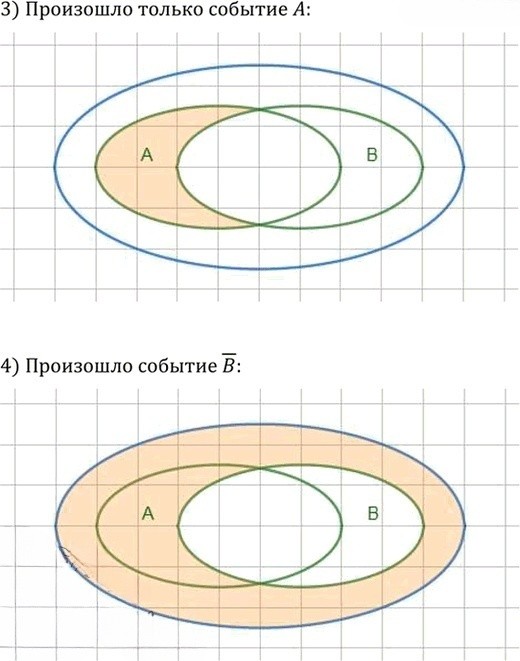
3. Произошло только событие A
Когда произошло только событие A, это значит, что мы рассматриваем событие A без события B. В круге Эйлера это будет та часть круга A, которая не пересекается с кругом B. Мы штрихуем только ту область, которая находится внутри круга A, но не входит в пересечение с кругом B.
Иными словами, это будет левая часть круга A, которая не касается области B. В этой части происходит только событие A, и не происходит событие B.
4. Произошло событие B
Когда произошло событие B, мы должны заштриховать всю область круга B. Это включает как часть, которая пересекается с A, так и часть, которая не пересекается с A.
То есть, в круге Эйлера это будет весь круг B (включая пересечение с A). Мы не затрагиваем круг A в этой задаче, а только область B.
