ГДЗ по Алгебре 10-11 Класс Номер 1020 Алимов — Подробные Ответы

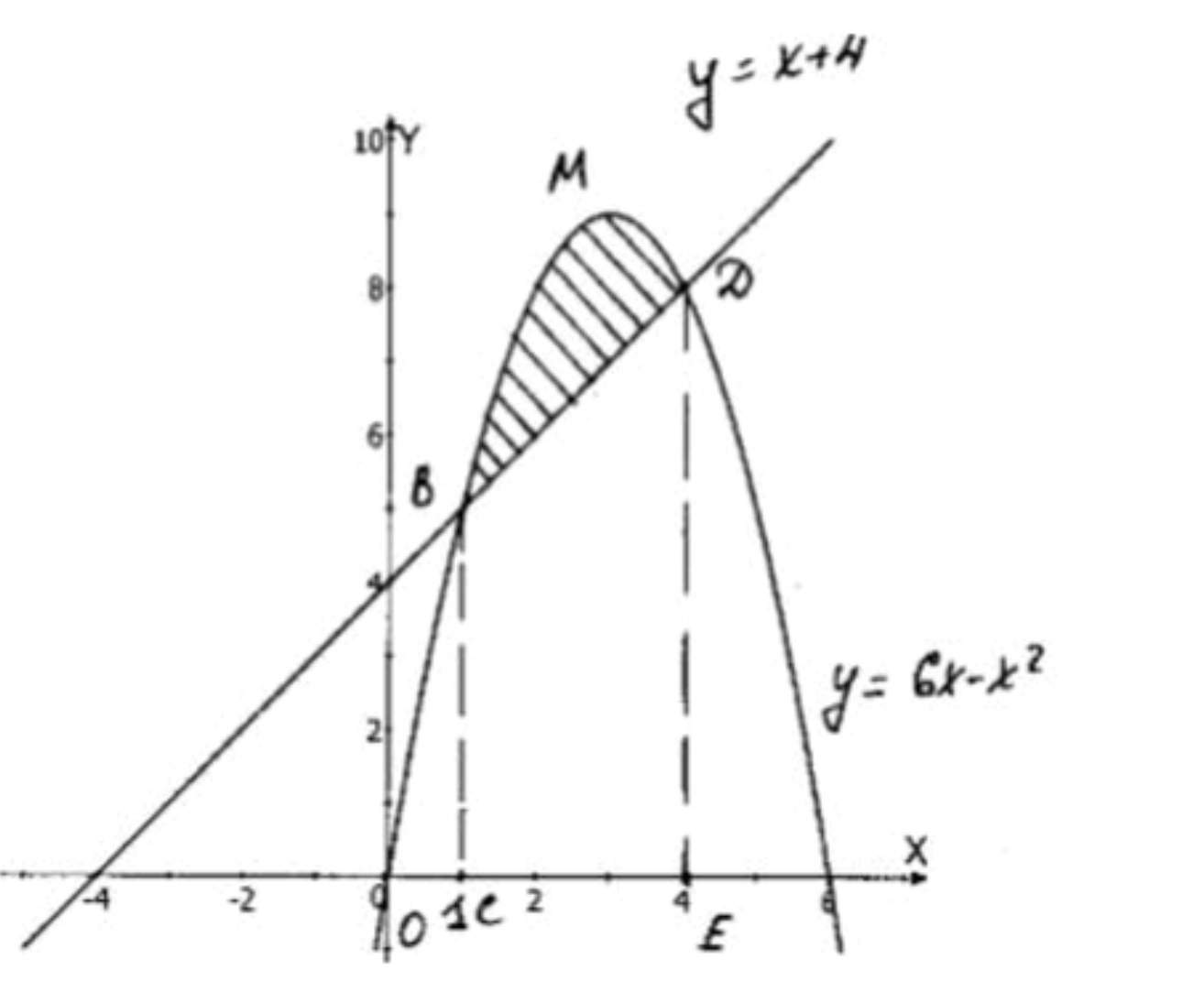
1. параболой у = 6х — х2 и прямой у = х + 4;
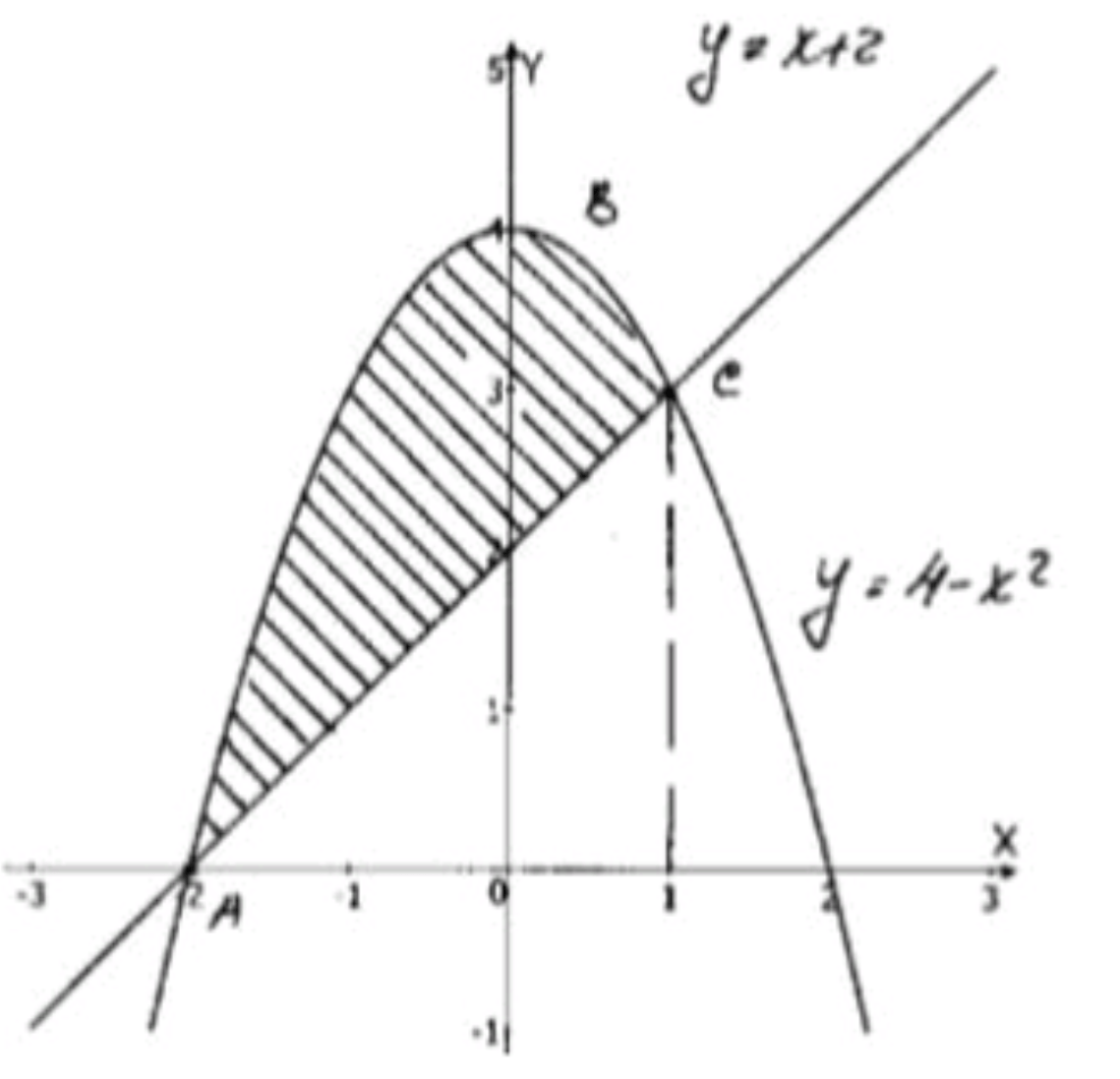
2. параболой у = 4 — х2 и прямой у = х + 2.

1) $y=6x-x^2$ и $y=x+4$

Точки пересечения функций:

$$6x-x^2=x+4$$$$x^2+x-6x+4=0$$$$x^2-5x+4=0$$$$D=5^2-4\cdot 4=25-16=9$$

Тогда:

$$x_1=\frac{5-3}{2}=1\text{и}{x}_2=\frac{5+3}{2}=4$$

Площадь криволинейной трапеции:

$$S={\int }_1^4((6x-x^2)-(x+4))dx$$$$={\int }_1^4(6x-x^2-x-4)dx$$$$={\int }_1^4(5x-x^2-4)dx$$$$={[\frac{5x^2}{2}-\frac{x^3}{3}-4x]}_1^4$$$$=(\frac{5\cdot 4^2}{2}-\frac{4^3}{3}-4\cdot 4)-(\frac{5\cdot 1^2}{2}-\frac{1^3}{3}-4\cdot 1)$$$$=(\frac{80}{2}-\frac{64}{3}-16)-(\frac{5}{2}-\frac{1}{3}-4)$$$$=(40-\frac{64}{3}-16)-(\frac{5}{2}-\frac{1}{3}-4)$$$$=(24-\frac{64}{3})-(\frac{5}{2}-\frac{1}{3}-4)$$$$=(\frac{72}{3}-\frac{64}{3})-(\frac{15}{6}-\frac{2}{6}-\frac{24}{6})$$$$=\frac{8}{3}-\left(\frac{15-2-24}{6}\right)$$$$=\frac{8}{3}-\left(\frac{-11}{6}\right)$$$$=\frac{8}{3}+\frac{11}{6}$$$$=\frac{16}{6}+\frac{11}{6}$$$$=\frac{27}{6}$$$$=4.5$$

Ответ: $4.5$

2) $y=4-x^2$ и $y=x+2$

Точки пересечения функций:

$$4-x^2=x+2$$$$x^2+x+2-4=0$$$$x^2+x-2=0$$$$D=1^2+4\cdot 2=1+8=9$$

Тогда:

$$x_1=\frac{-1-3}{2}=-2\text{и}{x}_2=\frac{-1+3}{2}=1$$

Площадь криволинейной трапеции:

$$S={\int }_{-2}^1((4-x^2)-(x+2))dx$$$$={\int }_{-2}^1(4-x^2-x-2)dx$$$$={\int }_{-2}^1(2-x^2-x)dx$$$$={[2x-\frac{x^3}{3}-\frac{x^2}{2}]}_{-2}^1$$$$=(2\cdot 1-\frac{1^3}{3}-\frac{1^2}{2})-(2\cdot (-2)-\frac{(-2{)}^3}{3}-\frac{(-2{)}^2}{2})$$$$=(2-\frac{1}{3}-\frac{1}{2})-(-4+\frac{8}{3}-2)$$$$=(2-\frac{1}{3}-\frac{1}{2})-(-6+\frac{8}{3})$$$$=(\frac{12}{6}-\frac{2}{6}-\frac{3}{6})-(-\frac{18}{3}+\frac{8}{3})$$$$=\left(\frac{7}{6}\right)-(-\frac{10}{3})$$$$=\frac{7}{6}+\frac{20}{6}$$$$=\frac{27}{6}$$$$=4.5$$

Ответ: $4.5$

1) $y=6x-x^2$ и $y=x+4$

Нужно найти точки пересечения функций и затем вычислить площадь криволинейной трапеции.

1.1) Точки пересечения

Для нахождения точек пересечения приравняем обе функции:

$$6x-x^2=x+4$$

Приводим все слагаемые на одну сторону:

$$6x-x^2-x-4=0$$

Упростим:

$$-x^2+5x-4=0$$

Умножим обе части на $-1$ для удобства:

$$x^2-5x+4=0$$

Решим это квадратное уравнение с помощью формулы дискриминанта.

Дискриминант:

$$D=(-5{)}^2-4\cdot 1\cdot 4=25-16=9$$

Теперь найдем корни уравнения:

$$x_1=\frac{-(-5)-\sqrt{9}}{2\cdot 1}=\frac{5-3}{2}=1$$$$x_2=\frac{-(-5)+\sqrt{9}}{2\cdot 1}=\frac{5+3}{2}=4$$

Итак, точки пересечения: $x_1=1$ и $x_2=4$.

1.2) Площадь криволинейной трапеции

Теперь, чтобы найти площадь, нужно вычислить интеграл разности функций $y=6x-x^2$ и $y=x+4$ на интервале от $x_1=1$ до $x_2=4$:

$$S={\int }_1^4((6x-x^2)-(x+4))dx$$

Упростим подынтегральное выражение:

$$S={\int }_1^4(6x-x^2-x-4)dx$$$$S={\int }_1^4(5x-x^2-4)dx$$

Теперь интегрируем по частям:

$$S={[\frac{5x^2}{2}-\frac{x^3}{3}-4x]}_1^4$$

Подставляем верхний предел $x=4$:

$$\frac{5\cdot 4^2}{2}-\frac{4^3}{3}-4\cdot 4=\frac{80}{2}-\frac{64}{3}-16=40-\frac{64}{3}-16=24-\frac{64}{3}$$

Подставляем нижний предел $x=1$:

$$\frac{5\cdot 1^2}{2}-\frac{1^3}{3}-4\cdot 1=\frac{5}{2}-\frac{1}{3}-4=\frac{5}{2}-\frac{1}{3}-\frac{12}{3}=\frac{5}{2}-\frac{13}{3}$$

Теперь, вычитаем результаты:

$$S=(24-\frac{64}{3})-(\frac{5}{2}-\frac{13}{3})$$

Для упрощения выражений приведи дроби к общему знаменателю. Преобразуем в общий знаменатель для каждой из разностей.

Для первой разности $(24-\frac{64}{3})$:

$$24=\frac{72}{3}\Rightarrow 24-\frac{64}{3}=\frac{72}{3}-\frac{64}{3}=\frac{8}{3}$$

Для второй разности $(\frac{5}{2}-\frac{13}{3})$:

$$\frac{5}{2}=\frac{15}{6},\frac{13}{3}=\frac{26}{6}\Rightarrow \frac{5}{2}-\frac{13}{3}=\frac{15}{6}-\frac{26}{6}=\frac{-11}{6}$$

Теперь вычитаем:

$$S=\frac{8}{3}-\left(\frac{-11}{6}\right)=\frac{8}{3}+\frac{11}{6}$$

Приведем к общему знаменателю:

$$\frac{8}{3}=\frac{16}{6}\Rightarrow \frac{16}{6}+\frac{11}{6}=\frac{27}{6}=4.5$$

Ответ: $S=4.5$.

2) $y=4-x^2$ и $y=x+2$

Аналогично предыдущей задаче.

2.1) Точки пересечения

Приравниваем функции:

$$4-x^2=x+2$$

Переносим все на одну сторону:

$$-x^2-x+4-2=0\Rightarrow x^2+x-2=0$$

Находим дискриминант:

$$D=1^2-4\cdot 1\cdot (-2)=1+8=9$$

Корни уравнения:

$$x_1=\frac{-1-3}{2}=-2\text{и}{x}_2=\frac{-1+3}{2}=1$$

Точки пересечения: $x_1=-2$ и $x_2=1$.

2.2) Площадь криволинейной трапеции

Вычисляем площадь:

$$S={\int }_{-2}^1((4-x^2)-(x+2))dx$$

Упростим подынтегральное выражение:

$$S={\int }_{-2}^1(4-x^2-x-2)dx={\int }_{-2}^1(2-x^2-x)dx$$

Интегрируем:

$$S={[2x-\frac{x^3}{3}-\frac{x^2}{2}]}_{-2}^1$$

Подставляем верхний предел $x=1$:

$$S_1=2\cdot 1-\frac{1^3}{3}-\frac{1^2}{2}=2-\frac{1}{3}-\frac{1}{2}=\frac{12}{6}-\frac{2}{6}-\frac{3}{6}=\frac{7}{6}$$

Подставляем нижний предел $x=-2$:

$$S_2=2\cdot (-2)-\frac{(-2{)}^3}{3}-\frac{(-2{)}^2}{2}=-4-\frac{-8}{3}-\frac{4}{2}=-4+\frac{8}{3}-2=$$

$$=-6+\frac{8}{3}=\frac{-18}{3}+\frac{8}{3}=\frac{-10}{3}$$

Теперь вычитаем:

$$S=\frac{7}{6}-\left(\frac{-10}{3}\right)=\frac{7}{6}+\frac{20}{6}=\frac{27}{6}=4.5$$

Ответ: $S=4.5$.

Ответы:

1. $\boxed{{\displaystyle 4.5}}$
2. $\boxed{{\displaystyle 4.5}}$