ГДЗ по Алгебре 10-11 Класс Номер 999 Алимов — Подробные Ответы

Изобразить криволинейную трапецию, ограниченную:

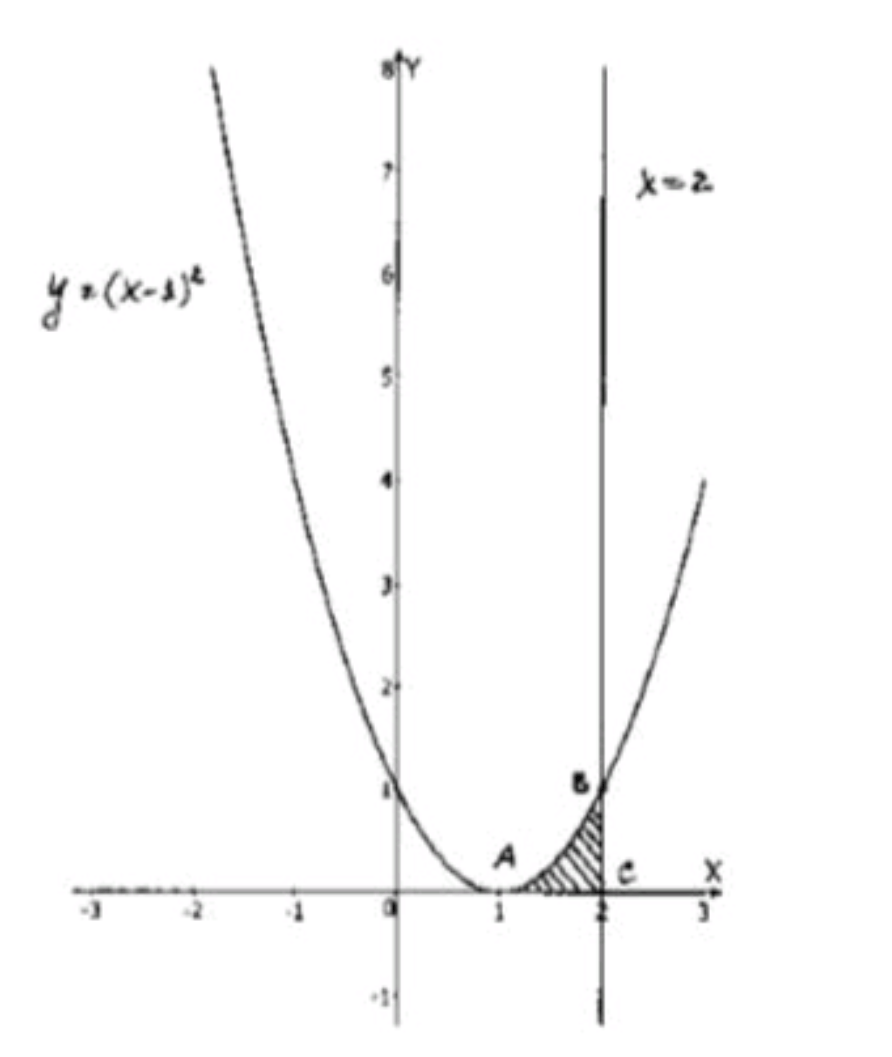
1. графиком функции у = (х — 1)2, осью Ох и прямой х = 2;
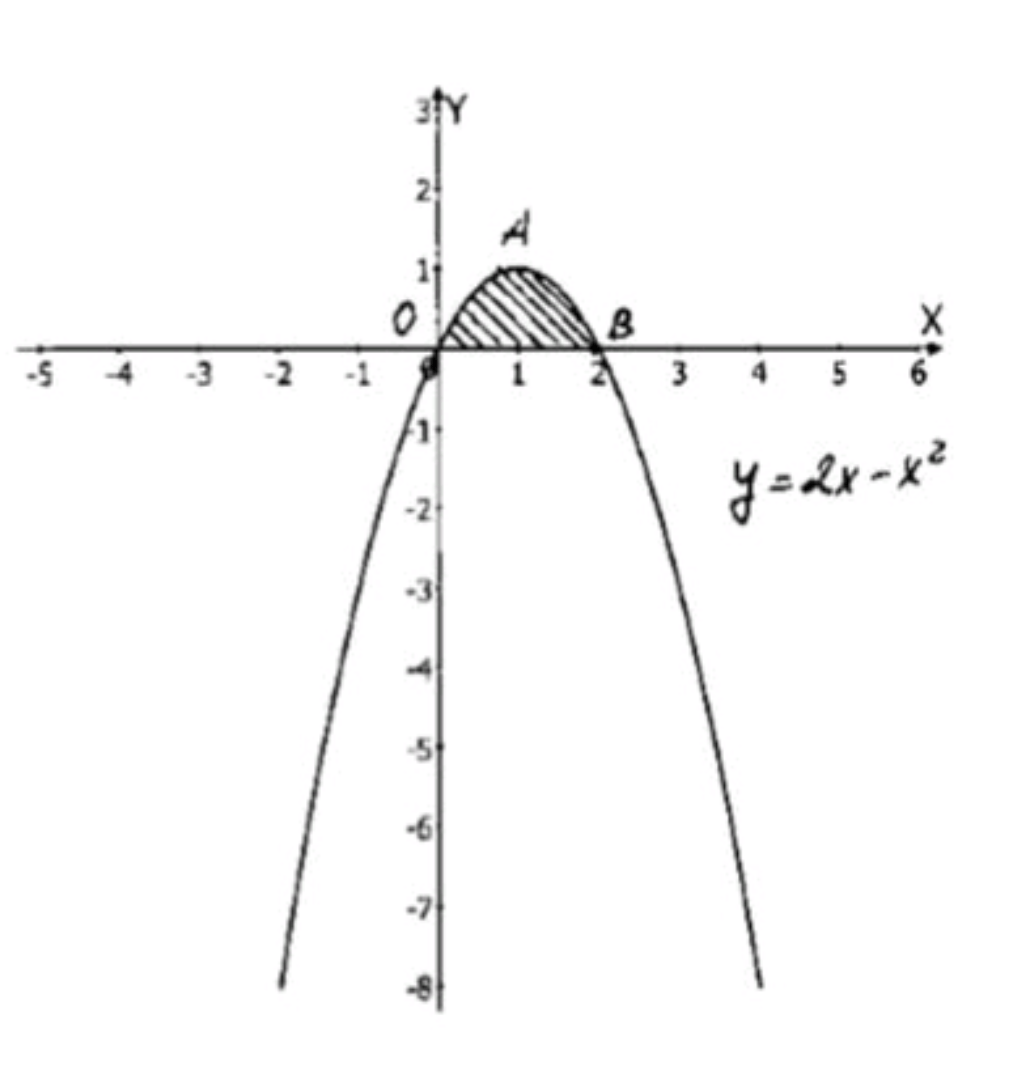
2. графиком функции у — 2х — х2 и осью Ох;
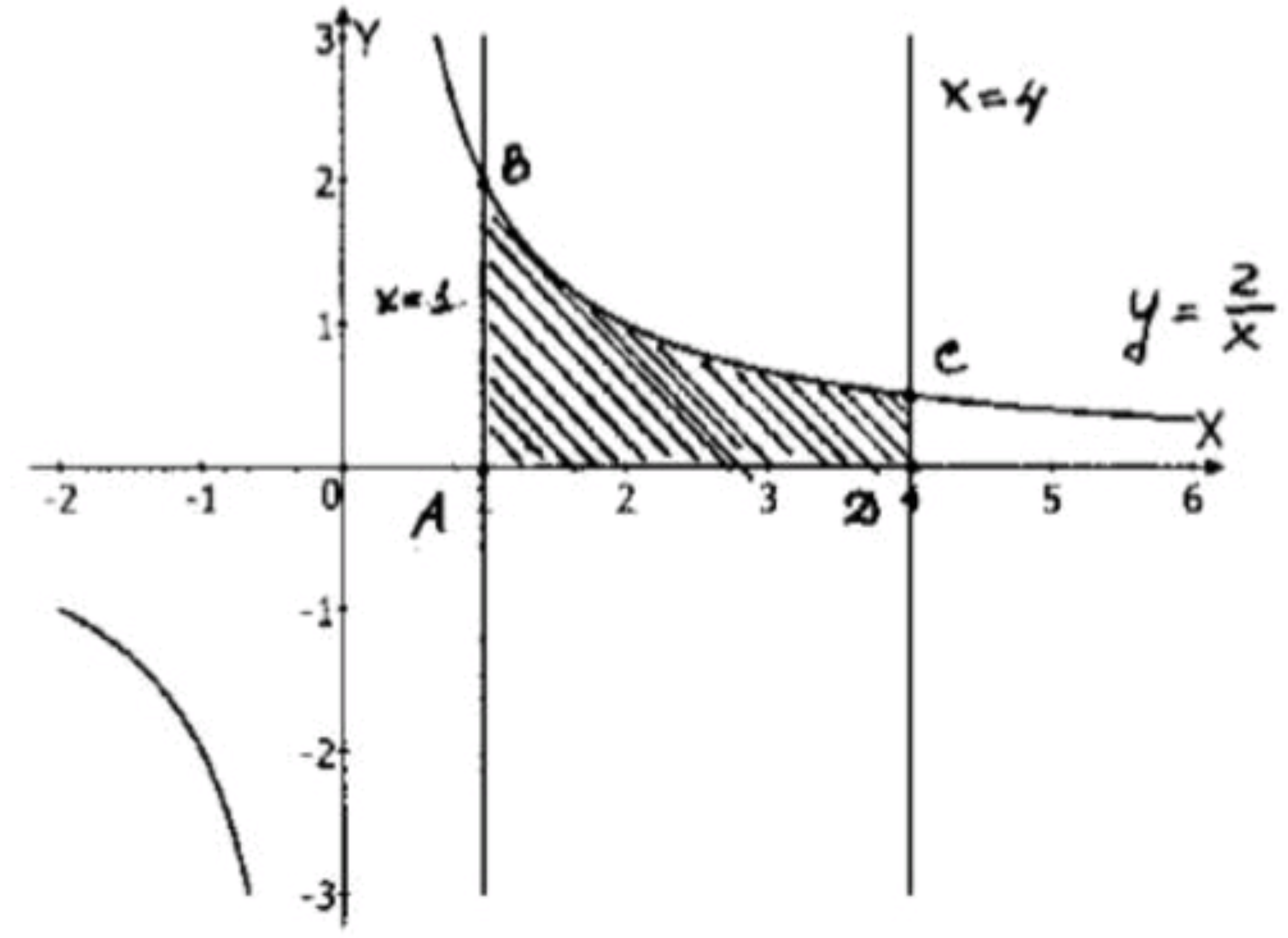
3. графиком функции у = 2/x, осью Ох и прямыми х=1, х = 4;
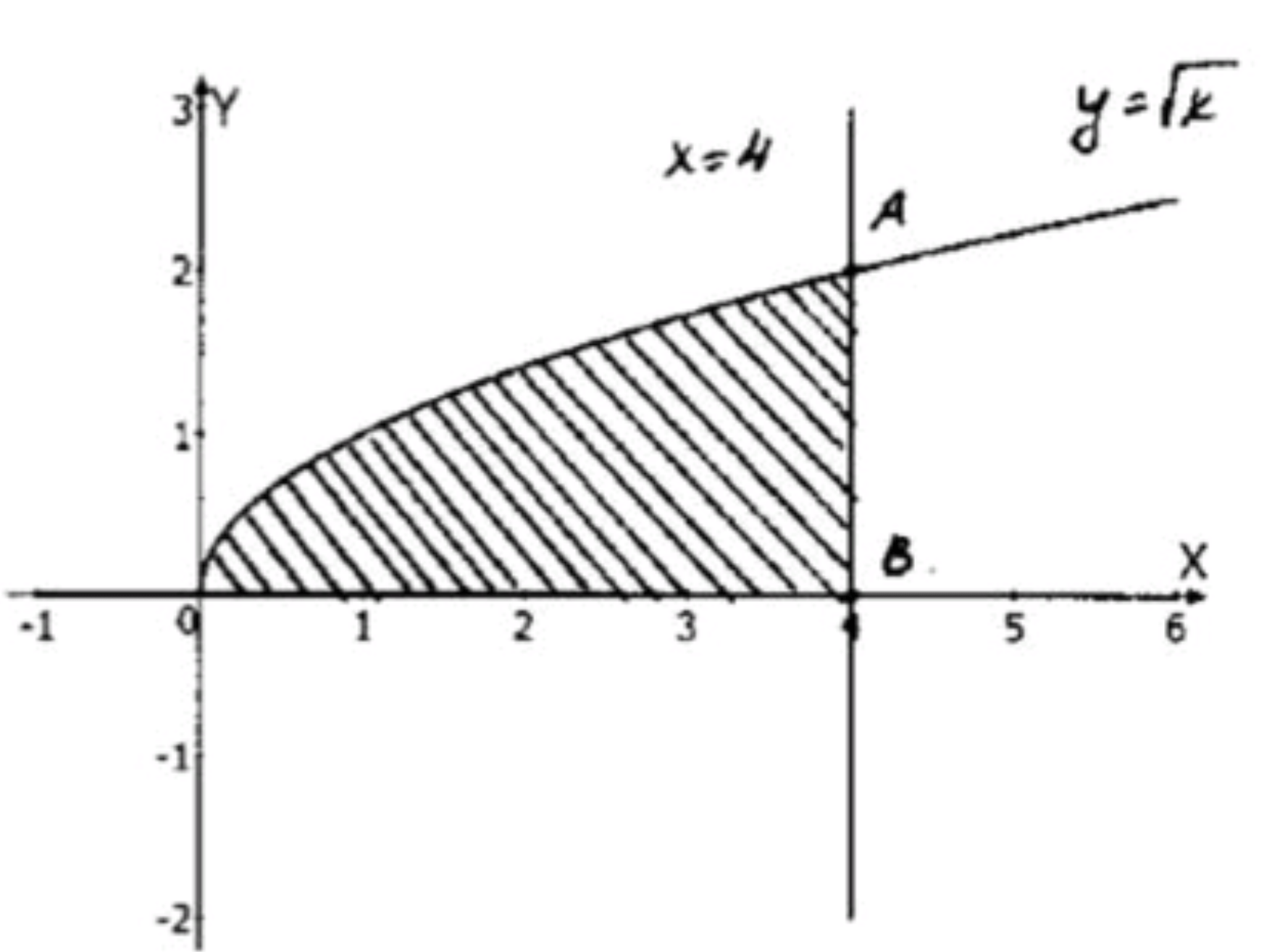
4. графиком функции у = корень х, осью Ох и прямой х = 4.

1) Изобразим криволинейную трапецию, ограниченную графиком функции $y = (x-1)^2$, осью $Ox$ и прямой $x = 2$.

Решение:

2) Изобразим криволинейную трапецию, ограниченную графиком функции $y = 2x — x^2$, осью $Ox$.

Решение:

3) Изобразим криволинейную трапецию, ограниченную графиком функции $y = \frac{2}{x}$, осью $Ox$ и прямыми $x = 1$, $x = 4$.

Решение:

4) Изобразим криволинейную трапецию, ограниченную графиком функции $y = \sqrt{x}$, осью $Ox$ и прямой $x = 4$.

Решение:

1. График функции $y = (x — 1)^2$, ограниченный осью $O_x$ и прямой $x = 2$:

Функция $y = (x — 1)^2$ является параболой, с вершиной в точке $(1, 0)$, которая открывается вверх. Мы будем ограничены осью $O_x$ (то есть, областью $y \geq 0$) и вертикальной прямой $x = 2$.

Шаги решения:

Определим, где график функции пересекает ось $O_x$. Для этого приравняем $y = 0$:

$$(x — 1)^2 = 0 \Rightarrow x = 1$$

Таким образом, график пересекает ось $O_x$ в точке $(1, 0)$.

Для прямой $x = 2$, подставим в уравнение $y = (x — 1)^2$:

$$y = (2 — 1)^2 = 1$$

Таким образом, точка пересечения графика функции с прямой $x = 2$ будет $(2, 1)$.

Таким образом, криволинейная трапеция будет ограничена графиком параболы, осью $O_x$ и прямой $x = 2$, от точки $(1, 0)$ до точки $(2, 0)$, с верхней частью, находящейся между точками $(1, 0)$ и $(2, 1)$.

2. График функции $y = 2x — x^2$, ограниченный осью $O_x$:

Функция $y = 2x — x^2$ представляет собой параболу, которая открывается вниз. Она будет пересекаться с осью $O_x$, когда $y = 0$:

$$2x — x^2 = 0 \Rightarrow x(2 — x) = 0$$

Это дает корни $x = 0$ и $x = 2$. Таким образом, график пересекает ось $O_x$ в точках $(0, 0)$ и $(2, 0)$.

Парабола имеет вершину в точке $x = 1$, где производная функции равна нулю:

$$\frac{d}{dx}(2x — x^2) = 2 — 2x \Rightarrow x = 1$$

При подстановке $x = 1$ в уравнение функции:

$$y = 2(1) — (1)^2 = 1$$

Таким образом, вершина параболы находится в точке $(1, 1)$. Криволинейная трапеция будет ограничена графиком функции, осью $O_x$ и прямыми $x = 0$ и $x = 2$.

3. График функции $y = \frac{2}{x}$, ограниченный осью $O_x$ и прямыми $x = 1$ и $x = 4$:

График функции $y = \frac{2}{x}$ — это гипербола, которая асимптотически стремится к осям $O_x$ и $O_y$, но никогда их не пересекает. Мы ограничиваем область графиком, прямыми $x = 1$ и $x = 4$, а также осью $O_x$.

Шаги решения:

Для $x = 1$, подставляем в уравнение:

$$y = \frac{2}{1} = 2$$

Таким образом, точка пересечения графика с прямой $x = 1$ — это $(1, 2)$.

Для $x = 4$, подставляем в уравнение:

$$y = \frac{2}{4} = 0.5$$

Таким образом, точка пересечения графика с прямой $x = 4$ — это $(4, 0.5)$.

Криволинейная трапеция будет ограничена графиком гиперболы, прямыми $x = 1$ и $x = 4$, а также осью $O_x$, между точками $(1, 2)$ и $(4, 0.5)$.

4. График функции $y = \sqrt{x}$, ограниченный осью $O_x$ и прямой $x = 4$:

Функция $y = \sqrt{x}$ — это парабола, которая открывается вправо. График пересекает ось $O_x$ в точке $(0, 0)$ и имеет точку $(4, 2)$, так как:

$$y = \sqrt{4} = 2$$

Таким образом, криволинейная трапеция будет ограничена графиком функции, осью $O_x$ и прямой $x = 4$, между точками $(0, 0)$ и $(4, 2)$.