ГДЗ по Алгебре 10-11 Класс Номер 981 Алимов — Подробные Ответы

Построить график функции:

1. y = (x2 — 1) корень (x+1);
2. у = |х| * корень 3 степени (1+3x);
3. у = x2e^-x;
4. у = x3е^-х.

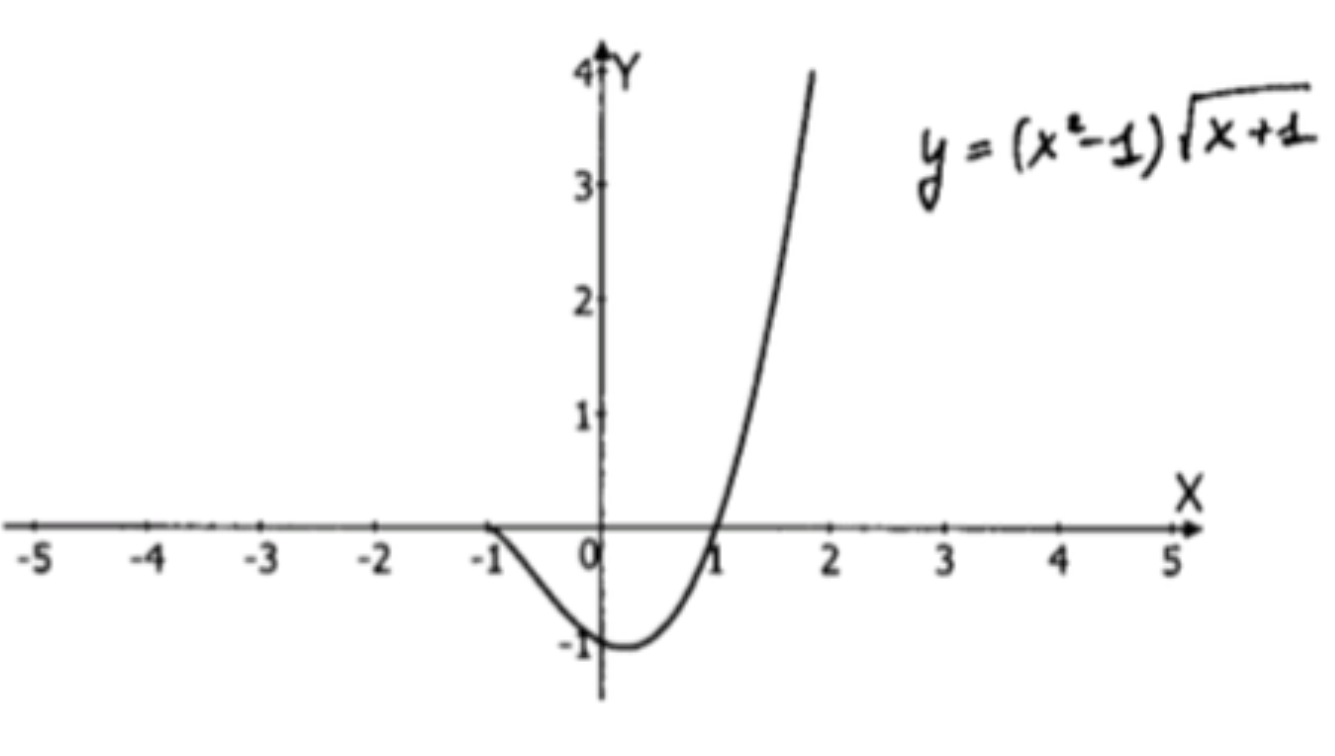
$y = (x^2 — 1) \cdot \sqrt{x + 1}$;

а) Область определения:

$$D(x) = (-1; +\infty);$$

б) Производная функции:

$$y^{\mathrm{\prime }}(x)=(x^2-1)\cdot \sqrt{x+1}+(x^2-1)\cdot (x+1{)}^{1\mathrm{/}2}$$
$$y'(x) = 2x \cdot \sqrt{x + 1} + (x^2 — 1) \cdot \frac{1}{2} \cdot (x + 1)^{-1/2};$$ $$y'(x) = 2x \cdot \sqrt{x + 1} + \frac{x^2 — 1}{2 \sqrt{x + 1}};$$ $$y'(x) = \frac{4x \cdot (x + 1) + x^2 — 1}{2 \sqrt{x + 1}};$$ $$y'(x) = \frac{5x^2 + 4x — 1}{2 \sqrt{x + 1}}.$$

в) Стационарные точки:

$$5x^2 + 4x — 1 = 0;$$

Дискриминант: $D = 4^2 — 4 \cdot 5 \cdot (-1) = 16 + 20 = 36$, тогда:

$$x_1 = \frac{-4 — 6}{2 \cdot 5} = -1 \quad \text{и} \quad x_2 = \frac{-4 + 6}{2 \cdot 5} = \frac{2}{10} = 0.2;$$

г) Значения функции:

$$f(-1) = ((-1)^2 — 1) \cdot \sqrt{-1 + 1} = (1 — 1) \cdot \sqrt{0} = 0;$$ $$f(0,2) = (0,2^2 — 1) \cdot \sqrt{0,2 + 1} = (0,04 — 1) \cdot \sqrt{1,2} \approx -1;$$

д) Промежутки монотонности:
Возрастает на $(0,2; +\infty)$ и убывает на $(-1; 0,2)$;
$x = 0,2$ — точка минимума.

е) Таблица свойств функции:

$$\begin{array}{|c|c|c|c|c|} \hline x & -1 < x < 0,2 & 0,2 & 0,2 < x < +\infty \\ \hline f'(x) & — & 0 & + \\ \hline f(x) & 0 & \downarrow & 1 \\ \hline \end{array}$$

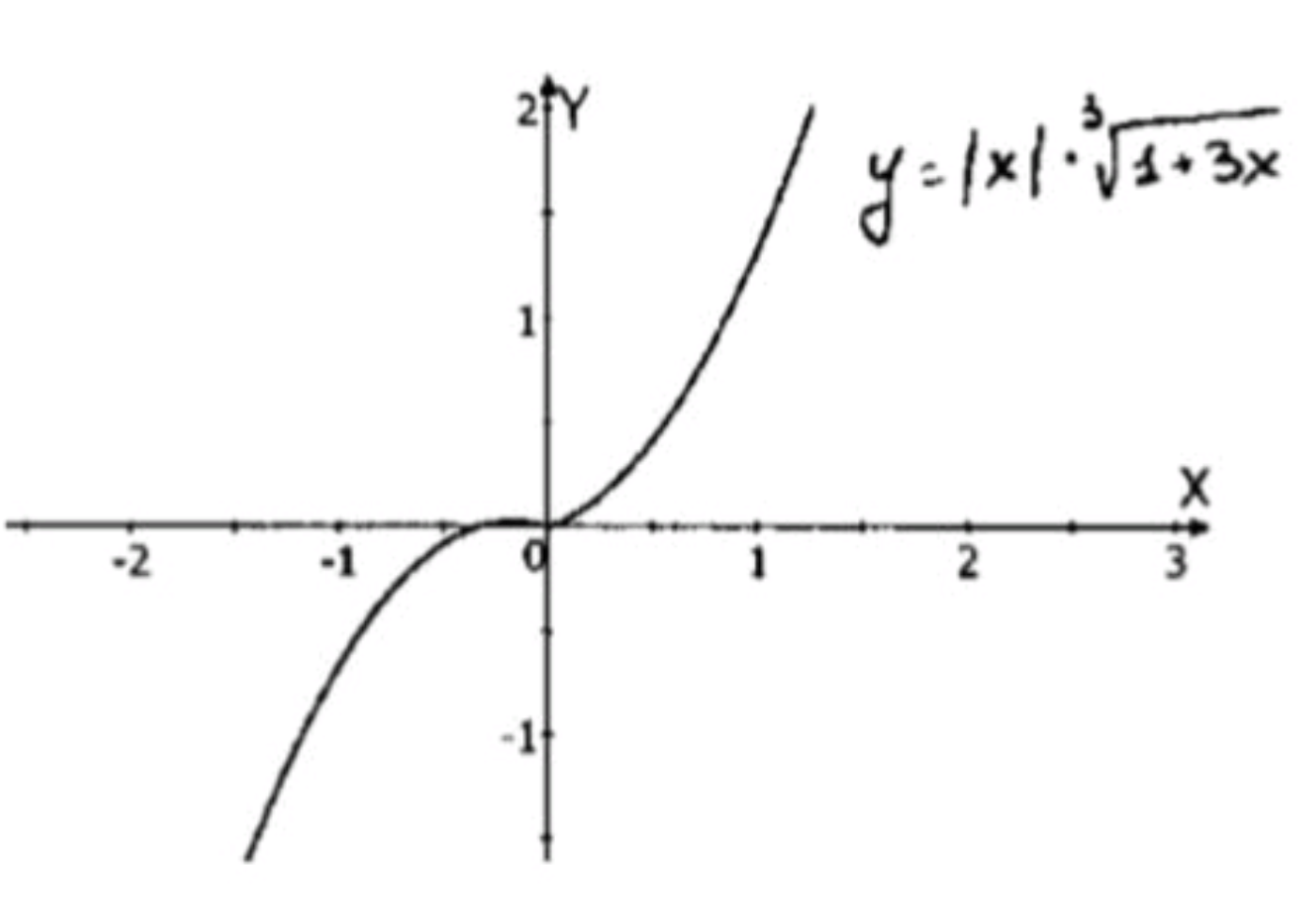
2) $y = |x| \cdot \sqrt{1 + 3x}$;

а) Область определения:

$$D(x) = (-\infty; +\infty);$$

б) Производная функции:

$$y^{\mathrm{\prime }}(x)=\pm (x)\cdot \sqrt{1+3x}+(\mathrm{\mid }x\mathrm{\mid })\cdot (1+3x{)}^{1\mathrm{/}3}$$
$$y'(x) = \pm \sqrt{1 + 3x} + \frac{x}{3 \cdot (1 + 3x)^{2/3}};$$

в) Стационарные точки:

$$\pm 3 \cdot (1 + 3x) + \frac{x}{3 \cdot (1 + 3x)^2};$$ $$\text{Точки: } x = -0,3.$$

г) Значения функции:

$$f(-1) = |(-1)| \cdot \sqrt{1 — 3} = \sqrt{0.1};$$ $$f(0) = 0.$$

д) Промежутки монотонности:
Возрастает на $(-\infty; -0,3) \cup (0; +\infty)$ и убывает на $(-0,3; 0)$.

е) Таблица свойств функции:

$$\begin{array}{|c|c|c|c|c|} \hline x & x < -0,3 & -0,3 & -0,3 < x < 0 & 0 \\ \hline f'(x) & + & 0 & — & 0 \\ \hline f(x) & \uparrow & 0 & \downarrow & 0 \\ \hline \end{array}$$

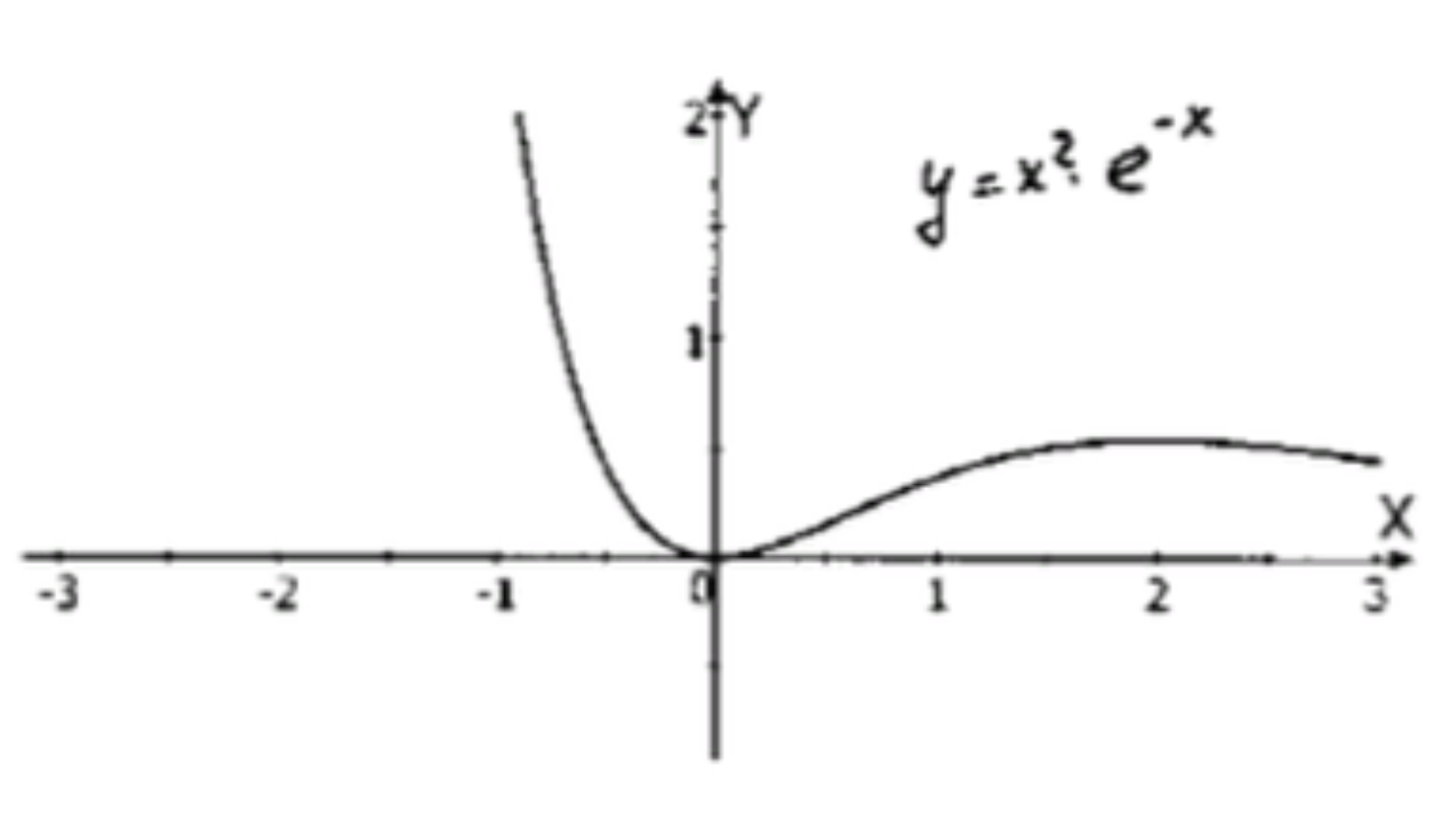
3) $y = x^2 \cdot e^{-x};$

а) Область определения:

$$D(x) = (-\infty; +\infty);$$

б) Производная функции:

$$y'(x) = (x^2)’ \cdot e^{-x} + x^2 \cdot (e^{-x})’;$$ $$y'(x) = 2x \cdot e^{-x} — x^2 \cdot e^{-x};$$ $$y'(x) = e^{-x} \cdot (2x — x^2).$$

в) Стационарные точки:

$$2x — x^2 = 0;$$ $$x(2 — x) = 0;$$ $$x_1 = 0 \quad \text{и} \quad x_2 = 2;$$

г) Значения функции:

$$f(0) = 0^2 \cdot e^{0} = 0;$$ $$f(2) = 2^2 \cdot e^{-2} = \frac{4}{e^2}.$$

д) Уравнение горизонтальной асимптоты:

$$y = \lim_{x \to \infty} x^2 \cdot e^{-x} = 0.$$

е) Промежутки монотонности:
Возрастает на $(0; 2)$ и убывает на $(2; +\infty)$.

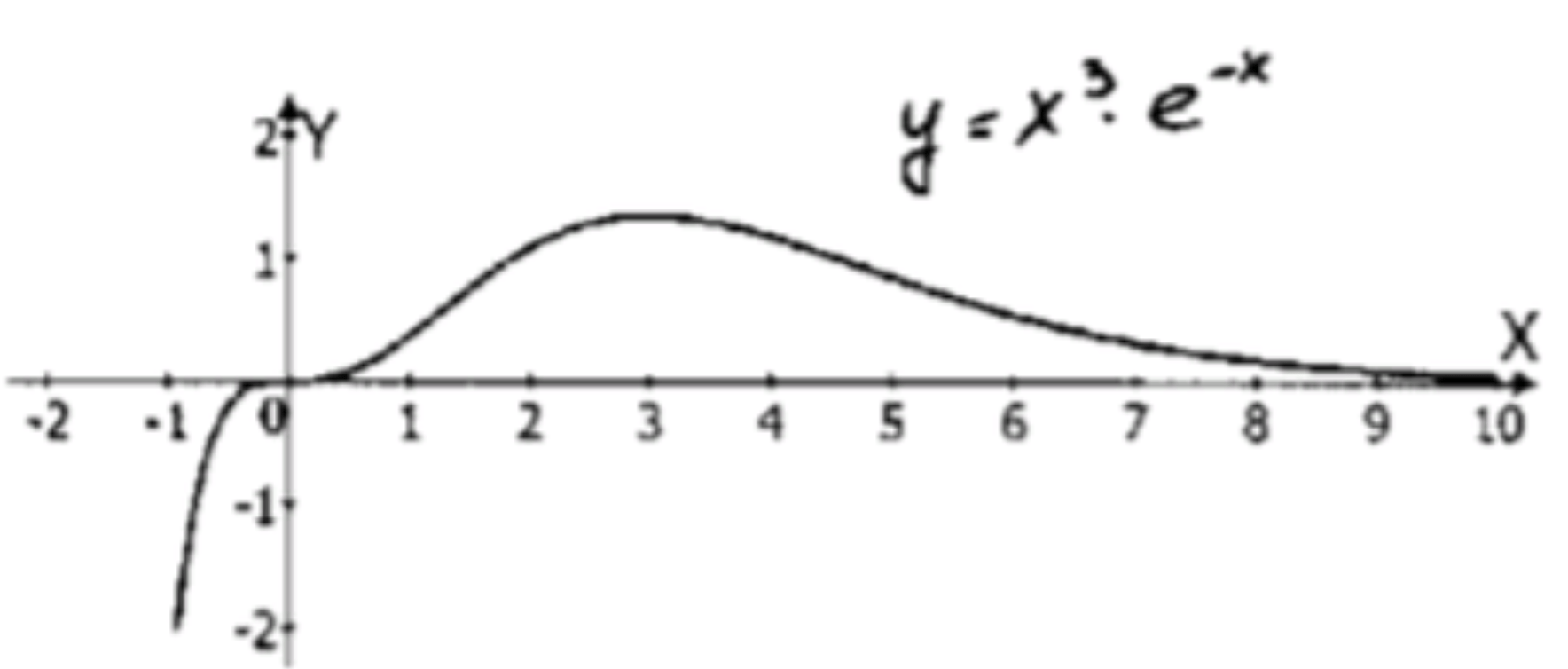
4) $y = x^3 \cdot e^{-x};$

а) Область определения:

$$D(x) = (-\infty; +\infty);$$

б) Производная функции:

$$y'(x) = (x^3)’ \cdot e^{-x} + x^3 \cdot (e^{-x})’;$$ $$y'(x) = 3x^2 \cdot e^{-x} — x^3 \cdot e^{-x};$$ $$y'(x) = e^{-x} \cdot (3x^2 — x^3).$$

в) Стационарные точки:

$$3x^2 — x^3 = 0;$$ $$x^2(3 — x) = 0;$$ $$x_1 = 0 \quad \text{и} \quad x_2 = 3;$$

г) Значения функции:

$$f(0) = 0^3 \cdot e^{0} = 0;$$ $$f(3) = 3^3 \cdot e^{-3} = \frac{27}{e^3}.$$

д) Уравнение горизонтальной асимптоты:

$$y=\underset{x\to \mathrm{\infty }}{\lim }{x}^3\cdot e^{-x}=0.$$

$$y = \lim_{x \to \infty} x^3 \cdot e^{-x} = 0.$$

Задача 1:

$y = (x^2 — 1) \cdot \sqrt{x + 1}$

а) Область определения функции $D(x)$:

Для того чтобы определить область определения функции, нужно учитывать:

1. Выражение $\sqrt{x + 1}$ определено, если $x + 1 \geq 0$, то есть $x \geq -1$.
2. Поскольку $x^2 — 1$ не имеет ограничений по области определения, область определения функции будет ограничена только условием $x + 1 \geq 0$.

Ответ: $D(x) = [-1; +\infty)$

б) Производная функции $y'(x)$:

Для нахождения производной функции, применим правило дифференцирования произведения двух функций, а также правило дифференцирования степени.

Функция представлена как произведение двух функций:

$$y(x) = (x^2 — 1) \cdot \sqrt{x + 1}$$

Чтобы найти производную, применяем формулу:

$$\frac{d}{dx} \left( f(x) \cdot g(x) \right) = f'(x) \cdot g(x) + f(x) \cdot g'(x)$$

Здесь:

• $f(x) = x^2 — 1$,
• $g(x) = \sqrt{x + 1} = (x + 1)^{1/2}$.

Дифференцируем $f(x) = x^2 — 1$:

$$f'(x) = 2x.$$

Дифференцируем $g(x) = (x + 1)^{1/2}$, используя правило дифференцирования степени:

$$g'(x) = \frac{1}{2} \cdot (x + 1)^{-1/2} = \frac{1}{2\sqrt{x + 1}}.$$

Теперь применим формулу для произведения:

$$y'(x) = (2x) \cdot \sqrt{x + 1} + (x^2 — 1) \cdot \frac{1}{2\sqrt{x + 1}}.$$

Приводим к общему знаменателю:

$$y'(x) = \frac{2x \cdot (x + 1) + (x^2 — 1)}{2\sqrt{x + 1}}.$$

Раскрываем скобки:

$$y'(x) = \frac{2x^2 + 2x + x^2 — 1}{2\sqrt{x + 1}} = \frac{3x^2 + 2x — 1}{2\sqrt{x + 1}}.$$

в) Стационарные точки:

Стационарные точки функции — это такие значения $x$, при которых производная функции равна нулю:

$$y'(x) = 0 \quad \Rightarrow \quad \frac{3x^2 + 2x — 1}{2\sqrt{x + 1}} = 0.$$

Для того чтобы дробь была равна нулю, числитель должен быть равен нулю:

$$3x^2 + 2x — 1 = 0.$$

Решаем это квадратное уравнение:

$$D = 2^2 — 4 \cdot 3 \cdot (-1) = 4 + 12 = 16,$$ $$x_1 = \frac{-2 — \sqrt{16}}{2 \cdot 3} = \frac{-2 — 4}{6} = \frac{-6}{6} = -1,$$ $$x_2 = \frac{-2 + \sqrt{16}}{2 \cdot 3} = \frac{-2 + 4}{6} = \frac{2}{6} = \frac{1}{3}.$$

Таким образом, стационарные точки: $x_1 = -1$ и $x_2 = \frac{1}{3}$.

г) Значения функции в стационарных точках:

Для $x = -1$:

$$f(-1) = ((-1)^2 — 1) \cdot \sqrt{-1 + 1} = (1 — 1) \cdot \sqrt{0} = 0.$$

Для $x = \frac{1}{3}$:

$$f\left( \frac{1}{3} \right) = \left( \left( \frac{1}{3} \right)^2 — 1 \right) \cdot \sqrt{\frac{1}{3} + 1} = \left( \frac{1}{9} — 1 \right) \cdot \sqrt{\frac{4}{3}} = \left( -\frac{8}{9} \right) \cdot \sqrt{\frac{4}{3}}.$$ $$f\left( \frac{1}{3} \right) = -\frac{8}{9} \cdot \frac{2}{\sqrt{3}} = -\frac{16}{9\sqrt{3}}.$$

д) Промежутки монотонности:

Для определения промежутков монотонности нужно исследовать знак производной на различных интервалах, используя стационарные точки.

• Производная функции $y'(x) = \frac{3x^2 + 2x — 1}{2\sqrt{x + 1}}$ будет изменяться в зависимости от знака числителя.
• Для $x \in (-\infty, -1)$, $y'(x) < 0$ (функция убывает).
• Для $x \in (-1, \frac{1}{3})$, $y'(x) > 0$ (функция возрастает).
• Для $x \in (\frac{1}{3}, +\infty)$, $y'(x) < 0$ (функция убывает).

Таким образом:

• Функция возрастает на интервале $(-1, \frac{1}{3})$,
• Функция убывает на интервалах $(-\infty, -1)$ и $(\frac{1}{3}, +\infty)$.

е) Таблица свойств функции:

$$\begin{array}{|c|c|c|c|} \hline x & -1 < x < \frac{1}{3} & x = \frac{1}{3} & \frac{1}{3} < x < +\infty \\ \hline f'(x) & + & 0 & — \\ \hline f(x) & \text{возрастает} & -\frac{16}{9\sqrt{3}} & \text{убывает} \\ \hline \end{array}$$

Задача 2:

$y = |x| \cdot \sqrt{1 + 3x}$

а) Область определения функции $D(x)$:

1. $|x|$ не имеет ограничений по области определения, так как абсолютное значение определено для всех $x$.
2. Для выражения $\sqrt{1 + 3x}$, подкоренное выражение должно быть неотрицательным, то есть:

$$1 + 3x \geq 0 \quad \Rightarrow \quad x \geq -\frac{1}{3}.$$

Ответ: $D(x) = \left[-\frac{1}{3}; +\infty\right)$.

б) Производная функции $y'(x)$:

Функция состоит из произведения двух частей:

$$y(x) = |x| \cdot \sqrt{1 + 3x}.$$

Для вычисления производной будем учитывать, что производная модуля зависит от знака $x$.

Разделим рассмотрение на два случая:

1. Когда $x \geq 0$:

$$|x| = x, \quad y(x) = x \cdot \sqrt{1 + 3x}.$$

Применим правило дифференцирования произведения:

$$y'(x) = (x)’ \cdot \sqrt{1 + 3x} + x \cdot (\sqrt{1 + 3x})’.$$

Дифференцируем каждую часть:

• $(x)’ = 1$,
• $(\sqrt{1 + 3x})’ = \frac{1}{2} \cdot (1 + 3x)^{-1/2} \cdot 3 = \frac{3}{2\sqrt{1 + 3x}}$.

Получаем:

$$y'(x) = \sqrt{1 + 3x} + x \cdot \frac{3}{2\sqrt{1 + 3x}}.$$

2. Когда $x < 0$:

$$|x| = -x, \quad y(x) = -x \cdot \sqrt{1 + 3x}.$$

Применяем ту же самую формулу для производной:

$$y'(x) = (-x)’ \cdot \sqrt{1 + 3x} + (-x) \cdot (\sqrt{1 + 3x})’.$$

• $(-x)’ = -1$,
• $(\sqrt{1 + 3x})’ = \frac{3}{2\sqrt{1 + 3x}}$.

Получаем:

$$y'(x) = -\sqrt{1 + 3x} — x \cdot \frac{3}{2\sqrt{1 + 3x}}.$$

Таким образом, производная функции будет:

$$y'(x) = \pm \left( \sqrt{1 + 3x} + x \cdot \frac{3}{2\sqrt{1 + 3x}} \right), \quad \text{для} \quad x \geq 0 \quad \text{и} \quad x < 0.$$

в) Стационарные точки:

Для нахождения стационарных точек, приравняем производную к нулю.

Для $x \geq 0$:

$$y'(x) = \sqrt{1 + 3x} + x \cdot \frac{3}{2\sqrt{1 + 3x}} = 0.$$

Умножим обе части на $2\sqrt{1 + 3x}$ для избавления от дроби:

$$2(1 + 3x) + 3x = 0.$$

Раскрываем скобки:

$$2 + 6x + 3x = 0 \quad \Rightarrow \quad 2 + 9x = 0 \quad \Rightarrow \quad x = -\frac{2}{9}.$$

Так как $x \geq 0$, это значение не подходит для этого случая.

Для $x < 0$:

$$y'(x) = -\sqrt{1 + 3x} — x \cdot \frac{3}{2\sqrt{1 + 3x}} = 0.$$

Аналогично, умножим на $2\sqrt{1 + 3x}$:

$$-2(1 + 3x) — 3x = 0.$$

Раскрываем скобки:

$$-2 — 6x — 3x = 0 \quad \Rightarrow \quad -2 — 9x = 0 \quad \Rightarrow \quad x = -\frac{2}{9}.$$

Так как $x < 0$, это значение подходит. Таким образом, стационарная точка — это $x = -\frac{2}{9}$.

г) Значение функции в стационарной точке:

Найдем значение функции в точке $x = -\frac{2}{9}$:

$$f\left( -\frac{2}{9} \right) = \left| -\frac{2}{9} \right| \cdot \sqrt{1 + 3 \cdot \left( -\frac{2}{9} \right)} = \frac{2}{9} \cdot \sqrt{1 — \frac{6}{9}} = \frac{2}{9} \cdot \sqrt{\frac{3}{9}} = \frac{2}{9} \cdot \frac{\sqrt{3}}{3}.$$ $$f\left( -\frac{2}{9} \right) = \frac{2 \sqrt{3}}{27}.$$

д) Промежутки монотонности:

Для анализа промежутков монотонности нужно исследовать знак производной:

1. Для $x \geq 0$, $y'(x)$ всегда положительно, так как обе составляющие ($\sqrt{1 + 3x}$ и $\frac{3x}{2\sqrt{1 + 3x}}$) положительны.
2. Для $x < 0$, $y'(x)$ отрицательно, так как обе составляющие ($-\sqrt{1 + 3x}$ и $-\frac{3x}{2\sqrt{1 + 3x}}$) отрицательны.

Следовательно:

• Функция возрастает на $\left[ -\frac{2}{9}; +\infty \right)$,
• Функция убывает на $\left[ -\infty; -\frac{2}{9} \right)$.

е) Таблица свойств функции:

$$\begin{array}{|c|c|c|c|c|} \hline x & x < -\frac{2}{9} & x = -\frac{2}{9} & -\frac{2}{9} < x < 0 & x > 0 \\ \hline f'(x) & — & 0 & + & + \\ \hline f(x) & \text{убывает} & \frac{2\sqrt{3}}{27} & \text{возрастает} & \text{возрастает} \\ \hline \end{array}$$

Задача 3:

$y = x^2 \cdot e^{-x}$

а) Область определения:

Для функции $y = x^2 \cdot e^{-x}$ нет ограничений по области определения, так как и $x^2$, и $e^{-x}$ определены для всех значений $x$.

Ответ: $D(x) = (-\infty; +\infty)$.

б) Производная функции:

Используем правило произведения для нахождения производной функции:

$$y'(x) = (x^2)’ \cdot e^{-x} + x^2 \cdot (e^{-x})’.$$

Дифференцируем:

$$(x^2)’ = 2x, \quad (e^{-x})’ = -e^{-x}.$$

Получаем:

$$y'(x) = 2x \cdot e^{-x} — x^2 \cdot e^{-x} = e^{-x} \cdot (2x — x^2).$$

в) Стационарные точки:

Стационарные точки находим из уравнения $y'(x) = 0$:

$$e^{-x} \cdot (2x — x^2) = 0.$$

Поскольку $e^{-x} \neq 0$ для всех $x$, остаётся:

$$2x — x^2 = 0 \quad \Rightarrow \quad x(2 — x) = 0.$$

Таким образом, $x_1 = 0$ и $x_2 = 2$.

г) Значения функции:

Для $x = 0$:

$$f(0) = 0^2 \cdot e^{0} = 0.$$

Для $x = 2$:

$$f(2) = 2^2 \cdot e^{-2} = \frac{4}{e^2}.$$

д) Уравнение горизонтальной асимптоты:

Для нахождения горизонтальной асимптоты анализируем поведение функции при $x \to \infty$:

$$\lim_{x \to \infty} x^2 \cdot e^{-x} = 0.$$

е) Промежутки монотонности:

Производная функции:

$$y'(x) = e^{-x} \cdot (2x — x^2).$$

• Функция возрастает на интервале $(0; 2)$,
• Функция убывает на интервале $(2; +\infty)$.

Таблица свойств функции:

$$\begin{array}{|c|c|c|c|c|} \hline x & x < 0 & 0 & 0 < x < 2 & x > 2 \\ \hline f'(x) & — & 0 & + & — \\ \hline f(x) & \text{убывает} & 0 & \text{возрастает} & \text{убывает} \\ \hline \end{array}$$

Задача 4:

$y = x^3 \cdot e^{-x}$

а) Область определения:

Для функции $y = x^3 \cdot e^{-x}$ нет ограничений по области определения, так как и $x^3$, и $e^{-x}$ определены для всех значений $x$.

Ответ: $D(x) = (-\infty; +\infty)$.

б) Производная функции:

Используем правило произведения для нахождения производной функции:

$$y'(x) = (x^3)’ \cdot e^{-x} + x^3 \cdot (e^{-x})’.$$

Дифференцируем:

$$(x^3)’ = 3x^2, \quad (e^{-x})’ = -e^{-x}.$$

Получаем:

$$y'(x) = 3x^2 \cdot e^{-x} — x^3 \cdot e^{-x} = e^{-x} \cdot (3x^2 — x^3).$$

в) Стационарные точки:

Стационарные точки находим из уравнения $y'(x) = 0$:

$$e^{-x} \cdot (3x^2 — x^3) = 0.$$

Поскольку $e^{-x} \neq 0$ для всех $x$, остается:

$$3x^2 — x^3 = 0.$$

Вынесем общий множитель $x^2$:

$$x^2(3 — x) = 0.$$

Таким образом, $x_1 = 0$ и $x_2 = 3$.

г) Значения функции:

Для $x = 0$:

$$f(0) = 0^3 \cdot e^0 = 0.$$

Для $x = 3$:

$$f(3) = 3^3 \cdot e^{-3} = \frac{27}{e^3}.$$

д) Уравнение горизонтальной асимптоты:

Для нахождения горизонтальной асимптоты анализируем поведение функции при $x \to \infty$:

$$\lim_{x \to \infty} x^3 \cdot e^{-x} = 0.$$

е) Промежутки монотонности:

Производная функции:

$$y'(x) = e^{-x} \cdot (3x^2 — x^3).$$

1. Для $x = 0$, $y'(0) = 0$, точка минимума.
2. Для $x > 0$, знак производной зависит от выражения $3x^2 — x^3$:
   • Когда $0 < x < 3$, $3x^2 — x^3 > 0$ (функция возрастает).
   • Когда $x > 3$, $3x^2 — x^3 < 0$ (функция убывает).

Таким образом, функция возрастает на интервале $(0; 3)$ и убывает на интервале $(3; +\infty)$.

Таблица свойств функции:

$$\begin{array}{|c|c|c|c|c|} \hline x & x < 0 & x = 0 & 0 < x < 3 & x > 3 \\ \hline f'(x) & — & 0 & + & — \\ \hline f(x) & \text{убывает} & 0 & \text{возрастает} & \text{убывает} \\ \hline \end{array}$$