ГДЗ по Алгебре 10-11 Класс Номер 976 Алимов — Подробные Ответы

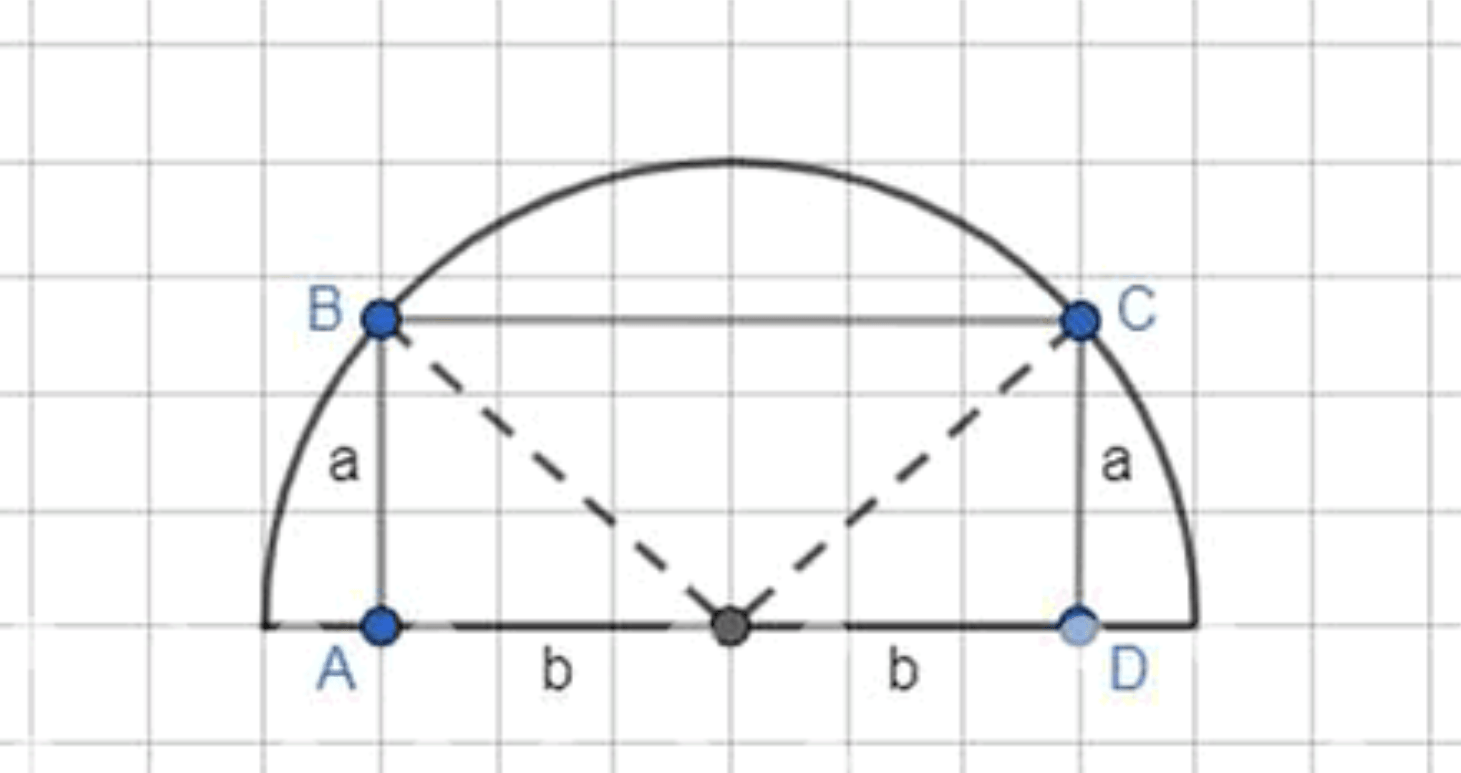
Из всех прямоугольников, вписанных в полукруг радиуса R так, что одна сторона прямоугольника лежит на диаметре полукруга, выбран тот, у которого наибольшая площадь. Найти эту площадь.

Отобразим условие задачи:

Пусть $a$ и $b$ — длины сторон прямоугольника, тогда:

$$b = 2 \cdot \sqrt{R^2 — a^2};$$ $$S(a) = a \cdot b = 2a \cdot \sqrt{R^2 — a^2};$$

Производная функции:

$$S'(a) = (2a)’ \cdot \sqrt{R^2 — a^2} + 2a \cdot (R^2 — a^2)^{\frac{1}{2}};$$ $$S'(a) = 2 \cdot \sqrt{R^2 — a^2} + 2a \cdot \frac{1}{2} \cdot (-2a) \cdot (R^2 — a^2)^{-\frac{1}{2}};$$ $$S'(a) = 2 \sqrt{R^2 — a^2} — \frac{2a^2}{\sqrt{R^2 — a^2}};$$ $$S'(a) = 2 \cdot \frac{R^2 — a^2 — a^2}{\sqrt{R^2 — a^2}};$$ $$S'(a) = 2 \cdot \frac{R^2 — 2a^2}{\sqrt{R^2 — a^2}};$$

Промежуток возрастания:

$$R^2 — 2a^2 > 0;$$ $$2a^2 < R^2;$$ $$a^2 < \frac{R^2}{2};$$ $$-\frac{R}{\sqrt{2}} < a < \frac{R}{\sqrt{2}};$$

Искомые значения:

$$a = \frac{R}{\sqrt{2}} \quad \text{— точка максимума};$$ $$S\left(\frac{R}{\sqrt{2}}\right) = 2 \cdot \frac{R}{\sqrt{2}} \cdot \sqrt{R^2 — \frac{R^2}{2}} = 2R \cdot \sqrt{\frac{R^2}{2}} = \frac{2R}{\sqrt{2}} \cdot \frac{R}{\sqrt{2}} = R^2;$$

Ответ:

$$\boxed{R^2}$$

1. Построение и обозначения

Рассмотрим полукруг с радиусом $R$. Пусть прямоугольник вписан в этот полукруг таким образом, что одна его сторона лежит на диаметре. Пусть:

• $a$ — длина вертикальной стороны прямоугольника,
• $b$ — длина горизонтальной стороны прямоугольника.

Из условия задачи, так как прямоугольник вписан в полукруг, его верхние углы лежат на окружности, и поэтому для каждого прямоугольника выполняется следующая геометрическая зависимость:

$$a^2 + b^2 = R^2.$$

Далее, из условия задачи нам нужно найти максимальную площадь прямоугольника.

2. Площадь прямоугольника

Площадь прямоугольника $S$ равна:

$$S = a \cdot b.$$

Но из геометрического условия $b = 2 \sqrt{R^2 — a^2}$, следовательно:

$$S(a) = a \cdot b = a \cdot 2 \sqrt{R^2 — a^2} = 2a \sqrt{R^2 — a^2}.$$

Это функция площади в зависимости от $a$.

3. Поиск максимума площади

Чтобы найти максимальную площадь, нужно найти производную функции $S(a)$. Для этого воспользуемся правилом произведения и цепным правилом:

$$S'(a) = 2 \left( \sqrt{R^2 — a^2} + a \cdot \frac{d}{da} \left( \sqrt{R^2 — a^2} \right) \right).$$

Производная $\frac{d}{da} \left( \sqrt{R^2 — a^2} \right)$ будет:

$$\frac{d}{da} \left( \sqrt{R^2 — a^2} \right) = \frac{-2a}{2\sqrt{R^2 — a^2}} = \frac{-a}{\sqrt{R^2 — a^2}}.$$

Теперь подставим это в выражение для $S'(a)$:

$$S'(a) = 2 \left( \sqrt{R^2 — a^2} — \frac{a^2}{\sqrt{R^2 — a^2}} \right).$$

Приведем к общему знаменателю:

$$S'(a) = 2 \cdot \frac{R^2 — 2a^2}{\sqrt{R^2 — a^2}}.$$

4. Нахождение критических точек

Для нахождения максимума приравняем производную к нулю:

$$S'(a) = 0 \quad \Rightarrow \quad R^2 — 2a^2 = 0 \quad \Rightarrow \quad a^2 = \frac{R^2}{2} \quad \Rightarrow \quad a = \frac{R}{\sqrt{2}}.$$

5. Максимальная площадь

Теперь, подставим найденное значение $a = \frac{R}{\sqrt{2}}$ в выражение для площади $S(a)$:

$$S\left( \frac{R}{\sqrt{2}} \right) = 2 \cdot \frac{R}{\sqrt{2}} \cdot \sqrt{R^2 — \left( \frac{R}{\sqrt{2}} \right)^2} = 2 \cdot \frac{R}{\sqrt{2}} \cdot \sqrt{\frac{R^2}{2}} = 2 \cdot \frac{R}{\sqrt{2}} \cdot \frac{R}{\sqrt{2}} = R^2.$$

6. Ответ

Максимальная площадь прямоугольника, вписанного в полукруг радиуса $R$, равна $R^2$.

Ответ: $R^2$.