ГДЗ по Алгебре 10-11 Класс Номер 949 Алимов — Подробные Ответы

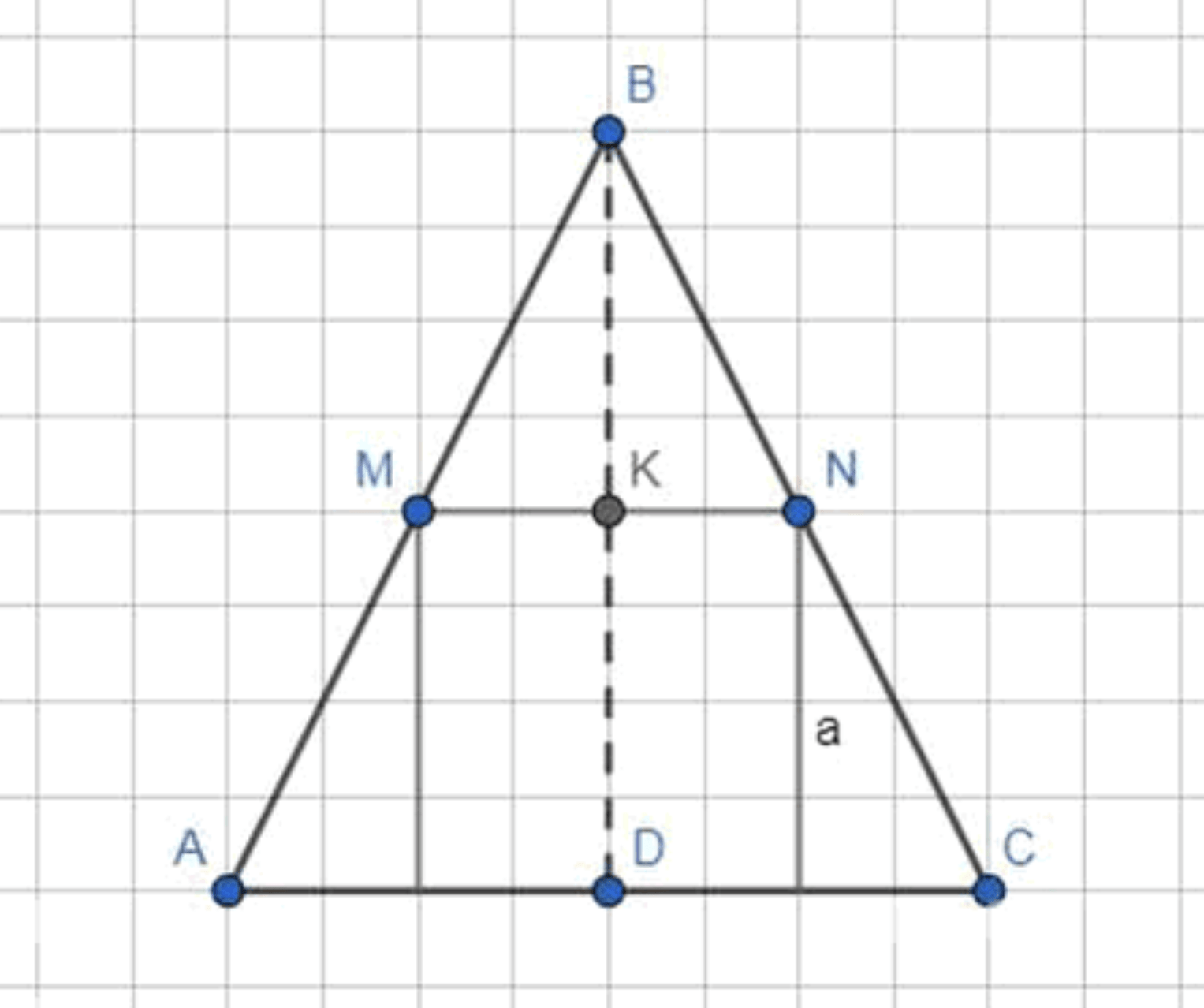
Равнобедренные треугольники описаны около квадрата со стороной а так, что одна сторона квадрата лежит на основании треугольника (рис. 142). Обозначая ВК = х, найти такое значение х, при котором площадь треугольника наименьшая.

Отобразим условие задачи:

Отрезок $KD$ равен стороне квадрата, то есть $KD=a$, значит:
$BD=BK+KD=x+a;$

Рассмотрим параллельные прямые $MN$ и $AC$ и секущую $AB$:
$\mathrm{\angle }BMN=\mathrm{\angle }BAC(\text{как соответственные углы});$

Треугольники $ABC$ и $BMN$ подобны ($\mathrm{\angle }BMN=\mathrm{\angle }BAC$ и $\mathrm{\angle }B$ — общий):
$\frac{AC}{MN}=\frac{BD}{BK}=\frac{x+a}{x};$
$AC=\frac{(x+a)\cdot MN}{x}=\frac{(x+a)\cdot a}{x}=\frac{ax+a^2}{x}=a+\frac{a^2}{x};$

Площадь треугольника:

$S(x)=\frac{1}{2}\cdot AC\cdot BD=\frac{1}{2}\cdot (a+\frac{a^2}{x})\cdot (x+a);$
$S(x)=\frac{1}{2}\cdot (ax+a^2+\frac{a^3}{x}+a^2);$
$S(x)=\frac{1}{2}\cdot (2a^2+ax+\frac{a^3}{x});$
$S(x)=a^2+\frac{ax}{2}+\frac{a^3}{2x};$

Производная функции:

$S^{\mathrm{\prime }}(x)={\left(a^2\right)}^{\mathrm{\prime }}+\frac{a}{2}\cdot (x{)}^{\mathrm{\prime }}+\frac{a^3}{2}\cdot {\left(\frac{1}{x}\right)}^{\mathrm{\prime }};$
$S^{\mathrm{\prime }}(x)=0+\frac{a}{2}-\frac{a^3}{2x^2}=\frac{a}{2}\cdot (1-\frac{a^2}{x^2});$

Промежуток возрастания:

$1-\frac{a^2}{x^2}>0;$
$x^2-a^2>0;$
$x^2>a^2;$
$x<-a\text{или}x>a;$

Искомое значение:

$x=a\text{— точка минимума};$

Ответ:

$BK=a\mathrm{.}$

1. Анализ условия

Пусть у нас есть квадрат со стороной $a$, и точка $K$ расположена на одной из сторон квадрата. От этой точки проводится отрезок $KD$, который равен стороне квадрата, то есть:

$$KD=a$$

Рассмотрим отрезок $BD$, который состоит из двух частей:

• $BK=x$ — переменная величина, расстояние от точки $B$ до точки $K$,
• $KD=a$ — фиксированная длина, как сказано выше.

Следовательно:

$$BD=BK+KD=x+a$$

2. Подобие треугольников

Даны две параллельные прямые:

• $MN\parallel AC$
• и секущая прямая $AB$, пересекающая обе параллельные прямые.

По правилу о соответственных углах, если секущая пересекает две параллельные прямые, то соответствующие углы равны:

$$\mathrm{\angle }BMN=\mathrm{\angle }BAC$$

Также известно, что у треугольников $ABC$ и $BMN$ есть общий угол $\mathrm{\angle }B$. Таким образом, по двум углам можно утверждать, что треугольники подобны:

$$\mathrm{△}ABC\sim \mathrm{△}BMN$$

3. Пропорциональность сторон подобных треугольников

Из подобия треугольников следует пропорция между соответствующими сторонами:

$$\frac{AC}{MN}=\frac{BD}{BK}$$

Подставим известные величины:

• $MN=a$ (сторона квадрата),
• $BD=x+a$,
• $BK=x$

$$\frac{AC}{a}=\frac{x+a}{x}$$

Отсюда выразим длину $AC$:

$$AC=\frac{(x+a)\cdot a}{x}=\frac{a(x+a)}{x}$$

Раскроем скобки:

$$AC=\frac{ax+a^2}{x}=a+\frac{a^2}{x}$$

4. Формула площади треугольника

Теперь найдём площадь треугольника $\mathrm{△}ABC$. По формуле площади треугольника:

$$S=\frac{1}{2}\cdot \text{основание}\cdot \text{высоту}$$

Пусть основание — $AC$, а высота, опущенная из точки $B$, — $BD$.

$$S(x)=\frac{1}{2}\cdot AC\cdot BD$$

Подставим найденные ранее выражения:

• $AC=a+\frac{a^2}{x}$
• $BD=x+a$

$$S(x)=\frac{1}{2}\cdot (a+\frac{a^2}{x})\cdot (x+a)$$

Раскроем скобки:

$$S(x)=\frac{1}{2}\cdot (ax+a^2+\frac{a^3}{x}+a^2)$$

Объединим подобные слагаемые:

$$S(x)=\frac{1}{2}\cdot (ax+2a^2+\frac{a^3}{x})$$

Разделим каждое слагаемое на 2:

$$S(x)=a^2+\frac{ax}{2}+\frac{a^3}{2x}$$

5. Нахождение производной

Для нахождения экстремума (максимума или минимума площади), найдём производную $S^{\mathrm{\prime }}(x)$:

$$S(x)=a^2+\frac{ax}{2}+\frac{a^3}{2x}$$

Производная суммы равна сумме производных:

• $(a^2{)}^{\mathrm{\prime }}=0$, так как это константа,
• ${\left(\frac{ax}{2}\right)}^{\mathrm{\prime }}=\frac{a}{2}$,
• ${\left(\frac{a^3}{2x}\right)}^{\mathrm{\prime }}=-\frac{a^3}{2x^2}$, используя производную от $\frac{1}{x}$

Итак:

$$S^{\mathrm{\prime }}(x)=\frac{a}{2}-\frac{a^3}{2x^2}$$

Вынесем общий множитель $\frac{a}{2}$:

$$S^{\mathrm{\prime }}(x)=\frac{a}{2}(1-\frac{a^2}{x^2})$$

6. Исследование производной на знак (возрастание/убывание)

Найдём, когда функция возрастает, т.е. когда $S^{\mathrm{\prime }}(x)>0$:

$$\frac{a}{2}(1-\frac{a^2}{x^2})>0$$

Поскольку $a>0$, знак производной определяется знаком выражения в скобках:

$$1-\frac{a^2}{x^2}>0\Rightarrow \frac{a^2}{x^2}<1$$

Домножим обе части на $x^2$ (учитываем, что $x\mathrm{\ne }0$):

$$a^2<x^2\Rightarrow x^2>a^2$$

Извлекая корень (учитывая знак x):

$$x<-a\text{или}x>a$$

Значит, на этих промежутках функция возрастает.

7. Определение точки минимума

Так как функция возрастает при $x<-a$ и $x>a$, а между ними убывает, то точка минимума — это граничное значение:

$$x=a$$

Подставим это значение, чтобы найти точку минимума.

8. Ответ

$$BK=a$$