
Учебник «Алгебра» для 10-11 классов под авторством Алимова – это один из наиболее популярных и широко используемых учебных пособий для старшеклассников. Он заслужил признание как среди учителей, так и среди учеников благодаря своей структурированности, доступности изложения и качественной проработке материала.
ГДЗ по Алгебре 10-11 Класс Номер 933 Алимов — Подробные Ответы
1)
а) Область определения:
б) Производная функции:
в) Стационарные точки:
г) Значения функции:
д) Промежутки монотонности:
- Возрастает на и
- Убывает на и
- — точка минимума
- — точка максимума
е) Таблица свойств функции:
2)
а) Область определения:
б) Производная функции:
в) Стационарные точки:
г) Значения функции:
д) Промежутки монотонности:
- Возрастает на и
- Убывает на и
- — точка минимума
- — точка максимума
е) Таблица свойств функции:
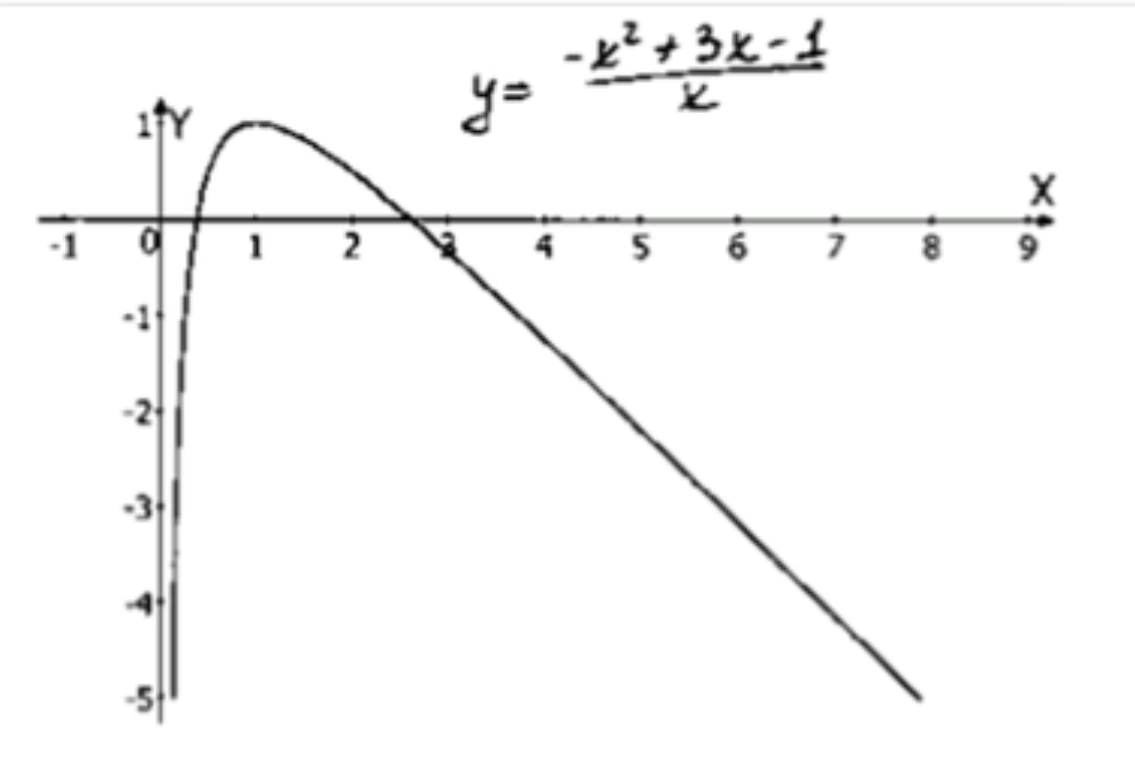
1)
а) Область определения:
Область определения функции зависит от выражения . Функция не определена при , так как при знаменатель становится равным нулю. Следовательно, область определения функции:
Ответ:
б) Производная функции:
Для нахождения производной функции , используем правило дифференцирования дроби (правило частного):
Здесь:
- Производная от равна ,
- Производная от равна 1.
Подставим эти значения в формулу:
Теперь упростим числитель:
Раскроем скобки в числителе:
Ответ:
в) Стационарные точки:
Стационарные точки функции находятся, когда производная равна нулю:
Для того чтобы дробь равнялась нулю, числитель должен быть равен нулю (поскольку знаменатель всегда положителен):
Решаем это уравнение:
Таким образом, и .
Ответ:
Стационарные точки: ,
г) Значения функции:
Теперь подставим найденные стационарные точки и в исходную функцию .
Для :
Для :
Ответ:
д) Промежутки монотонности:
Для анализа промежутков монотонности, изучим знак производной .
- В числителе: , который меняет знак в точках и .
- Знаменатель всегда положителен, поэтому знак производной определяется знаком числителя.
Для (например, ):
Это означает, что функция возрастает на интервале .
Для (например, ):
Это отрицательное значение говорит о том, что функция убывает на интервале .
Для (например, ):
Это также отрицательное значение говорит о том, что функция убывает на интервале .
Для (например, ):
Это положительное значение говорит о том, что функция возрастает на интервале .
Ответ:
- Возрастает на и
- Убывает на и
- — точка минимума
- — точка максимума
е) Таблица свойств функции:
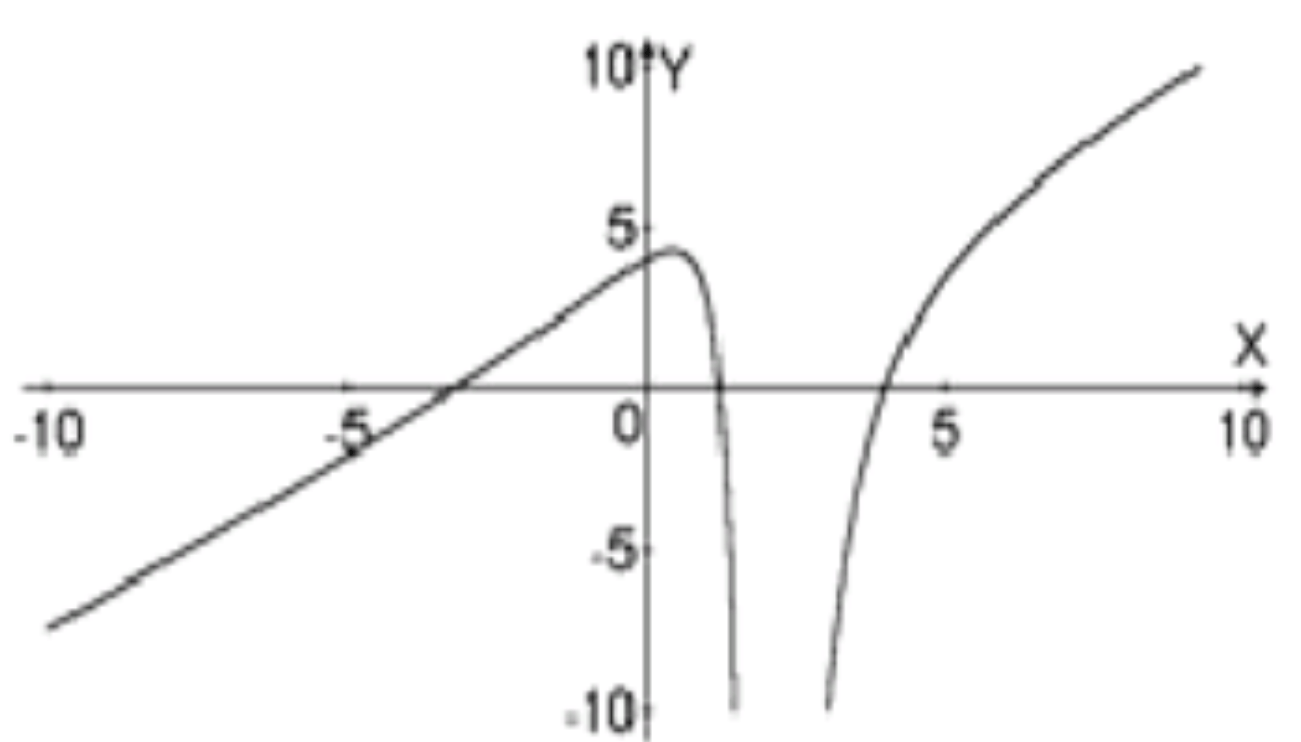
2)
а) Область определения:
Функция содержит выражение , которое не определено при . Следовательно, область определения функции:
Ответ:
б) Производная функции:
Для нахождения производной функции применяем правила дифференцирования:
- Производная от равна ,
- Производная от равна 0,
- Производная от равна .
Таким образом, производная функции:
Ответ:
в) Стационарные точки:
Стационарные точки находятся, когда производная равна нулю:
Решаем это уравнение:
Ответ:
Стационарные точки: ,
г) Значения функции:
Теперь подставим стационарные точки и в исходную функцию .
Для :
Для :
Ответ:
д) Промежутки монотонности:
Для (например, ):
Функция убывает на .
Для (например, ):
Функция возрастает на .
Для (например, ):
Функция возрастает на .
Для (например, ):
Функция убывает на .
Ответ:
- Возрастает на и
- Убывает на и
- — точка минимума
- — точка максимума
е) Таблица свойств функции:
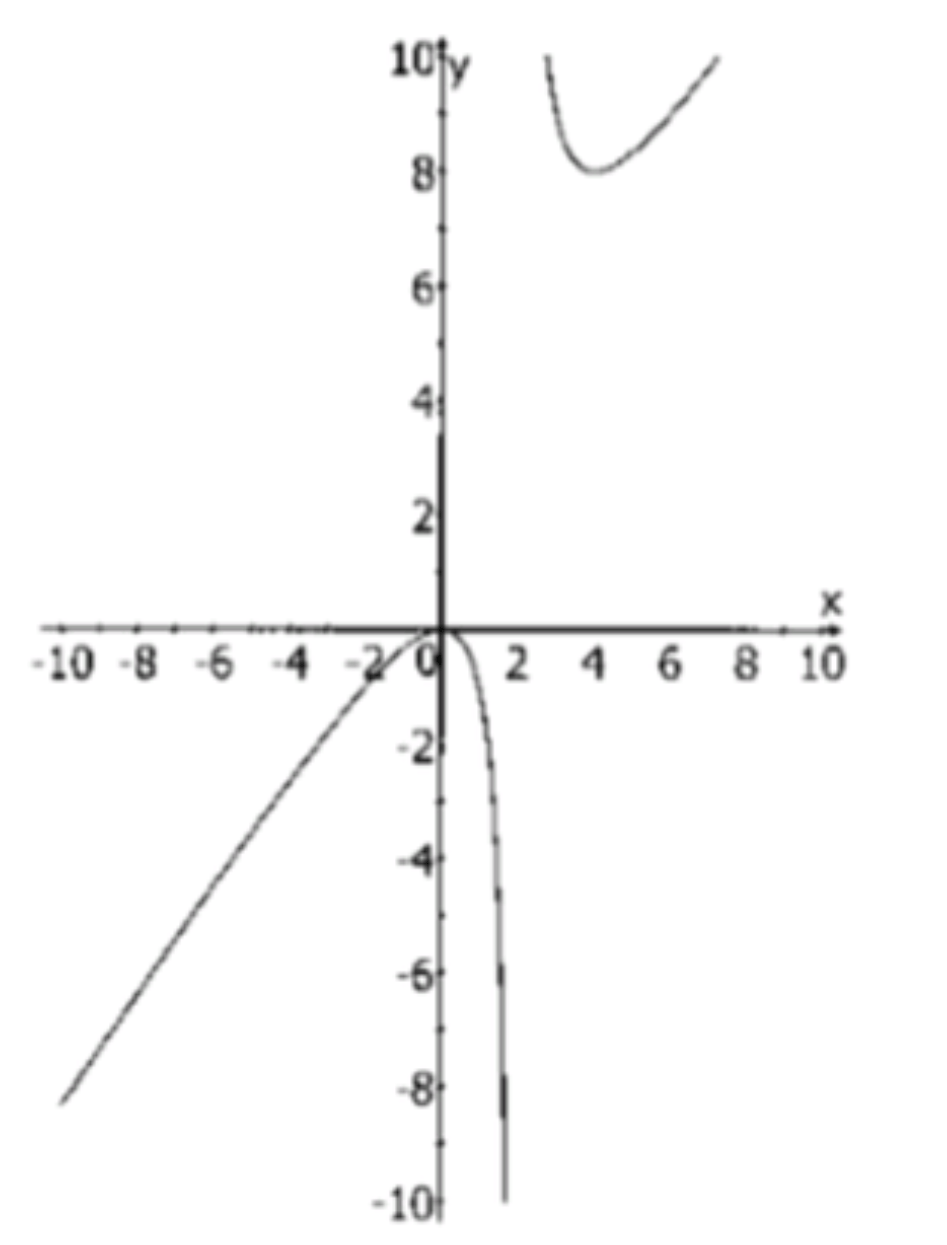
3)
а) Область определения:
Функция имеет выражение в знаменателе. Эта функция не определена при , так как знаменатель будет равен нулю. Следовательно, область определения:
Ответ:
б) Производная функции:
Для нахождения производной функции , используем правило дифференцирования дроби:
Рассчитаем производные в числителе:
- Производная от равна ,
- Производная от равна .
Подставим эти значения:
Продолжаем упрощать, раскрывая скобки и получаем:
Ответ:
в) Стационарные точки:
Стационарные точки находятся, когда производная равна нулю:
Находим дискриминант:
Решаем квадратное уравнение:
Таким образом, является точкой, в которой функция не определена, а — это точка стационарная.
Ответ:
Стационарная точка:
г) Значения функции:
Для нахождения значений функции в точках стационарности подставим в исходную функцию:
После упрощения:
Ответ:
Значение функции в стационарной точке:
д) Промежутки монотонности:
Для определения промежутков монотонности рассмотрим знак производной. Мы знаем, что функция возрастает, если производная положительна, и убывает, если производная отрицательна. Мы можем использовать знаки выражения , чтобы определить промежутки возрастания и убывания.
Ответ:
- Возрастает на и
- Убывает на
- — точка максимума
е) Таблица свойств функции:



Оставь свой отзыв 💬
Комментариев пока нет, будьте первым!