
Учебник «Алгебра» для 10-11 классов под авторством Алимова – это один из наиболее популярных и широко используемых учебных пособий для старшеклассников. Он заслужил признание как среди учителей, так и среди учеников благодаря своей структурированности, доступности изложения и качественной проработке материала.
ГДЗ по Алгебре 10-11 Класс Номер 925 Алимов — Подробные Ответы
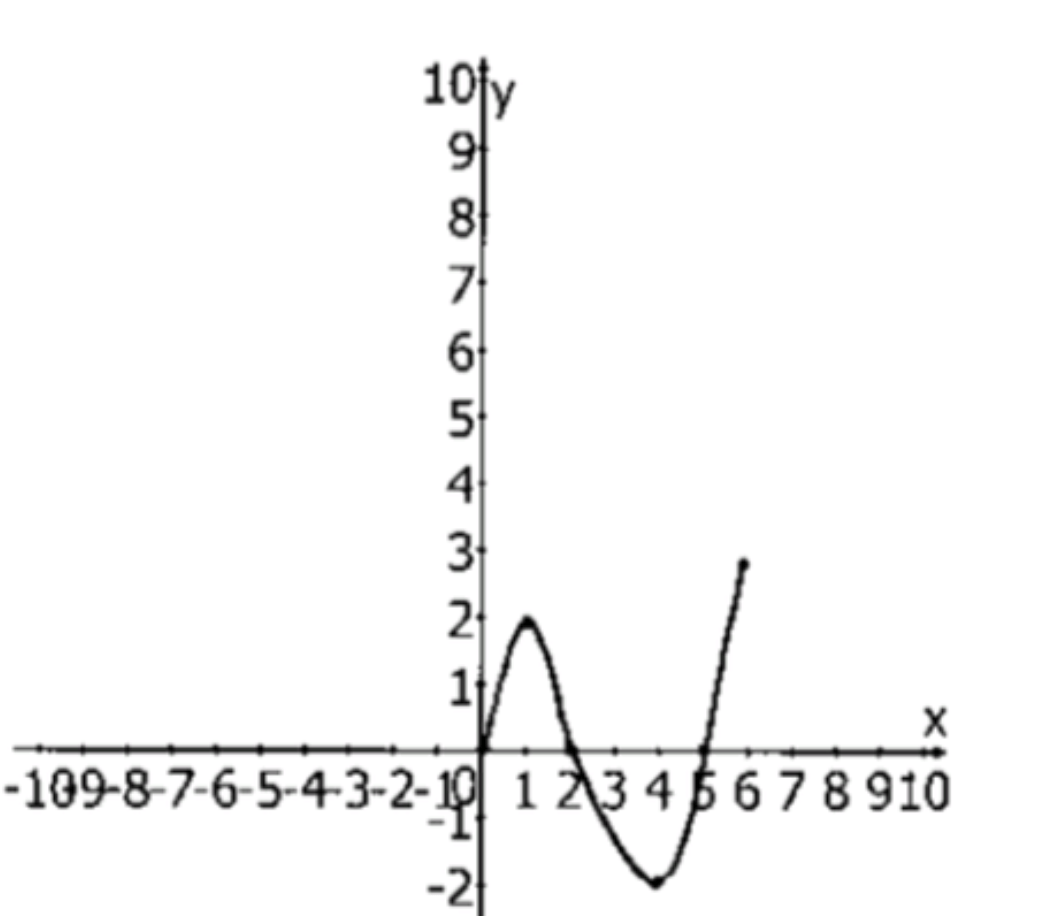
На отрезке [0; 6] изобразить эскиз графика непрерывной функции у = f(х), пользуясь данными, приведёнными в таблице. Учесть, что f (2) = 0, f (5) = 0.
Эскиз графика непрерывной функции, определенной на отрезке :
| 0 | 1 | 4 | 6 | ||||
|---|---|---|---|---|---|---|---|
| + | 0 | – | 0 | + | |||
| 0 | ↑ | 2 | ↓ | –2 | ↑ | 3 |
А также , ;
Нам нужно проанализировать график функции , которая определена на отрезке , и которая обладает следующим поведением:
- График функции представлен таблицей, в которой указаны производные функции и значения самой функции на разных интервалах.
- Также даны точки, в которых функция принимает конкретные значения: и .
Структура таблицы:
| 0 | 1 | 4 | 6 | ||||
|---|---|---|---|---|---|---|---|
| + | 0 | – | 0 | + | |||
| 0 | ↑ | 2 | ↓ | –2 | ↑ | 3 |
Анализ таблицы:
1. Интервал :
- На этом интервале: . Это значит, что производная функции положительна, а следовательно, сама функция на этом участке возрастает.
- Значение , а функция возрастает, значит график будет подниматься вверх.
- На интервале функция монотонно увеличивается.
2. Точка :
- В точке значение производной , что говорит о том, что функция на этой точке достигает локального экстремума.
- Кроме того, нам дается, что . Это указывает на то, что в точке график функции достигает максимума на данном интервале (так как на интервале функция возрастала).
3. Интервал :
- На этом интервале: . Это означает, что производная функции отрицательна, и следовательно, сама функция на данном интервале убывает.
- Значение при , и функция начинает убывать. Таким образом, график будет опускаться.
- Точка является особой, так как нам дано, что . Это означает, что на интервале функция проходит через точку .
4. Точка :
- В точке снова , что говорит о том, что функция снова достигает экстремума.
- Кроме того, , что означает, что функция принимает минимальное значение на интервале . Это будет точка локального минимума.
5. Интервал :
- На этом интервале: , что означает, что производная функции положительна, а следовательно, функция на этом интервале возрастает.
- Значение , и функция начинает увеличиваться, поднимаясь вверх.
- Точка сообщает, что функция пересекает ось абсцисс в точке . Таким образом, на интервале функция снова возрастает.
6. Точка :
- В точке мы видим, что функция достигает значения .
- Производная в точке отсутствует в таблице, но поскольку на интервале функция возрастала, можно предположить, что функция продолжает увеличиваться.
Подробное описание графика:
Начало графика:
- На интервале от до функция начинает с и возрастает.
- К точке функция достигает максимума и принимает значение .
Понижение на интервале :
- На интервале функция начинает убывать, проходя через точку , где , и достигает минимума в точке , где .
Повышение на интервале :
- После точки функция начинает снова возрастать. На интервале она поднимется, проходя через точку , и достигнет значения .
Выводы:
- Функция на отрезке состоит из трёх фаз: возрастания на интервале , убывания на интервале , и снова возрастания на интервале .
- Важные точки: , , , , , .
- Производная меняет знак на разных интервалах, что указывает на экстремумы функции в точках и , а также на изменение направления возрастания и убывания функции.



Оставь свой отзыв 💬
Комментариев пока нет, будьте первым!