ГДЗ по Алгебре 10-11 Класс Учебник 📕 Алимов — Все Части

Алгебра

10-11 класс учебник Алимов

10 класс

Тип

ГДЗ, Решебник.

Автор

Ш.А. Алимов, Ю.М. Колягин, М.В. Ткачева.

Год

2015-2024.

Издательство

Просвещение.

Описание

Учебник «Алгебра» для 10-11 классов под авторством Алимова – это один из наиболее популярных и широко используемых учебных пособий для старшеклассников. Он заслужил признание как среди учителей, так и среди учеников благодаря своей структурированности, доступности изложения и качественной проработке материала.

Учебник охватывает весь необходимый курс алгебры для 10-11 классов, включая такие сложные темы, как производные, интегралы, логарифмы и элементы математического анализа. Материал представлен последовательно и логично, что позволяет ученикам постепенно углубляться в изучение предмета. Пособие включает как теоретическую часть, так и большое количество практических заданий различного уровня сложности, что способствует закреплению знаний.

Одной из главных особенностей учебника является наличие задач повышенной сложности, которые стимулируют развитие логического мышления и навыков решения нестандартных задач. Кроме того, в книге представлены примеры из реальной жизни, что делает изучение алгебры более интересным и прикладным.

Преимущества учебника

Четкая структура материала
Учебник разделен на главы и параграфы с последовательным изложением тем. Это позволяет ученикам легко ориентироваться в содержании и возвращаться к ранее изученным темам для повторения.
Пошаговые объяснения
Каждая новая тема сопровождается подробными примерами с пошаговым решением. Это помогает ученикам лучше понять алгоритмы выполнения задач.
Разнообразие упражнений
В учебнике представлены задачи разного уровня сложности: от базовых до олимпиадных. Это делает пособие полезным как для обычных школьников, так и для тех, кто готовится к экзаменам или олимпиадам.
Практическая направленность
Включение задач из реальной жизни (например, расчет процентов или использование математических моделей) помогает ученикам видеть практическое применение алгебры.
Подготовка к ЕГЭ
Учебник содержит задания, аналогичные тем, которые встречаются на ЕГЭ, что делает его отличным инструментом для подготовки к экзаменам.

Учебник «Алгебра» Алимова для 10-11 классов – это надежный помощник в изучении математики. Он подходит как для базового освоения предмета, так и для углубленного изучения. Благодаря четкой структуре, разнообразию заданий и ориентации на экзамены, данный учебник является одним из лучших выборов для старшеклассников.

ГДЗ по Алгебре 10-11 Класс Номер 924 Алимов — Подробные Ответы

Задача

Построить эскиз графика функции у = f (х), непрерывной на отрезке [а; b], если:

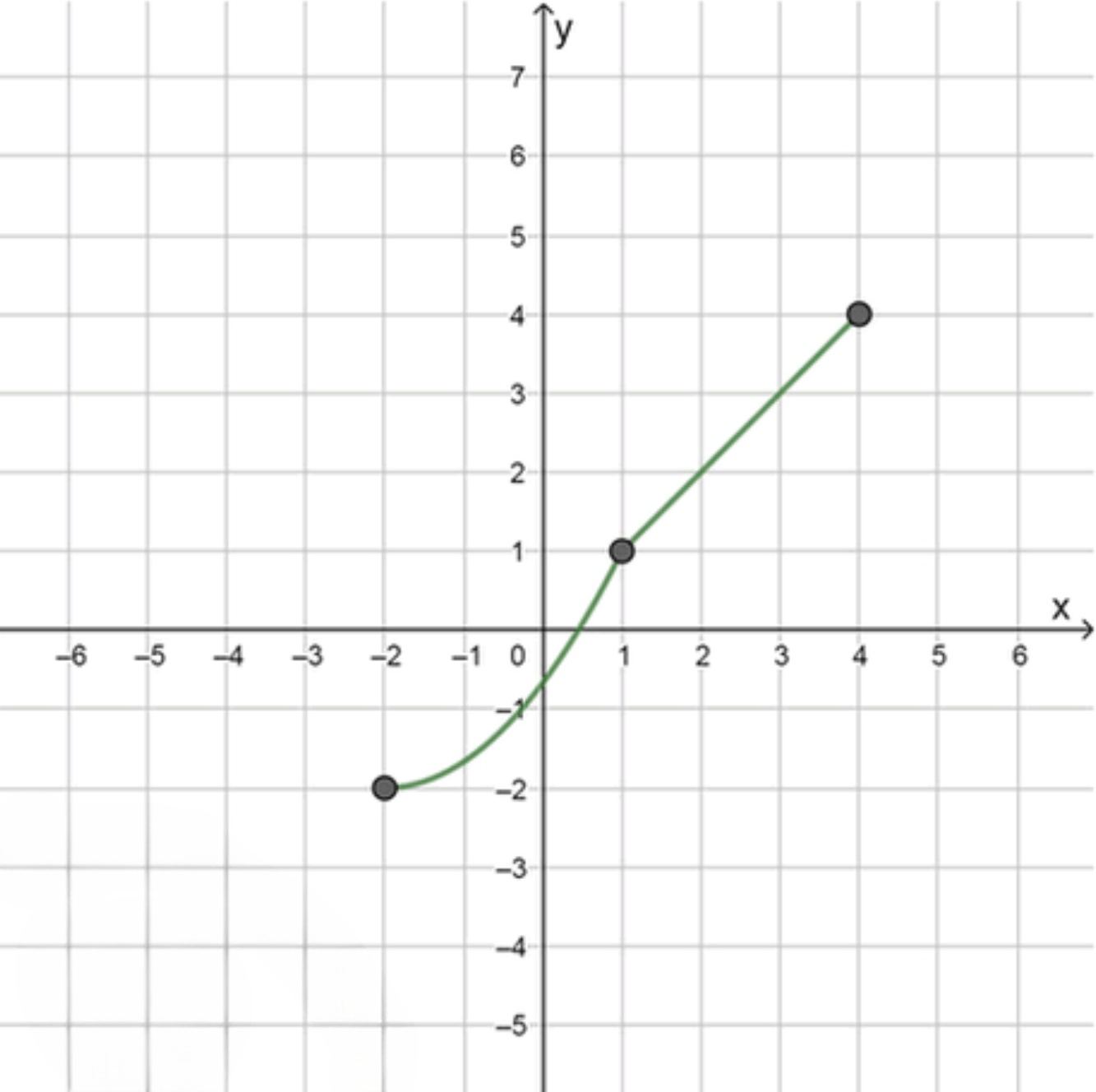
а =-2, b = 4, f (-2) =-2, у = f(x) возрастает на отрезке [-2; 1] и f(х) = x при 1 < = х < = 4;
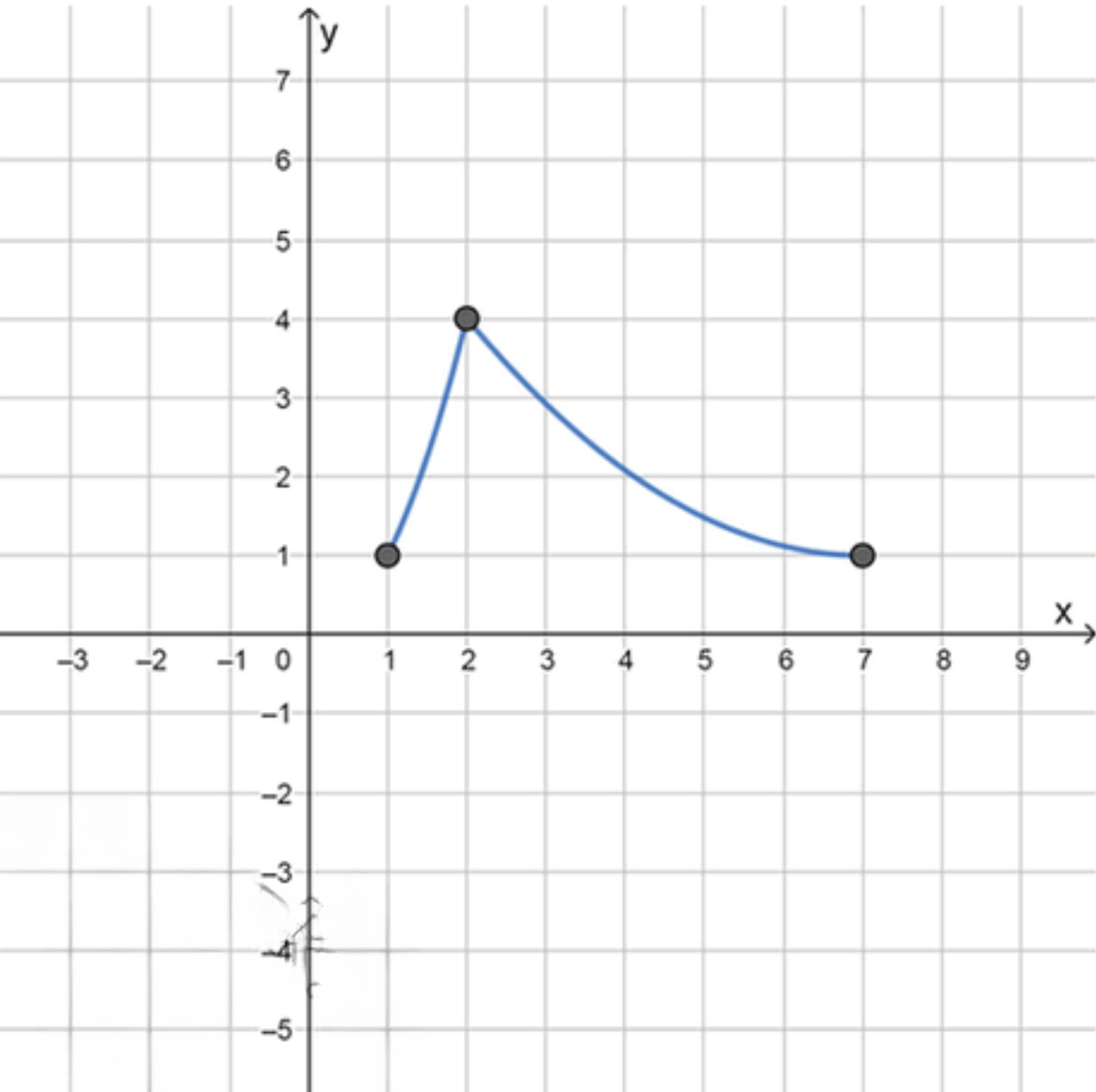
а = 1, 6 = 7, f (7) = 1, f(x) = x2 при 1 < =х > =2, у = f (х) убывает на промежутке (2; 7].

Краткий ответ:

Эскиз графика непрерывной функции, определенной на отрезке $[a; b]$ :

$1) a = - 2$ , $b = 4$ , $f (- 2) = - 2$ , $f (x) = x$ при $1 \leq x \leq 4$ ;
$y = f (x)$ возрастает на отрезке $[- 2; 1]$ ;

$2) a = 1$ , $b = 7$ , $f (7) = 1$ , $f (x) = x^{2}$ при $1 \leq x \leq 2$ ;
$y = f (x)$ убывает на промежутке $(2; 7]$ ;

Подробный ответ:

Задача 1:

Эскиз графика непрерывной функции, определенной на отрезке $[a; b]$ :

$a = - 2$ , $b = 4$ , $f (- 2) = - 2$ , $f (x) = x$ при $1 \leq x \leq 4$ ;
$y = f (x)$ возрастает на отрезке $[- 2; 1]$ ;

Разбор 1:

Для начала разберем, что происходит на этом участке:

Отрезок: Нам даны значения для $a = - 2$ и $b = 4$ , то есть функция определена на интервале от $- 2$ до $4$ .
Граничные условия: У нас есть также граничные значения для $f (x)$ , при которых $f (- 2) = - 2$ . Это означает, что значение функции в точке $x = - 2$ равно $- 2$ .
Функция $f (x) = x$ на интервале $1 \leq x \leq 4$ : Это линейная функция, которая определена на интервале от 1 до 4. Поэтому, на этом участке, функция растет, так как для линейной функции с угловым коэффициентом равным 1, значение функции увеличивается с увеличением $x$ .
Возрастает на отрезке $[- 2; 1]$ : Это ключевая информация, которая дает нам понять, что функция имеет положительный наклон на интервале от $- 2$ до 1. Мы знаем, что функция возрастает на этом интервале, и можем сделать вывод, что функция будет иметь положительный наклон на отрезке $[- 2; 1]$ .

Итог для первого случая:

Функция $f (x)$ определяется на отрезке $[- 2; 4]$ , но известно, что она линейна и растет на интервале от $- 2$ до $1$ . На интервале от 1 до 4 функция имеет вид $f (x) = x$ , то есть это просто прямая с угловым коэффициентом 1.

Задача 2:

$a = 1$ , $b = 7$ , $f (7) = 1$ , $f (x) = x^{2}$ при $1 \leq x \leq 2$ ;
$y = f (x)$ убывает на промежутке $(2; 7]$ ;

Разбор 2:

Теперь перейдем ко второму случаю:

Отрезок: Функция определяется на отрезке от $a = 1$ до $b = 7$ , то есть на интервале $[1, 7]$ .
Граничные условия: Мы знаем, что $f (7) = 1$ , то есть значение функции в точке $x = 7$ равно 1.
Функция $f (x) = x^{2}$ на интервале $1 \leq x \leq 2$ : Это квадратичная функция, которая имеет положительную кривизну (парабола). На интервале от 1 до 2 функция растет, так как для квадратичной функции с положительным коэффициентом при $x^{2}$ , график будет увеличиваться, начиная от $x = 1$ до $x = 2$ .
Убывает на промежутке $(2; 7]$ : На этом участке функция убывает. Это важное замечание, потому что квадратичная функция $f (x) = x^{2}$ возрастает на интервале $1 \leq x \leq 2$ , но на отрезке $(2; 7]$ функция будет иметь отрицательный наклон, поскольку на отрезке от 2 до 7 вторая производная будет отрицательной. Это означает, что функция убывает на данном промежутке.

Итог для второго случая:

Функция $f (x)$ на отрезке $[1; 7]$ состоит из двух частей: на отрезке $[1, 2]$ функция является квадратичной и возрастает, а на отрезке $(2, 7]$ функция убывает.

Оцени решение

← Предыдущий Следующий →

Сообщить об ошибке

Задачи для внеклассной работы