ГДЗ по Алгебре 10-11 Класс Номер 921 Алимов — Подробные Ответы

Построить эскиз графика функции у = f (х), непрерывной на отрезке [а; b], если:

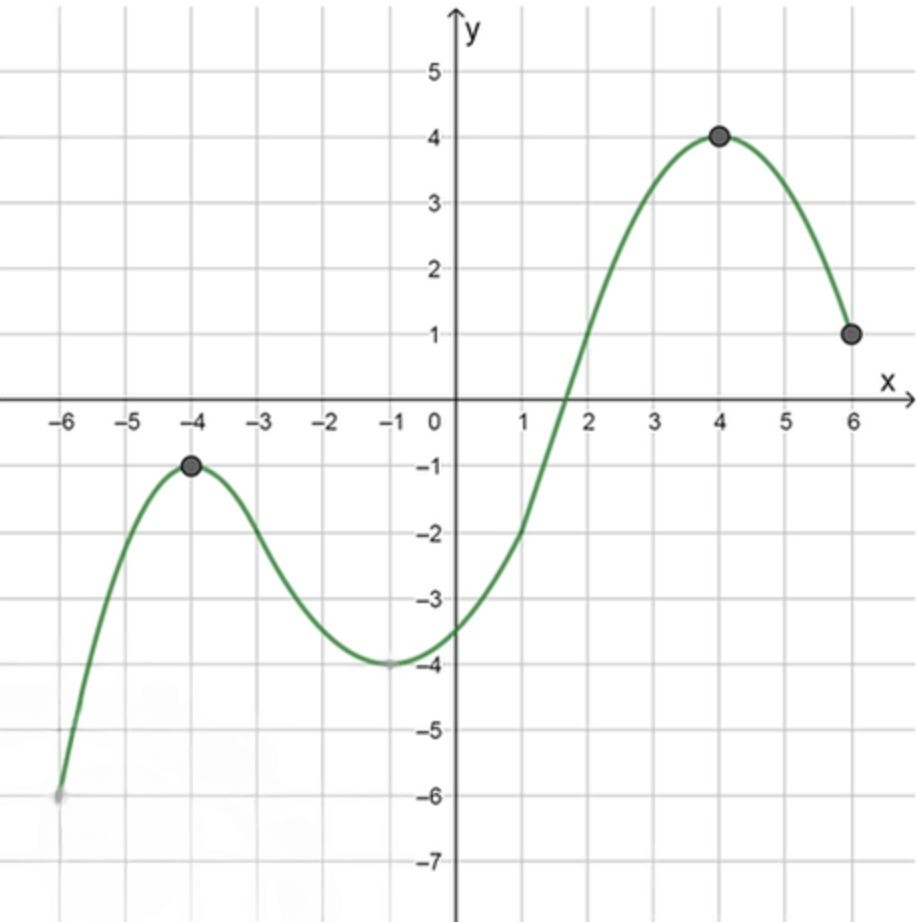
1. а =-6, b = 6, f(-6) = -6, f(6) = 1, f'(x) > 0 при -6 < х < -4, -1 < х < 4, f'(x) < 0 при -4 < х < -1, 4 < х < 6, f'(-4) = 0, f'(-1) = О, f'(4) = 0;
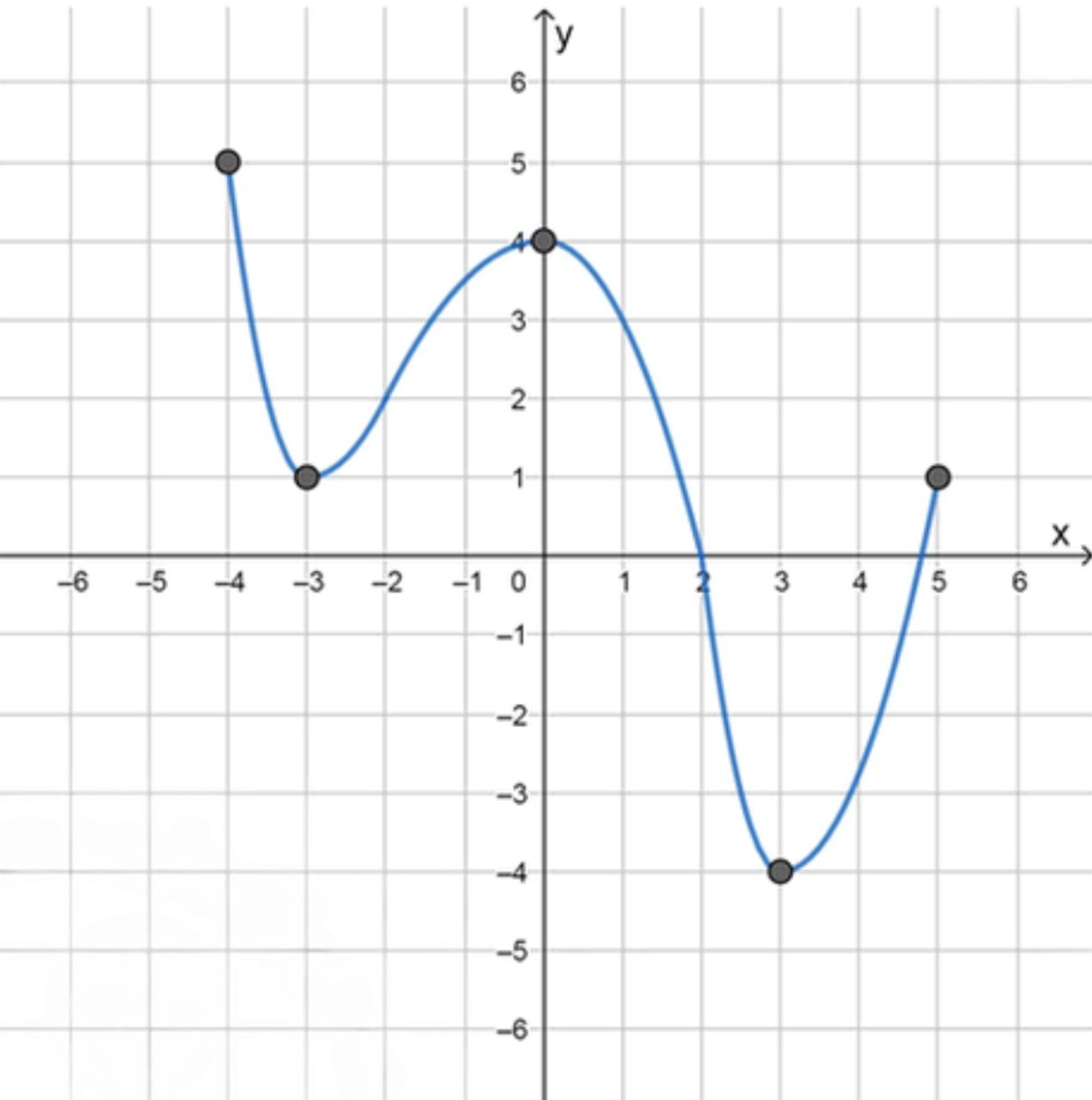
2. а = -4, b = 5,f (-4) = 5, f(5) = 1, f'(x) < 0 при -4 < х < -3, 0 < х < 3, f'(х) > 0 при -3 < х < О, 3 < х < 5, f'(-3) = 0, f'(0) = 0, f'(3) = 0.

Эскиз графика непрерывной функции, определенной на отрезке $[a;b]$:

$\mathrm{1)\; a}=-6$, $b=6$, $f(-6)=-6$, $f(6)=1$;
$f^{\mathrm{\prime }}(-4)=0$, $f^{\mathrm{\prime }}(-1)=0$, $f^{\mathrm{\prime }}(4)=0$;
$f^{\mathrm{\prime }}(x)>0$ при $-6<x<-4$, $-1<x<4$;
$f^{\mathrm{\prime }}(x)<0$ при $-4<x<-1$, $4<x<6$;

$\mathrm{2)\; a}=-4$, $b=5$, $f(-4)=5$, $f(5)=1$;
$f^{\mathrm{\prime }}(-3)=0$, $f^{\mathrm{\prime }}(0)=0$, $f^{\mathrm{\prime }}(3)=0$;
$f^{\mathrm{\prime }}(x)<0$ при $-4<x<-3$, $0<x<3$;
$f^{\mathrm{\prime }}(x)>0$ при $-3<x<0$, $3<x<5$;

1. График функции на отрезке $[a;b]$

1.1. Дано:

• Отрезок $[a;b]=[-6;6]$.
• Значения функции на концах отрезка:
  • $f(-6)=-6$
  • $f(6)=1$
• Даны точки, в которых производная равна нулю:
  • $f^{\mathrm{\prime }}(-4)=0$
  • $f^{\mathrm{\prime }}(-1)=0$
  • $f^{\mathrm{\prime }}(4)=0$
• Даны интервалы, на которых производная больше или меньше нуля:
  • $f^{\mathrm{\prime }}(x)>0$ при $-6<x<-4$ и $-1<x<4$
  • $f^{\mathrm{\prime }}(x)<0$ при $-4<x<-1$ и $4<x<6$

1.2. Как интерпретировать информацию:

Значения функции на концах интервала:

• $f(-6)=-6$ и $f(6)=1$. Это говорит нам, что функция на отрезке $[-6;6]$ начинается в точке $(-6,-6)$ и заканчивается в точке $(6,1)$.

Важно заметить, что функция непрерывна, то есть она не имеет разрывов. Это важно для дальнейшего анализа поведения функции на этом отрезке.

Производная равна нулю в точках:

• $f^{\mathrm{\prime }}(-4)=0$, $f^{\mathrm{\prime }}(-1)=0$, $f^{\mathrm{\prime }}(4)=0$. Это означает, что в точках $x=-4,-1,4$ касательные к графику функции горизонтальны (наклон касательной равен нулю). Такие точки называются критическими точками, в которых функция может достигать локальных экстремумов (минимумов или максимумов).

Знаки производной на интервалах:

• $f^{\mathrm{\prime }}(x)>0$ при $-6<x<-4$ и $-1<x<4$. Это означает, что на этих интервалах функция возрастает, то есть график функции поднимается слева направо.
• $f^{\mathrm{\prime }}(x)<0$ при $-4<x<-1$ и $4<x<6$. Это означает, что на этих интервалах функция убывает, то есть график функции спускается слева направо.

1.3. Построение графика:

На основе этих характеристик можем построить эскиз графика функции:

• На интервале $-6<x<-4$ функция возрастает, начиная с точки $(-6,-6)$.
• В точке $x=-4$ производная равна нулю, и функция достигает локального минимума.
• На интервале $-4<x<-1$ функция убывает.
• В точке $x=-1$ производная снова равна нулю, и функция достигает локального максимума.
• На интервале $-1<x<4$ функция снова возрастает.
• В точке $x=4$ производная равна нулю, и функция достигает локального минимума.
• На интервале $4<x<6$ функция убывает, достигая значения $f(6)=1$.

График функции будет иметь три экстремума в точках $x=-4,-1,4$, два локальных минимума и один локальный максимум.

2. График функции на отрезке $[a;b]$

2.1. Дано:

• Отрезок $[a;b]=[-4;5]$.
• Значения функции на концах отрезка:
  • $f(-4)=5$
  • $f(5)=1$
• Даны точки, в которых производная равна нулю:
  • $f^{\mathrm{\prime }}(-3)=0$
  • $f^{\mathrm{\prime }}(0)=0$
  • $f^{\mathrm{\prime }}(3)=0$
• Даны интервалы, на которых производная больше или меньше нуля:
  • $f^{\mathrm{\prime }}(x)<0$ при $-4<x<-3$ и $0<x<3$
  • $f^{\mathrm{\prime }}(x)>0$ при $-3<x<0$ и $3<x<5$

2.2. Как интерпретировать информацию:

Значения функции на концах интервала:

• $f(-4)=5$ и $f(5)=1$. Это говорит нам, что функция начинается в точке $(-4,5)$ и заканчивается в точке $(5,1)$.

Производная равна нулю в точках:

• $f^{\mathrm{\prime }}(-3)=0$, $f^{\mathrm{\prime }}(0)=0$, $f^{\mathrm{\prime }}(3)=0$. Это означает, что в точках $x=-3,0,3$ касательные к графику функции горизонтальны (наклон касательной равен нулю). Эти точки также являются критическими.

Знаки производной на интервалах:

• $f^{\mathrm{\prime }}(x)<0$ при $-4<x<-3$ и $0<x<3$. Это означает, что на этих интервалах функция убывает.
• $f^{\mathrm{\prime }}(x)>0$ при $-3<x<0$ и $3<x<5$. Это означает, что на этих интервалах функция возрастает.

2.3. Построение графика:

• На интервале $-4<x<-3$ функция убывает.
• В точке $x=-3$ производная равна нулю, и функция достигает локального максимума.
• На интервале $-3<x<0$ функция возрастает.
• В точке $x=0$ производная равна нулю, и функция достигает локального минимума.
• На интервале $0<x<3$ функция убывает.
• В точке $x=3$ производная равна нулю, и функция достигает локального максимума.
• На интервале $3<x<5$ функция возрастает, заканчиваясь в точке $f(5)=1$

График функции будет иметь два экстремума в точках $x=-3,3$ и один локальный минимум в точке $x=0$.