Учебник «Алгебра» для 10-11 классов под авторством Алимова – это один из наиболее популярных и широко используемых учебных пособий для старшеклассников. Он заслужил признание как среди учителей, так и среди учеников благодаря своей структурированности, доступности изложения и качественной проработке материала.
Учебник охватывает весь необходимый курс алгебры для 10-11 классов, включая такие сложные темы, как производные, интегралы, логарифмы и элементы математического анализа. Материал представлен последовательно и логично, что позволяет ученикам постепенно углубляться в изучение предмета. Пособие включает как теоретическую часть, так и большое количество практических заданий различного уровня сложности, что способствует закреплению знаний.
Одной из главных особенностей учебника является наличие задач повышенной сложности, которые стимулируют развитие логического мышления и навыков решения нестандартных задач. Кроме того, в книге представлены примеры из реальной жизни, что делает изучение алгебры более интересным и прикладным.
Преимущества учебника
- Четкая структура материала
Учебник разделен на главы и параграфы с последовательным изложением тем. Это позволяет ученикам легко ориентироваться в содержании и возвращаться к ранее изученным темам для повторения. - Пошаговые объяснения
Каждая новая тема сопровождается подробными примерами с пошаговым решением. Это помогает ученикам лучше понять алгоритмы выполнения задач. - Разнообразие упражнений
В учебнике представлены задачи разного уровня сложности: от базовых до олимпиадных. Это делает пособие полезным как для обычных школьников, так и для тех, кто готовится к экзаменам или олимпиадам. - Практическая направленность
Включение задач из реальной жизни (например, расчет процентов или использование математических моделей) помогает ученикам видеть практическое применение алгебры. - Подготовка к ЕГЭ
Учебник содержит задания, аналогичные тем, которые встречаются на ЕГЭ, что делает его отличным инструментом для подготовки к экзаменам.
Учебник «Алгебра» Алимова для 10-11 классов – это надежный помощник в изучении математики. Он подходит как для базового освоения предмета, так и для углубленного изучения. Благодаря четкой структуре, разнообразию заданий и ориентации на экзамены, данный учебник является одним из лучших выборов для старшеклассников.
ГДЗ по Алгебре 10-11 Класс Номер 917 Алимов — Подробные Ответы
Построить эскиз графика непрерывной функции у = f (х), определённой на отрезке [а; b], если:
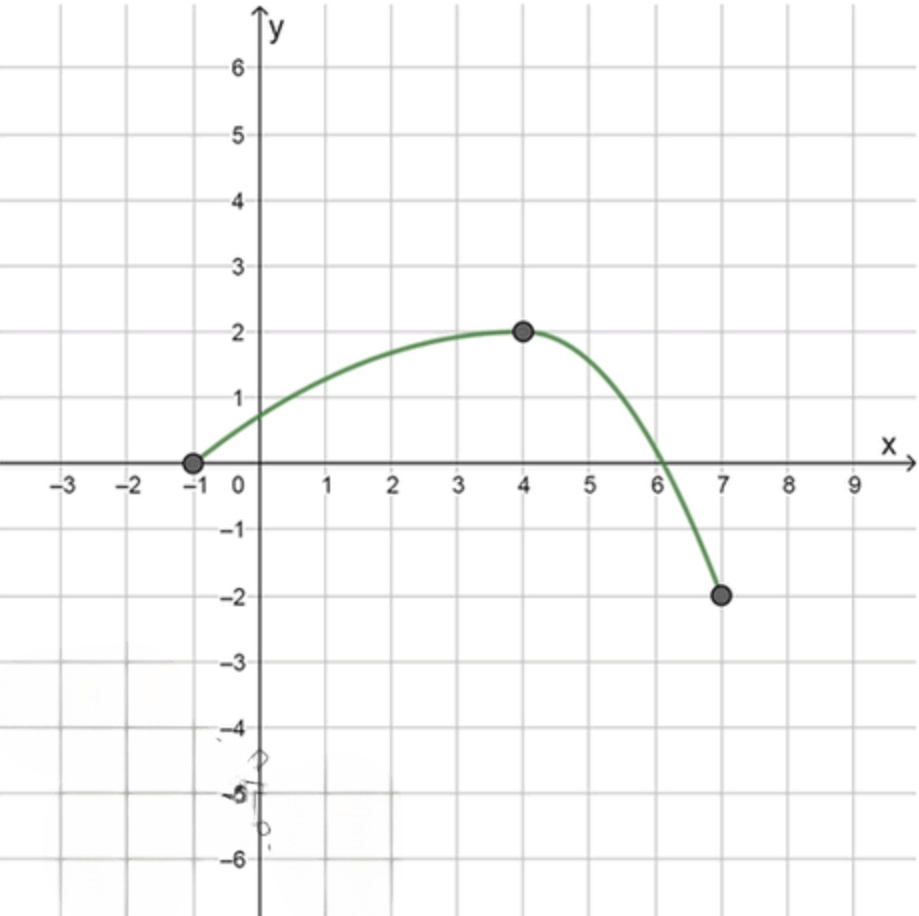
- а = -1, b = 7, f(-1) = 0, f(7) = -2, f'(x) > 0 при -1 < х < 4, f'(x) < 0 при 4 < х < 7, f'(4) = 0;
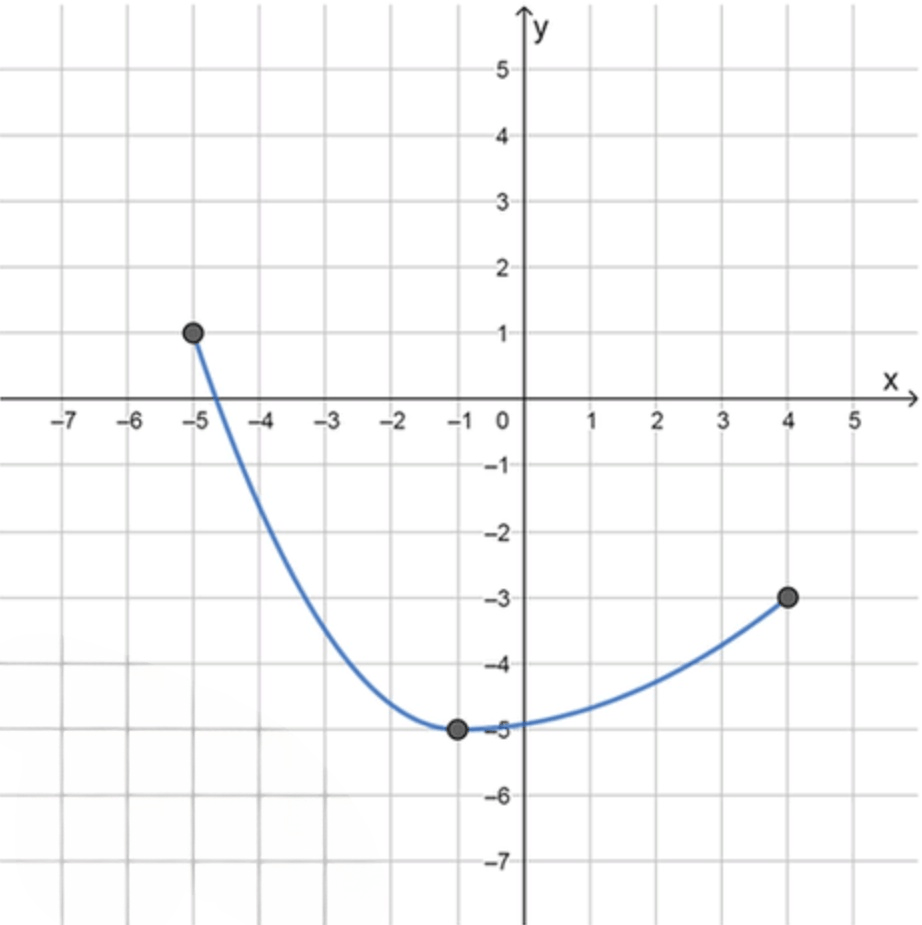
- а = -5, 6 = 4, f(-5) = 1, f(4) = -3, f'(x) < 0 при -5 < х < -1, f'(x) > 0 при -1 < х < 4, f'(-1) = 0.
Эскиз графика непрерывной функции, определенной на отрезке :
, , , , ;
при , при ;
, , , , ;
при , при ;
Для решения задачи, связанной с графиками непрерывной функции, необходимо рассмотреть различные свойства функции на отрезке , а также поведение её производной. Рассмотрим подробное решение по каждому из пунктов.
1. Первый график: , , , , ;
при , при .
1.1. Анализ значений функции на отрезке
- Функция задана на отрезке с и .
- Важно, что на этом отрезке функция принимает значения:
- — значение функции в начале отрезка.
- — значение функции в конце отрезка.
1.2. Исследование производной
- Производная указывает на наклон касательной к графику функции.
- Из условия следует, что на касательная к графику функции горизонтальна (то есть, на этой точке функция имеет локальный экстремум — минимум или максимум).
- Также, из условия при , мы можем сделать вывод, что функция возрастает на интервале . Это означает, что значение функции на отрезке от до увеличивается.
- Условие при указывает, что на интервале функция убывает, то есть её значение уменьшается.
1.3. Поведение функции и график
- Функция начинается с , растёт до некоторого максимума, который достигается в точке , где производная равна нулю (горизонтальная касательная).
- После точки функция начинает убывать, и на конце отрезка, в точке , значение функции равно .
2. Второй график: , , , , ;
при , при .
2.1. Анализ значений функции на отрезке
- Функция задана на отрезке с и .
- Важные точки:
- — значение функции в начале отрезка.
- — значение функции в конце отрезка.
2.2. Исследование производной
- Условие указывает, что в точке функция имеет экстремум (минимум или максимум), так как касательная к графику функции горизонтальна.
- Из условия при следует, что функция убывает на интервале . Значение функции уменьшается на этом интервале.
- Условие при означает, что на интервале функция возрастает, то есть её значение увеличивается.
2.3. Поведение функции и график
- Функция начинается с , убывает на интервале , достигая минимума в точке .
- После точки функция начинает возрастать и продолжает увеличиваться до точки , где её значение равно .
Итоговый анализ
- В первом случае, на отрезке , функция возрастает до , а затем начинает убывать. Это соответствуют всем условиям задачи, включая значения функции в точках и производной.
- Во втором случае, на отрезке , функция убывает до точки , после чего начинает возрастать до . Также все условия задачи выполнены.
Графики
На графиках это будет выглядеть следующим образом:
- На первом графике начинает с , возрастает до максимума в точке , а затем убывает до .
- На втором графике начинается с , убывает до минимума в точке , а затем возрастает до .
Задачи для внеклассной работы
