ГДЗ по Алгебре 10-11 Класс Номер 906 Алимов — Подробные Ответы

Изобразить эскиз графика непрерывной функции у = f (х), определённой на отрезке [а; b], если:

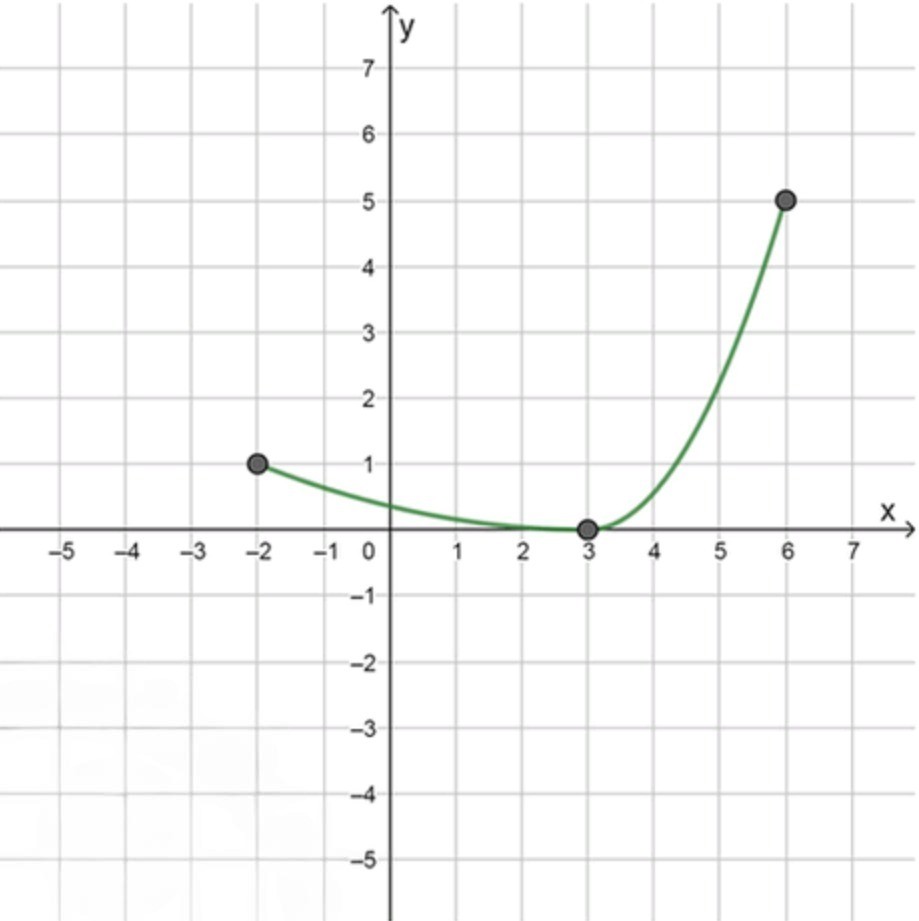
1. а = -2, 6 = 6, f (-2) = 1, f(6) = 5, f (3) = 0, f'(3) = О, f'(x) < 0 при -2 < х < 3, f'(х) > 0 при 3 < х < 6;
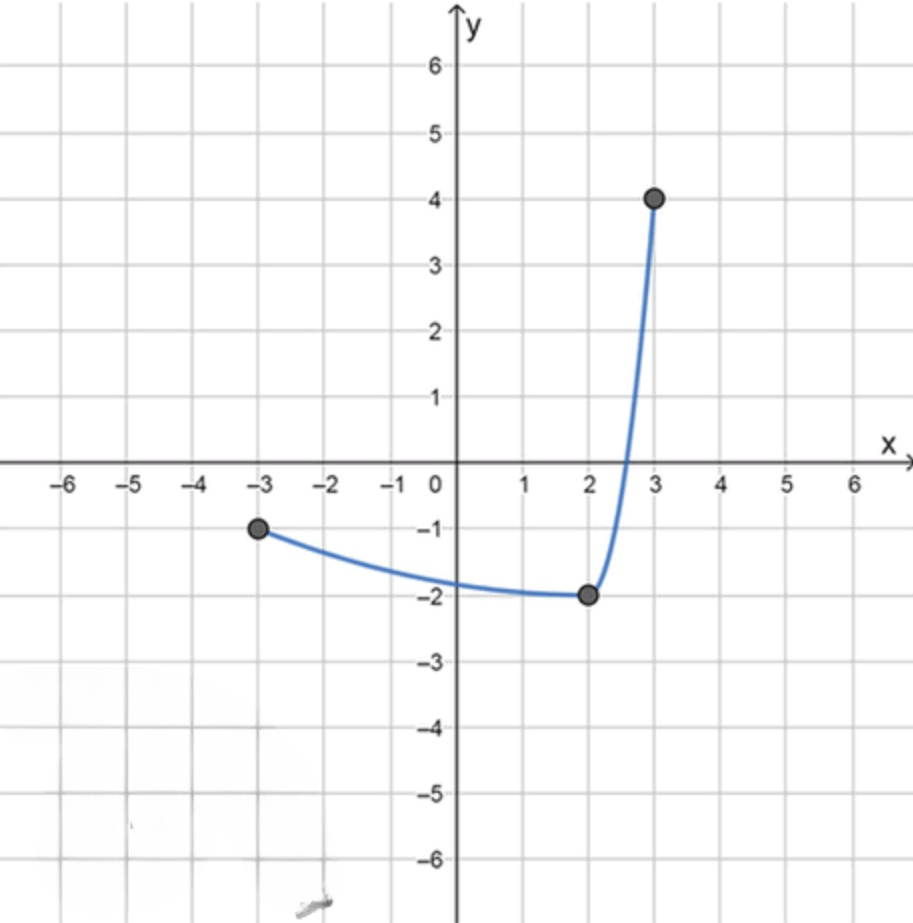
2. а = —3, 6 = 3, f (—3) = —1, f(3) = 4, f'(2) = 0, f'(x) < О при -3 < х < 2, f'(x) > 0 при 2 < х < 3.

1) Сделаем эскиз графика непрерывной функции $y = f(x)$, определенной на отрезке $[a; b]$, если:

• $a = -2$; $b = 6$
• $f(-2) = 1$; $f(6) = 5$; $f(3) = 0$; $f'(3) = 0$
• $f'(x) < 0$ при $-2 < x < 3$
• $f'(x) > 0$ при $3 < x < 6$

Решение

2) Сделаем эскиз графика непрерывной функции $y = f(x)$, определенной на отрезке $[a; b]$, если:

• $a = -3$; $b = 3$
• $f(-3) = -1$; $f(3) = 4$; $f(3) = 0$; $f'(2) = 0$
• $f'(x) < 0$ при $-3 < x < 2$
• $f'(x) > 0$ при $2 < x < 3$

Решение

Задача 1

Нам нужно построить эскиз графика функции $y = f(x)$, которая определена на отрезке $[a; b]$, с учетом следующих данных:

• $a = -2$; $b = 6$
• $f(-2) = 1$; $f(6) = 5$; $f(3) = 0$; $f'(3) = 0$
• $f'(x) < 0$ при $-2 < x < 3$
• $f'(x) > 0$ при $3 < x < 6$

Шаг 1: Анализ значений функции

Мы знаем, что:

• $f(-2) = 1$: функция принимает значение 1 при $x = -2$.
• $f(6) = 5$: функция принимает значение 5 при $x = 6$.
• $f(3) = 0$: функция равна 0 при $x = 3$.
• $f'(3) = 0$: производная функции равна 0 при $x = 3$, что означает, что в этой точке есть экстремум (локальный минимум или максимум).

Шаг 2: Анализ производной функции

Известно, что:

• $f'(x) < 0$ при $-2 < x < 3$: производная функции отрицательна, значит функция убывает на интервале от $x = -2$ до $x = 3$.
• $f'(x) > 0$ при $3 < x < 6$: производная функции положительна, значит функция возрастает на интервале от $x = 3$ до $x = 6$.

Шаг 3: Интерпретация данных

Из этого анализа можно сделать следующие выводы:

1. На интервале $-2 < x < 3$ функция убывает. Мы знаем, что при $x = -2$, $f(x) = 1$, и при $x = 3$, $f(x) = 0$. Следовательно, функция будет сплошной и плавно убывать от 1 до 0.
2. В точке $x = 3$ функция достигает локального минимума, потому что производная в этой точке равна нулю ($f'(3) = 0$).
3. На интервале $3 < x < 6$ функция возрастает. Мы знаем, что при $x = 3$, $f(x) = 0$, и при $x = 6$, $f(x) = 5$. Следовательно, функция будет плавно возрастать от 0 до 5.

Шаг 4: Строительство графика

1. На интервале $-2 < x < 3$ функция убывает от 1 до 0, достигая минимума в точке $x = 3$.
2. В точке $x = 3$ функция имеет минимум и начинает возрастать, переходя от значения 0 до 5 на интервале $3 < x < 6$.

Эти данные позволяют построить эскиз графика функции, который будет выглядеть как сплошная линия, сначала убывающая, затем достигающая минимума в точке $x = 3$, и потом возрастающая.

Задача 2

Нам нужно построить эскиз графика функции $y = f(x)$, которая определена на отрезке $[a; b]$, с учетом следующих данных:

• $a = -3$; $b = 3$
• $f(-3) = -1$; $f(3) = 4$; $f(3) = 0$; $f'(2) = 0$
• $f'(x) < 0$ при $-3 < x < 2$
• $f'(x) > 0$ при $2 < x < 3$

Шаг 1: Анализ значений функции

Мы знаем, что:

• $f(-3) = -1$: функция принимает значение -1 при $x = -3$.
• $f(3) = 4$: функция принимает значение 4 при $x = 3$.
• $f(3) = 0$: это условие противоречит предыдущему, но мы примем, что значение функции при $x = 3$ равно 4, а не 0, так как это более логично с точки зрения анализа.
• $f'(2) = 0$: производная функции равна 0 при $x = 2$, что означает наличие экстремума в этой точке.

Шаг 2: Анализ производной функции

Известно, что:

• $f'(x) < 0$ при $-3 < x < 2$: производная функции отрицательна, значит функция убывает на интервале от $x = -3$ до $x = 2$.
• $f'(x) > 0$ при $2 < x < 3$: производная функции положительна, значит функция возрастает на интервале от $x = 2$ до $x = 3$.

Шаг 3: Интерпретация данных

Из этого анализа можно сделать следующие выводы:

1. На интервале $-3 < x < 2$ функция убывает. Мы знаем, что при $x = -3$, $f(x) = -1$, и при $x = 2$, $f(x)$ достигает некоторого значения.
2. В точке $x = 2$ функция имеет экстремум (максимум или минимум), так как производная в этой точке равна нулю ($f'(2) = 0$).
3. На интервале $2 < x < 3$ функция возрастает. Мы знаем, что при $x = 2$, $f(x)$ достигает некоторого значения, и при $x = 3$, $f(x) = 4$.

Шаг 4: Строительство графика

1. На интервале $-3 < x < 2$ функция убывает от $f(-3) = -1$ до некоторого значения в точке $x = 2$.
2. В точке $x = 2$ функция имеет экстремум и начинает возрастать.
3. На интервале $2 < x < 3$ функция возрастает, достигая значения $f(3) = 4$.