ГДЗ по Алгебре 10-11 Класс Номер 901 Алимов — Подробные Ответы

Построить эскиз графика непрерывной функции у — f (х), определённой на отрезке [а; b], если:

1. а = 0, b = 5, f'(x) > 0 при 0 < х < 5, f (1) = 0, f(5) = 3;
2. а = -1, b = 3, f'(x) < 0 при -1 < х < 3, f (0) = 0, f (3) = -4.

Эскиз графика непрерывной функции, определенной на отрезке $[a; b]$:

$a = 0$, $b = 5$, $f'(x) > 0$ при $0 < x < 5$, $f(1) = 0$, $f(5) = 3$;

$a = -1$, $b = 3$, $f'(x) < 0$ при $-1 < x < 3$, $f(0) = 0$, $f(3) = -4$;

Нам предстоит построить эскизы графиков двух непрерывных функций, удовлетворяющих данным условиям.

Условие 1:

Пусть функция $y = f(x)$ определена на отрезке $[0; 5]$ с условиями:

1. $f'(x) > 0$ при $0 < x < 5$, что означает, что функция возрастает на этом отрезке.
2. $f(1) = 0$, то есть точка на графике функции при $x = 1$ имеет значение $y = 0$.
3. $f(5) = 3$, то есть точка на графике функции при $x = 5$ имеет значение $y = 3$.

Анализ условия 1:

• Функция возрастает на всём отрезке $[0; 5]$ (из условия $f'(x) > 0$), то есть её график будет направлен вверх, начиная с точки $x = 0$ и заканчивая в точке $x = 5$.
• Функция имеет точку $(1, 0)$ на графике, что означает, что график будет пересекать ось абсцисс (ось $x$) в этой точке.
• К тому же, функция имеет значение 3 в точке $x = 5$, то есть в точке $(5, 3)$ график будет пересекать прямую $y = 3$.

Что мы можем сказать о поведении графика функции?

1. Функция начинает с некоторого значения $y = f(0)$, но точно это значение не указано, так как известно только поведение функции на отрезке от 0 до 5.
2. В точке $x = 1$ график пересекает ось $x$ в точке $(1, 0)$.
3. Функция возрастает, так как её производная положительна на всём интервале $(0, 5)$.
4. График достигает значения $y = 3$ в точке $x = 5$.

Исходя из этого, график функции будет представлять собой плавную возрастающую кривую, которая пересекает ось абсцисс в точке $x = 1$, затем продолжает возрастать, и в точке $x = 5$ имеет значение $y = 3$.

Условие 2:

Теперь рассмотрим второе условие:

1. $a = -1$, $b = 3$, $f'(x) < 0$ при $-1 < x < 3$, что означает, что функция убывает на данном отрезке.
2. $f(0) = 0$, то есть точка на графике функции при $x = 0$ имеет значение $y = 0$.
3. $f(3) = -4$, то есть точка на графике функции при $x = 3$ имеет значение $y = -4$.

Анализ условия 2:

• Функция убывает на всём отрезке $(-1, 3)$ (из условия $f'(x) < 0$), что означает, что её график будет направлен вниз.
• График пересекает ось $x$ в точке $x = 0$, то есть в точке $(0, 0)$.
• В точке $x = 3$ функция имеет значение $y = -4$, то есть в точке $(3, -4)$ график будет пересекаться с прямой $y = -4$.

Что мы можем сказать о поведении графика функции?

1. Функция начинается с некоторого значения $y = f(-1)$, но точное значение не указано, поэтому мы можем лишь предположить, что она имеет какое-то значение на оси $y$, при $x = -1$.
2. График функции убывает на интервале $(-1, 3)$.
3. Функция пересекает ось абсцисс в точке $x = 0$, то есть график проходит через точку $(0, 0)$.
4. График достигает значения $y = -4$ в точке $x = 3$, то есть в точке $(3, -4)$.

График функции будет представлять собой плавную убывающую кривую, которая начинается в некоторой точке на оси $y$ для $x = -1$, затем пересекает ось абсцисс в точке $(0, 0)$ и продолжает убывать до значения $y = -4$ в точке $x = 3$.

Эскиз графиков:

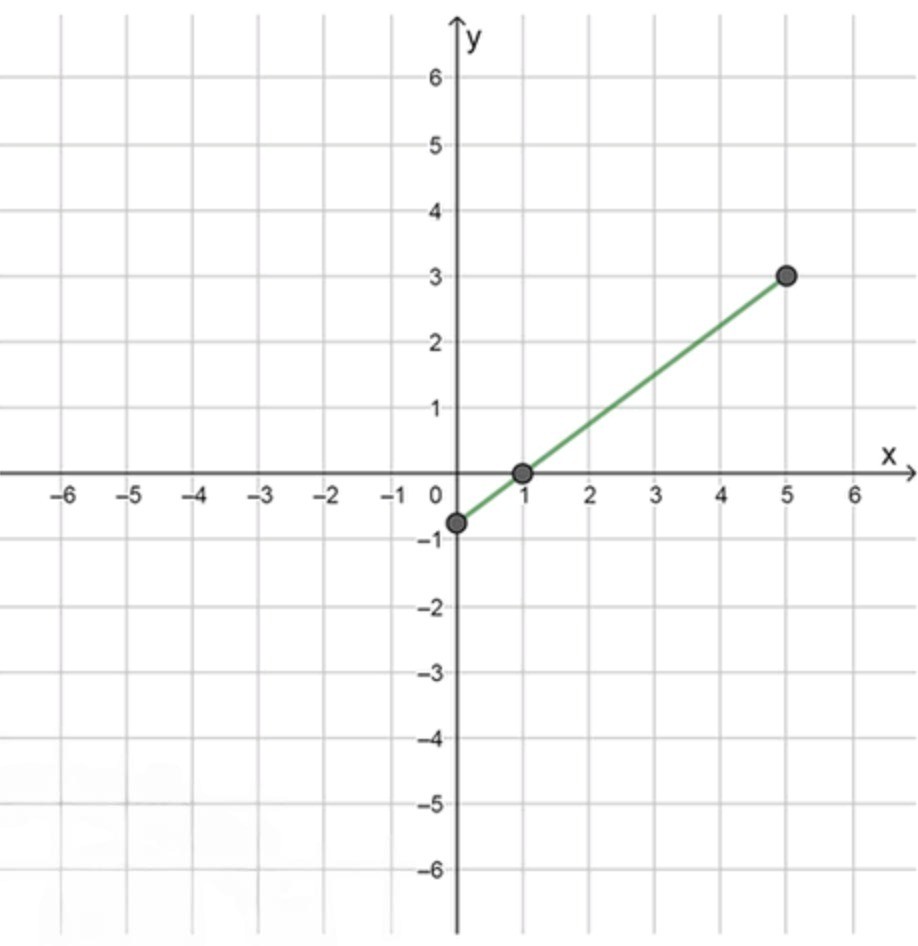
1. Для функции, определенной на отрезке $[0; 5]$:

• График возрастает на всём интервале.
• Он пересекает ось $x$ в точке $(1, 0)$.
• Он пересекает прямую $y = 3$ в точке $(5, 3)$.

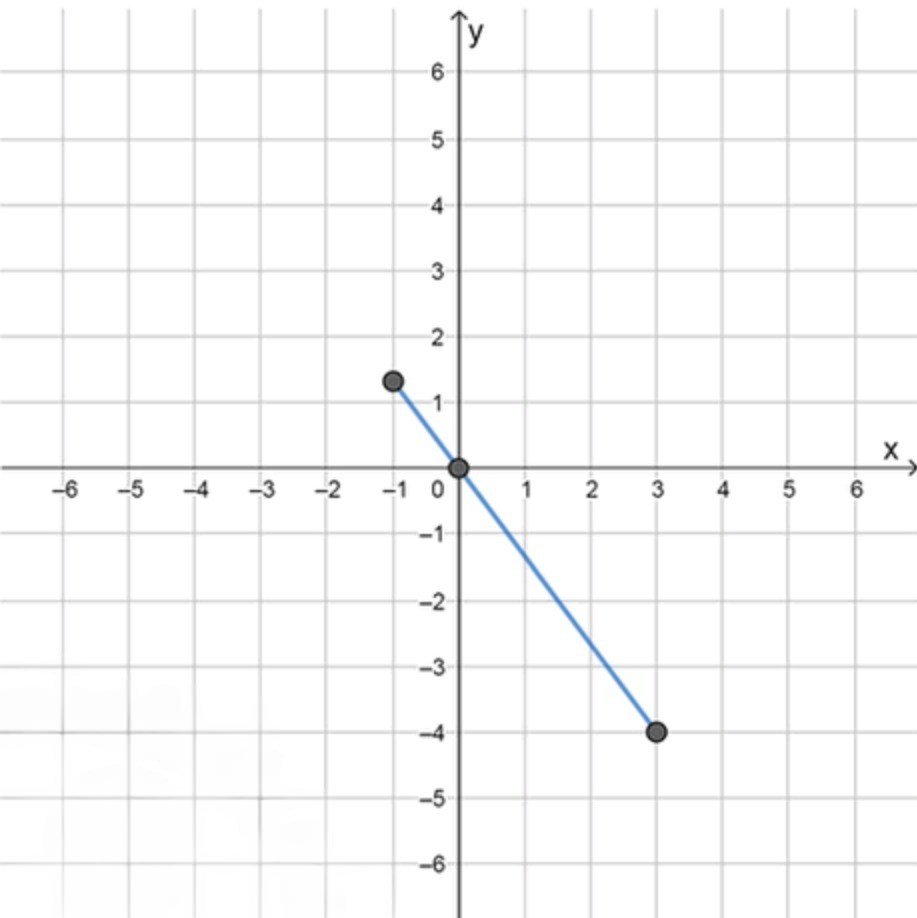
2. Для функции, определенной на отрезке $[-1; 3]$:

• График убывает на всём интервале.
• Он пересекает ось $x$ в точке $(0, 0)$.
• Он достигает значения $y = -4$ в точке $(3, -4)$.