ГДЗ по Алгебре 10-11 Класс Номер 263 Алимов — Подробные Ответы

1. y=2^(x+|x|);
2. y= |3^(|x|)-3.

$y = 2^{x + |x|}$;

• Если $x < 0$, тогда:

  $$y = 2^{x — x} = 2^0 = 1;$$

• Если $x \geq 0$, тогда:

  $$y = 2^{x + x} = 2^{2x};$$

• Область определения: $x \in \mathbb{R}$;
• Множество значений: $y > 0$;
• Функция возрастает, так как $2 > 1$;

График функции:

$y = |3^{|x|} — 3|$;

• Функция является четной:

  $$y(-x) = |3^{|-x|} — 3| = |3^{|x|} — 3| = y(x);$$

• Рассмотрим функцию $y = 3^{|x|}$:
  • Если $x \geq 0$, тогда $y = 3^x$;
  • Область определения: $x \in \mathbb{R}$;
  • Множество значений: $y > 0$;
  • Функция возрастает, так как $3 > 1$;

• Построим график функции $y = 3^x$ и осуществим его сдвиг вдоль оси ординат на 3 единицы вниз, а затем отразим его часть, находящуюся под осью абсцисс:

1) $y = 2^{x + |x|}$

Рассмотрим функцию:

$$y = 2^{x + |x|}$$

Мы видим, что выражение для функции зависит от величины $x$, а точнее, от того, является ли $x$ положительным или отрицательным, так как абсолютная величина $|x|$ изменяет поведение функции в зависимости от знака $x$.

Шаг 1: Разделим функцию на два случая

Случай 1: $x < 0$

Для отрицательных значений $x$, $|x| = -x$. Таким образом, выражение $x + |x|$ принимает вид:

$$x + |x| = x + (-x) = 0$$

Тогда функция становится:

$$y = 2^{0} = 1$$

То есть, для всех отрицательных $x$ значение функции будет равно 1.

Случай 2: $x \geq 0$

Для положительных значений $x$, $|x| = x$, и поэтому:

$$x + |x| = x + x = 2x$$

Тогда функция становится:

$$y = 2^{2x}$$

Это означает, что для всех $x \geq 0$, функция принимает вид экспоненциальной функции, которая возрастает с увеличением $x$.

Шаг 2: Область определения и множество значений

Область определения:

Поскольку абсолютная величина $|x|$ существует для любого $x \in \mathbb{R}$, то область определения функции:

$$x \in \mathbb{R}$$

Множество значений:

Поскольку $2^0 = 1$ и $2^{2x} > 0$ для всех $x$, то множество значений функции всегда положительное:

$$y > 0$$

Шаг 3: Поведение функции

Возрастает ли функция?

• Для $x < 0$ функция всегда равна 1, то есть постоянна.
• Для $x \geq 0$ функция имеет вид $y = 2^{2x}$, которая возрастает, так как основание 2 больше 1. Таким образом, функция будет возрастать при увеличении $x$ в области $x \geq 0$.

Шаг 4: Пример таблицы значений

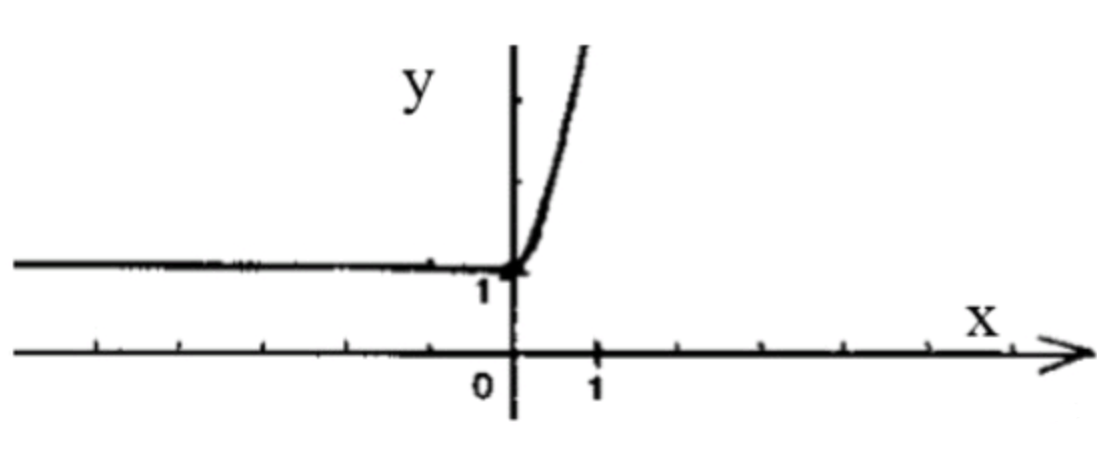
Шаг 5: График функции

График функции состоит из двух частей:

• Для $x < 0$ функция постоянна и равна 1.
• Для $x \geq 0$ функция растет экспоненциально, как $y = 2^{2x}$.

2) $y = |3^{|x|} — 3|$

Рассмотрим функцию:

$$y = |3^{|x|} — 3|$$

Эта функция состоит из двух частей: экспоненциального выражения и абсолютного значения. Разберемся, как она ведет себя при различных значениях $x$.

Шаг 1: Анализ четности функции

Четность функции — это свойство, когда для любого $x$ выполняется:

$$y(-x) = y(x)$$

Рассмотрим, что происходит с функцией при замене $x$ на $-x$:

$$y(-x) = |3^{|-x|} — 3| = |3^{|x|} — 3| = y(x)$$

Таким образом, функция является четной, то есть график функции симметричен относительно оси $y$.

Шаг 2: Рассмотрим функцию $y = 3^{|x|}$

Теперь рассмотрим функцию $y = 3^{|x|}$. Для разных значений $x$ получаем:

• Если $x \geq 0$, то $y = 3^x$, и функция возрастает, так как основание 3 больше 1.
• Если $x < 0$, то $|x| = -x$, и функция все равно выражается как $y = 3^{|x|} = 3^{-x}$, что также возрастает, поскольку $y = 3^x$ для положительных значений $x$.

Таким образом, для всех $x \in \mathbb{R}$ функция $y = 3^{|x|}$ всегда возрастает при увеличении $|x|$.

Шаг 3: Область определения и множество значений

Область определения:

Поскольку абсолютная величина существует для любого $x \in \mathbb{R}$, область определения функции:

$$x \in \mathbb{R}$$

Множество значений:

Функция $3^{|x|}$ всегда положительна, так как $3^{|x|} > 0$ для любого $x$, и после вычитания 3 мы получаем выражение $3^{|x|} — 3$, которое будет всегда положительным или равным нулю. После применения абсолютной величины:

$$y \geq 0$$

Таким образом, множество значений функции:

$$y \geq 0$$

Шаг 4: Пример таблицы значений

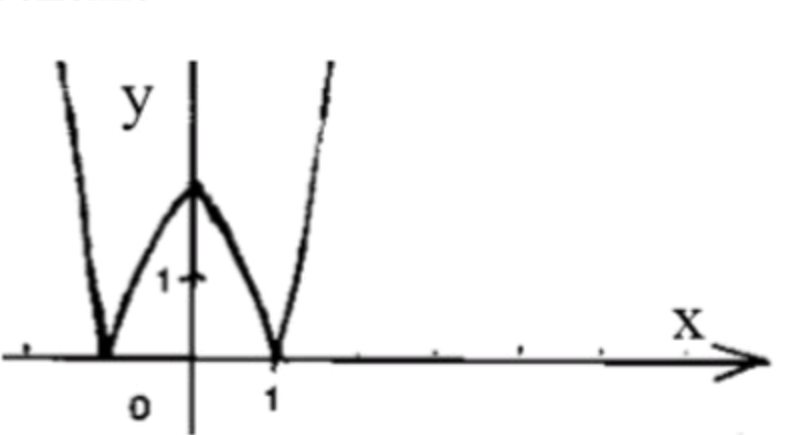
Шаг 5: Построение графика функции

• Сначала строим график функции $y = 3^{|x|}$, который является симметричным относительно оси $y$ и возрастает как экспоненциальная функция.
• Затем сдвигаем его вдоль оси ординат на 3 единицы вниз (вычитание 3).
• После этого отражаем часть графика, которая оказывается ниже оси абсцисс, по этой оси, применяя абсолютную величину.

Таким образом, график функции будет выглядеть как симметричная кривая с минимумом в точке $x = 0$, где $y = 0$, и будет расти экспоненциально по мере удаления от оси $y$.