ГДЗ по Алгебре 10-11 Класс Номер 26 Алимов — Подробные Ответы

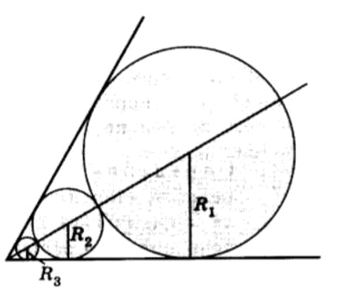
В угол, равный 60°, последовательно вписаны окружности касающиеся друг друга (рис. 5, б). Радиус первой окружности равен R1 Найти радиусы R2, R3, …, Rn, … остальных окружностей и показать, что они образуют бесконечно убывающую геометрическую прогрессию. Доказать, что сумма R1 + 2 (R2 + R3 + … + Rn + …) равна расстоянию от центра первой окружности до вершины угла.

Известно, что в угол равный 60°, последовательно вписаны окружности, касающиеся друг друга. Радиус первой окружности равен $R_1$.

Найдем радиусы $R_2, R_3, …, R_n, …$ остальных окружностей и покажем, что они образуют бесконечно убывающую геометрическую прогрессию. Докажем, что сумма $R_1 + 2(R_2 + R_3 + … + R_n + \cdots)$ равна расстоянию от центра первой окружности до вершины угла.

Решение

Расстояние от точки касания первой окружности со второй есть сумма бесконечно убывающей прогрессии диаметров окружностей с радиусами $R_2, R_3, …, R_n, …$, то есть $2(R_2 + R_2 + \cdots + R_2 + \cdots)$, а, значит, расстояние от центра первой окружности до вершины угла равно:

$$R_1 + 2(R_2 + R_2 + \cdots + R_2 + \cdots).$$

Расстояние от вершины угла до центра первой окружности равно:

$$R_1 \cdot \sin 30° = R_1 \cdot \frac{1}{2} = 2R_1.$$

Расстояние от вершины угла до центра второй окружности равно

$$2R_1 — R_2 — R_1 = R_1 — R_2.$$

Из подобия треугольника следует:

$$\frac{R_1}{R_2} = \frac{2R_1}{R_1 — R_2}.$$

Откуда

$$2R_1^2 — R_1 R_2 = 2R_1 R_2.$$

$$R_2 = \frac{R_1}{3}.$$

Аналогично

$$R_3 = \frac{R_2}{3} = \frac{R_1}{9}.$$

Тогда

$$R_n = \frac{R_1}{3^{n-1}}.$$

Что и требовалось доказать.

Условие

В угол, равный $60^\circ$, последовательно вписаны окружности, касающиеся друг друга. Радиус первой окружности равен $R_1$. Требуется:

1. Найти радиусы
   $R_2,R_3,\mathrm{.}\mathrm{.}\mathrm{.},R_n,\mathrm{.}\mathrm{.}\mathrm{. }$$\mathrm{<span\; style="font-family:\; Georgia,\; \text{'}Times\; New\; Roman\text{'},\; \text{'}Bitstream\; Charter\text{'},\; Times,\; serif;">последующих\; окружностей.</span>}$
2. Доказать, что они образуют бесконечно убывающую геометрическую прогрессию.
3. Доказать, что сумма $R_1 + 2(R_2 + R_3 + \dots + R_n + \dots)$ равна расстоянию от центра первой окружности до вершины угла.

Шаг 1: Анализ расположения окружностей

Рассмотрим две соседние окружности с центрами $O_n$ и $O_{n+1}$:

• Радиусы этих окружностей равны $R_n$$R_n$ и $R_{n+1}$.
• Окружности касаются друг друга, а также сторон угла.
• Центры окружностей лежат на биссектрисе угла.

На рисунке изображено расположение окружностей:

Шаг 2: Выражение радиусов через геометрическую прогрессию

Рассмотрим первое расстояние между центрами окружностей. Пусть первая окружность касается сторон угла в точках $A_1$ и $A_2$, а вторая в точках $A_2$ и $A_3$.

Рассчитаем расстояние от вершины угла до центра первой окружности:

$$d_1 = R_1 \cdot \frac{1}{\sin 30^\circ} = 2 R_1.$$

Теперь вычислим расстояние до центра второй окружности:

$$d_2 = d_1 — (R_1 + R_2).$$

Из подобия треугольников:

$$\frac{R_1}{R_2} = \frac{2R_1}{R_1 — R_2}.$$

Решая это уравнение, получаем:

$$R_2 = \frac{R_1}{3}.$$

Аналогично, для следующих окружностей:

$$R_3 = \frac{R_2}{3} = \frac{R_1}{9}.$$

Обобщая, получаем формулу для радиуса $n$-й окружности:

$$R_n = \frac{R_1}{3^{n-1}}.$$

Таким образом, радиусы образуют бесконечно убывающую геометрическую прогрессию с первым членом$R_1$ и знаменателем $q = \frac{1}{3}$.

Шаг 3: Вычисление суммы бесконечного ряда

Сумма бесконечно убывающей геометрической прогрессии рассчитывается по формуле:

$$S = \frac{a}{1 — q}.$$

Для суммирования радиусов окружностей:

$$S_R = R_2 + R_3 + R_4 + \dots = \frac{R_1 / 3}{1 — 1/3} = \frac{R_1 / 3}{2/3} = \frac{R_1}{2}.$$

Подставляя в выражение:

$$R_1 + 2 S_R = R_1 + 2 \cdot \frac{R_1}{2} = R_1 + R_1 = 2 R_1.$$

А это именно расстояние от центра первой окружности до вершины угла.

Вывод

1. Радиусы окружностей образуют бесконечно убывающую геометрическую прогрессию с первым членом
   $R_1$ и знаменателем $\frac{1}{3}$.
2. Сумма $R_1 + 2(R_2 + R_3 + \dots + R_n + \dots)$ действительно равна расстоянию от центра первой окружности до вершины угла.
3. Задача полностью решена и доказана.