ГДЗ по Алгебре 10-11 Класс Номер 257 Алимов — Подробные Ответы

1. у = 3х — 1;
2. у = 3^(x-1);
3. у =2^(2-x) + 3.

1)
$y = 3^x — 1;$
Рассмотрим функцию $y = 3^x$:

• Область определения: $x \in \mathbb{R}$;
• Множество значений: $y > 0$;
• Функция возрастает, так как $3 > 1$;

$$\begin{array}{|c|c|c|c|} \hline x & 0 & 1 & 2 \\ \hline y & 1 & 3 & 9 \\ \hline \end{array}$$

Построим график функции $y = 3^x$ и осуществим его сдвиг вдоль оси ординат на одну единицу вниз:

2)
$y = 3^{x-1};$
Рассмотрим функцию $y = 3^x$:

• Область определения: $x \in \mathbb{R}$;
• Множество значений: $y > 0$;
• Функция возрастает, так как $3 > 1$;

$$\begin{array}{|c|c|c|c|} \hline x & 0 & 1 & 2 \\ \hline y & 1 & 3 & 9 \\ \hline \end{array}$$

Построим график функции $y = 3^x$ и осуществим его сдвиг вдоль оси абсцисс на 1 единицу вправо:

3)
$y = 2^{2-x} + 3 = \left( \frac{1}{2} \right)^{x-2} + 3;$
Рассмотрим функцию $y = \left( \frac{1}{2} \right)^x$:

• Область определения: $x \in \mathbb{R}$;
• Множество значений: $y > 0$;
• Функция убывает, так как $0 < \frac{1}{2} < 1$;

$$\begin{array}{|c|c|c|c|c|} \hline x & -3 & -2 & -1 & 0 \\ \hline y & 8 & 4 & 2 & 1 \\ \hline \end{array}$$

Построим график функции $y = \left( \frac{1}{2} \right)^x$ и осуществим его сдвиг вдоль оси абсцисс на 2 единицы вправо и вдоль оси ординат на 3 единицы вверх:

1)
Уравнение:
$y = 3^x — 1$

Рассмотрим функцию $y = 3^x$:

• Область определения: $x \in \mathbb{R}$, так как экспоненциальная функция определена для всех действительных чисел.
• Множество значений: $y > 0$, так как для любого $x$ функция $y = 3^x$ всегда положительна (значения $3^x$ положительные).
• Монотонность: Функция возрастает, так как основание степени $3 > 1$, следовательно, $3^x$ растет с увеличением $x$.

Таблица значений функции $y = 3^x$:

$$\begin{array}{|c|c|c|c|} \hline x & 0 & 1 & 2 \\ \hline y & 1 & 3 & 9 \\ \hline \end{array}$$

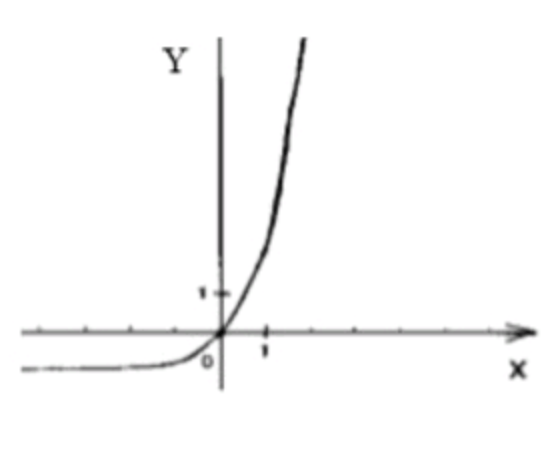
Построение графика функции $y = 3^x$:
График функции $y = 3^x$ представляет собой экспоненциальную кривую, которая проходит через точку $(0, 1)$ и растет с увеличением $x$.

Сдвиг графика вниз на одну единицу:
У нас имеется функция $y = 3^x — 1$, что означает сдвиг графика функции $y = 3^x$ на 1 единицу вниз по оси ординат.

Таким образом, график функции $y = 3^x — 1$ будет выглядеть как график функции $y = 3^x$, но на 1 единицу ниже. Все точки с координатами $(x, y)$ на графике функции $y = 3^x$ будут перемещены в точку $(x, y-1)$.

2)
Уравнение:
$y = 3^{x-1}$

Рассмотрим функцию $y = 3^x$:

• Область определения: $x \in \mathbb{R}$.
• Множество значений: $y > 0$.
• Монотонность: Функция возрастает, так как основание степени $3 > 1$.

Таблица значений функции $y = 3^x$:

$$\begin{array}{|c|c|c|c|} \hline x & 0 & 1 & 2 \\ \hline y & 1 & 3 & 9 \\ \hline \end{array}$$

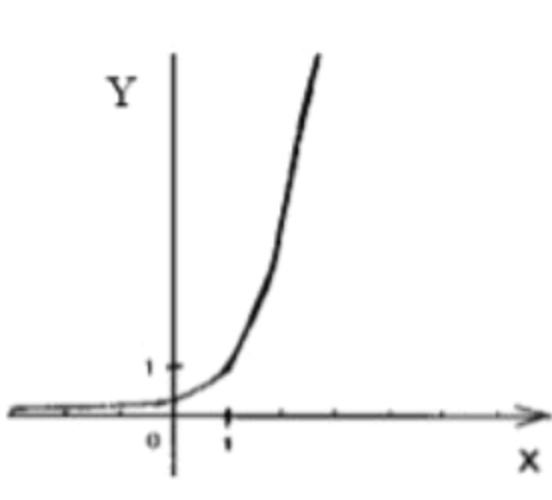
Построение графика функции $y = 3^x$:
График функции $y = 3^x$ представляет собой экспоненциальную кривую с теми же характеристиками, что и в предыдущем пункте.

Сдвиг графика вправо на 1 единицу:
У нас имеется функция $y = 3^{x-1}$, что означает сдвиг графика функции $y = 3^x$ на 1 единицу вправо по оси абсцисс.

Это происходит из-за изменения в экспоненциальной степени. Математически, сдвиг происходит за счет изменения $x-1$ вместо $x$, что смещает график вправо на 1 единицу. Если для $y = 3^x$ точка $(0, 1)$, то для $y = 3^{x-1}$ эта точка будет перемещена в $(1, 1)$.

3)
Уравнение:
$y = 2^{2-x} + 3 = \left( \frac{1}{2} \right)^{x-2} + 3$

Рассмотрим функцию $y = \left( \frac{1}{2} \right)^x$:

• Область определения: $x \in \mathbb{R}$.
• Множество значений: $y > 0$, так как $\left( \frac{1}{2} \right)^x$ всегда положительно.
• Монотонность: Функция убывает, так как основание степени $0 < \frac{1}{2} < 1$, следовательно, $\left( \frac{1}{2} \right)^x$ убывает с увеличением $x$.

Таблица значений функции $y = \left( \frac{1}{2} \right)^x$:

$$\begin{array}{|c|c|c|c|c|} \hline x & -3 & -2 & -1 & 0 \\ \hline y & 8 & 4 & 2 & 1 \\ \hline \end{array}$$

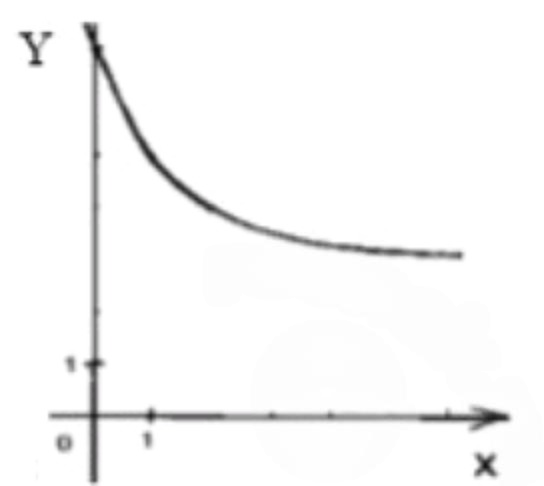
Построение графика функции $y = \left( \frac{1}{2} \right)^x$:
График функции $y = \left( \frac{1}{2} \right)^x$ представляет собой экспоненциальную кривую, которая убывает и приближается к оси абсцисс, но никогда её не пересекает (потому что значения всегда положительные).

Сдвиг графика вправо на 2 единицы и вверх на 3 единицы:
У нас имеется функция $y = \left( \frac{1}{2} \right)^{x-2} + 3$. Это означает два сдвига:

• Сдвиг вдоль оси абсцисс на 2 единицы вправо, так как аргумент функции изменен на $x — 2$ (перемещает график вправо).
• Сдвиг вдоль оси ординат на 3 единицы вверх, так как прибавляется 3 к функции $\left( \frac{1}{2} \right)^x$.

Таким образом, весь график функции $y = \left( \frac{1}{2} \right)^x$ будет сдвинут вправо на 2 единицы и вверх на 3 единицы. Если точка $(0, 1)$ принадлежала оригинальному графику, то теперь она будет находиться в точке $(2, 4)$.

Итог

Каждое из уравнений в задаче описывает сдвиг графика экспоненциальной функции. Сдвиг по оси абсцисс и ординат можно объяснить через изменения в аргументе функции и добавление/вычитание констант.