
Учебник «Алгебра» для 10-11 классов под авторством Алимова – это один из наиболее популярных и широко используемых учебных пособий для старшеклассников. Он заслужил признание как среди учителей, так и среди учеников благодаря своей структурированности, доступности изложения и качественной проработке материала.
ГДЗ по Алгебре 10-11 Класс Номер 237 Алимов — Подробные Ответы
- 2x = 3-2x-x2;
- 3^-x = корень x;
- (1/3)x=-3/x;
- (1/2)x= x3-1.
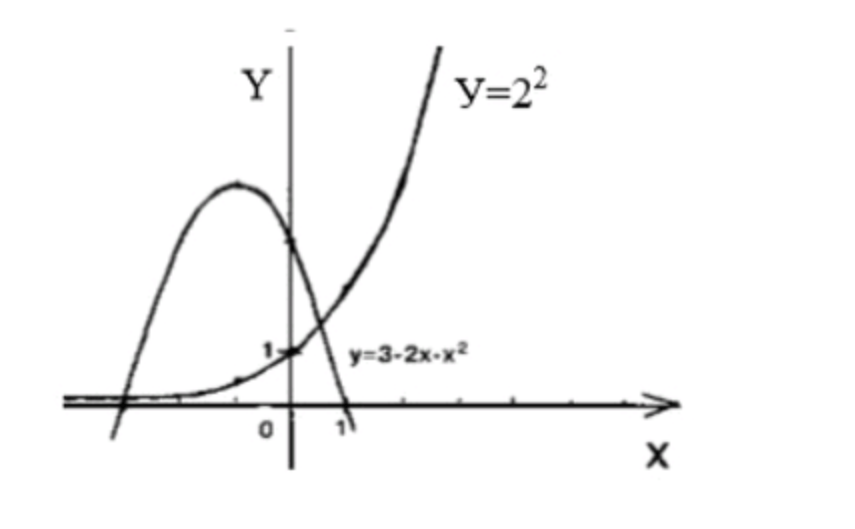
1)
2)
3)
4)
1)
Показательная функция:
- Рассмотрим функцию , которая является стандартной показательной функцией с основанием 2. Она всегда положительна и растет с увеличением . Для разных значений вычислим значения :
- ,
- ,
- ,
Получаем таблицу значений:
Парабола:
- Уравнение описывает параболу, которая открывается вниз. Находим вершину параболы с помощью формулы для абсциссы вершины , где , :
Теперь находим ординату вершины, подставив в уравнение параболы:
Получаем, что вершина параболы .
Таблица значений функции для нескольких значений :
Нахождение корней:
- Чтобы решить уравнение , приравниваем значения обеих функций:
- Сравнив графики функций, видим, что они пересекаются в двух точках:
Ответ: .
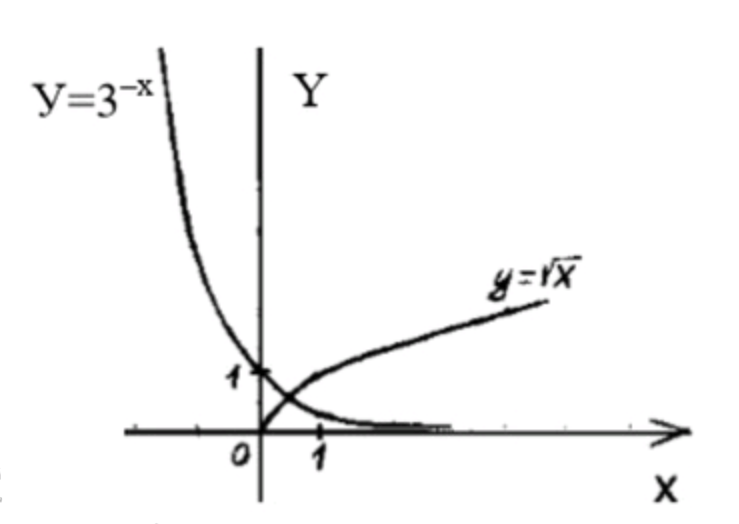
2)
Показательная функция:
- Рассмотрим функцию . Она является убывающей функцией. Для нескольких значений вычислим :
- ,
- ,
- ,
Таблица значений:
Функция :
- Уравнение описывает ветвь параболы, которая существует только для . Для нескольких значений :
- ,
- ,
- ,
- ,
Таблица значений:
Нахождение корня:
- Чтобы решить уравнение , приравниваем значения обеих функций:
- Сравнив графики функций, видим, что они пересекаются в одной точке:
Ответ: .
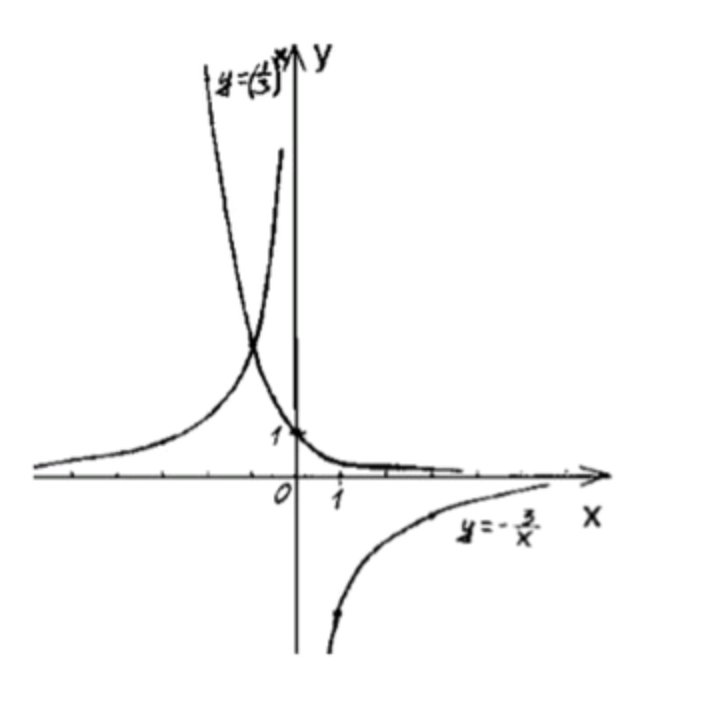
3)
Показательная функция:
- Рассмотрим функцию , которая является убывающей для . Для нескольких значений :
- ,
- ,
- ,
Таблица значений:
Гипербола:
- Уравнение описывает гиперболу. Для нескольких значений :
- ,
- ,
- ,
- ,
Таблица значений:
Нахождение корня:
- Чтобы решить уравнение , приравниваем значения обеих функций:
- Сравнив графики функций, видим, что они пересекаются в одной точке:
Ответ: .
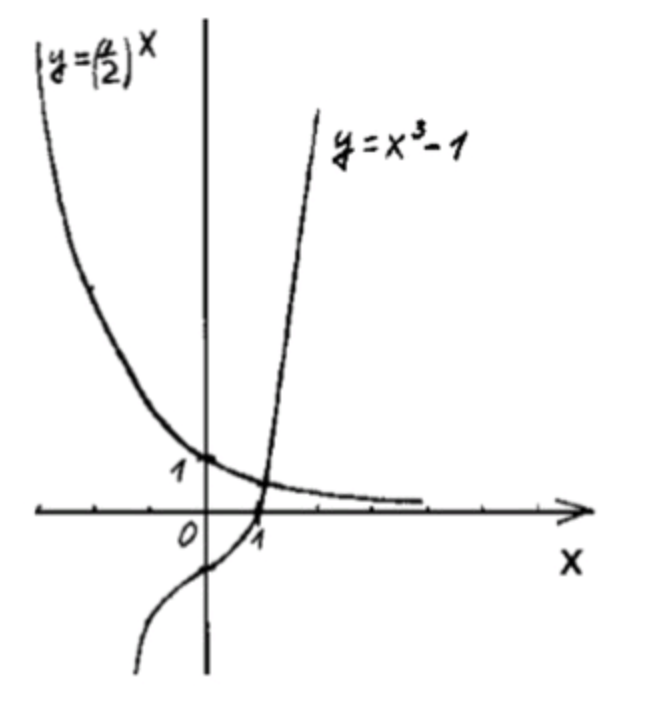
4)
Показательная функция:
- Рассмотрим функцию , которая является убывающей. Для нескольких значений :
- ,
- ,
- ,
- ,
Таблица значений:
Кубическая парабола:
- Уравнение описывает кубическую параболу. Для нескольких значений :
- ,
- ,
- ,
- ,
Таблица значений:
Нахождение корня:
- Чтобы решить уравнение , приравниваем значения обеих функций:
- Сравнив графики функций, видим, что они пересекаются в одной точке:
Ответ: .



Оставь свой отзыв 💬
Комментариев пока нет, будьте первым!