
Учебник «Алгебра» для 10-11 классов под авторством Алимова – это один из наиболее популярных и широко используемых учебных пособий для старшеклассников. Он заслужил признание как среди учителей, так и среди учеников благодаря своей структурированности, доступности изложения и качественной проработке материала.
ГДЗ по Алгебре 10-11 Класс Номер 205 Алимов — Подробные Ответы
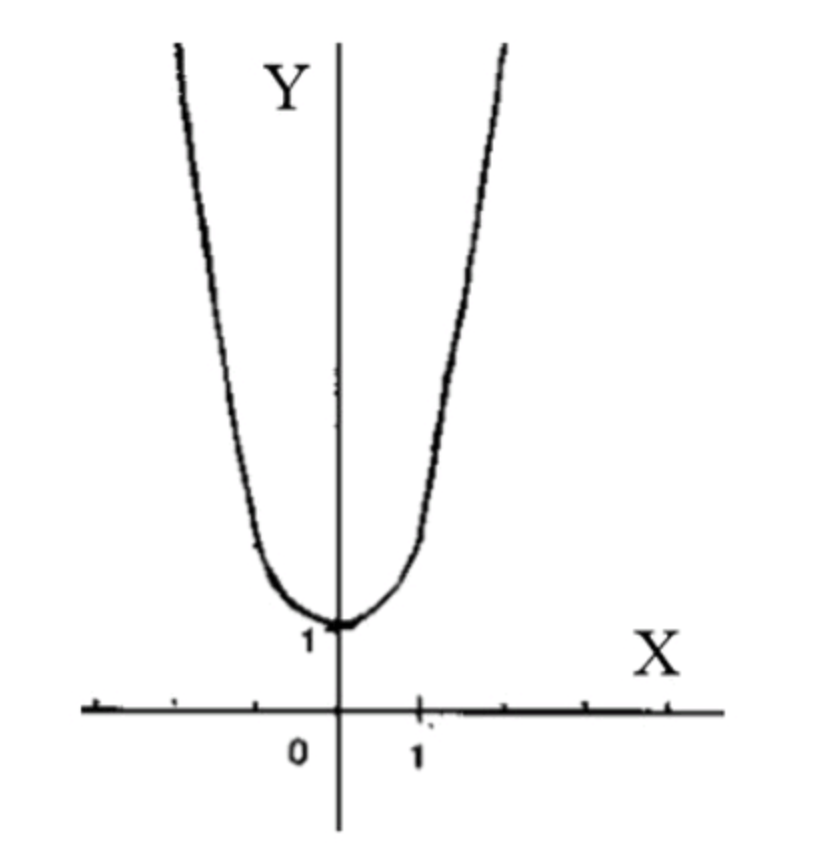
- y= 2^|x|;
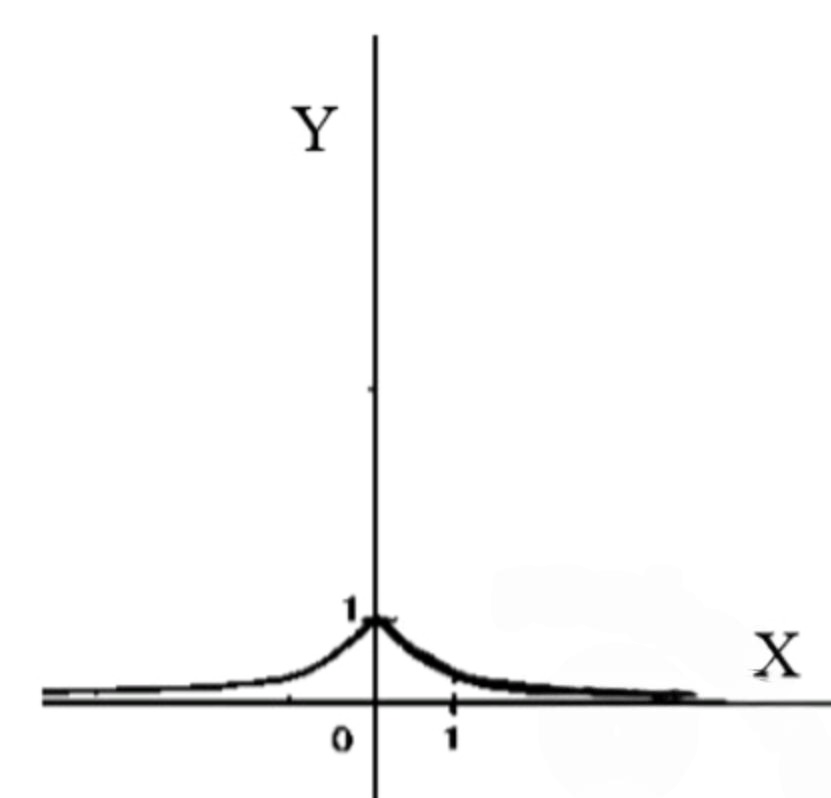
- y= (1/3)|x|;
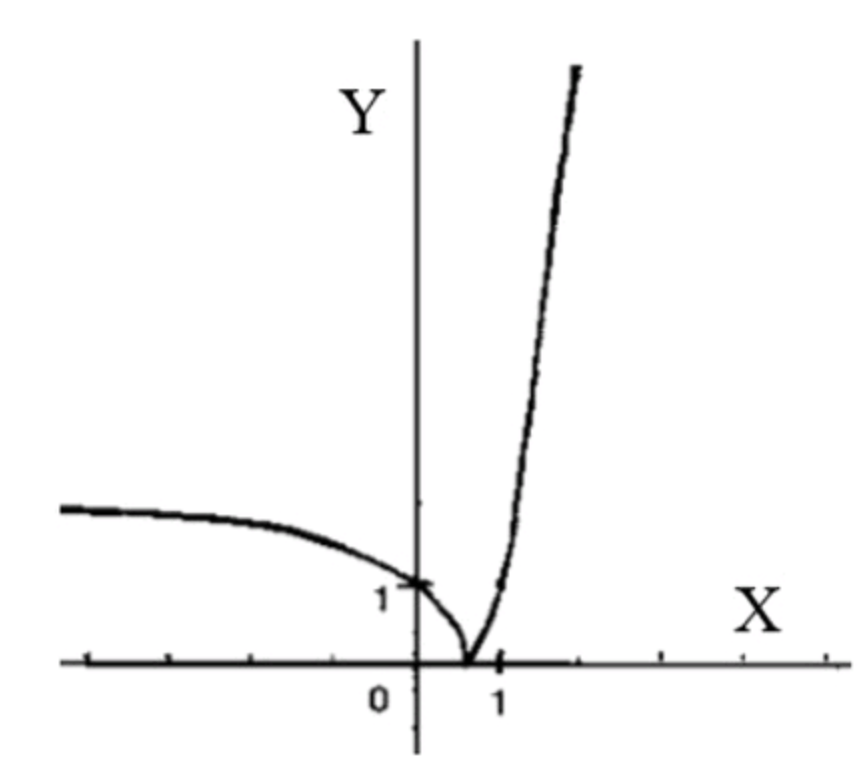
- y= |3x-2|;
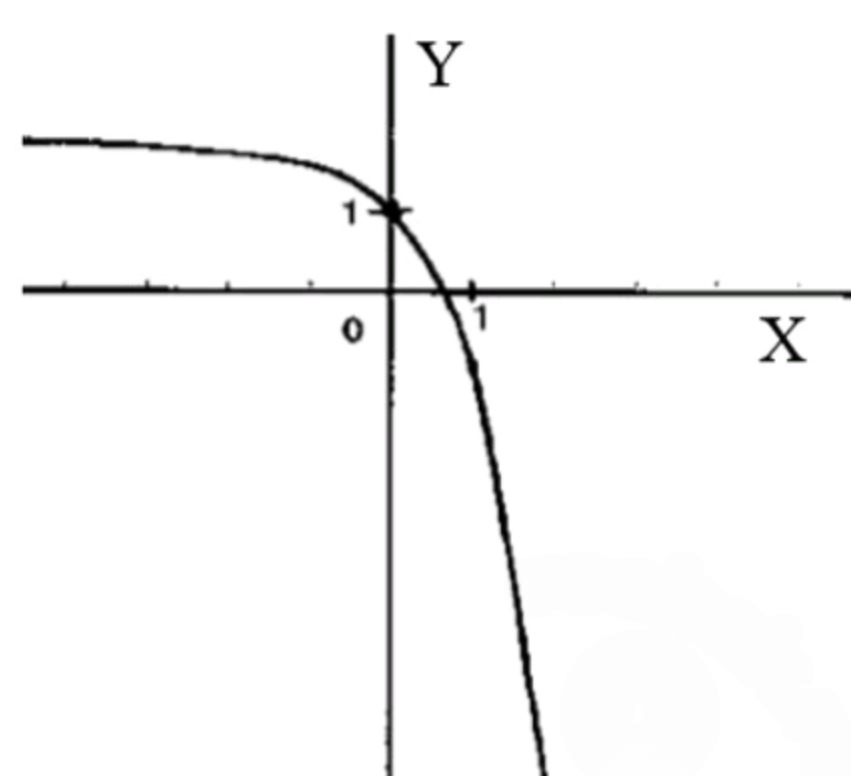
- y= 2-3x.
;
Функция является четной:
;
Если , тогда , значит:
- Область определения: ;
- Множество значений: ;
- Функция возрастает на и убывает на ;
Координаты некоторых точек:
График функции:
;
Функция является четной:
;
Если , тогда , значит:
- Область определения: ;
- Множество значений: ;
- Функция возрастает на и убывает на ;
Координаты некоторых точек:
График функции:
;
Рассмотрим функцию :
- Область определения: ;
- Множество значений: ;
- Функция возрастает, так как ;
Координаты некоторых точек:
Построим график функции и осуществим его сдвиг вдоль оси ординат на 2 единицы вниз, а затем отразим его часть, находящуюся под осью абсцисс:
;
Рассмотрим функцию :
- Область определения: ;
- Множество значений: ;
- Функция возрастает, так как ;
Координаты некоторых точек:
Построим график функции и отразим его относительно оси абсцисс, а затем осуществим его сдвиг вдоль оси ординат на 2 единицы вверх:
1.
Анализ функции
Рассмотрим функцию . Важно учитывать, что в этой функции присутствует абсолютное значение в показателе степени.
- Четность функции: Чтобы проверить, является ли функция четной, нужно доказать, что для всех .
- Рассмотрим . Поскольку , мы получаем, что , следовательно, функция является четной.
- Область определения: Функция экспоненциальная и определена для всех значений , так как существует для любых значений .
- Множество значений: Поскольку всегда больше или равно 1 для всех значений , то множество значений функции будет .
- Монотонность:
- При , функция возрастает, потому что основание степени 2 больше 1, и экспоненциальная функция всегда возрастает на .
- При , функция убывает, так как основание степени меньше 1, и такая функция убывает на .
Координаты некоторых точек: Рассмотрим несколько точек для функции:
При , . При , , и при , .
График функции:
- График будет симметричен относительно оси , так как функция четная.
- При график будет возрастать, а при — убывать.
- График функции выглядит как «половинка» экспоненциальной кривой, которая расширяется вверх и влево.
2.
Анализ функции
Рассмотрим функцию .
- Четность функции: Проверим, является ли функция четной:
Функция четная, так как .
- Область определения: Эта функция определена для всех значений , так как существует для всех .
- Множество значений: Поскольку всегда положительно и , то множество значений функции будет .
- Монотонность:
- При , функция убывает, так как основание меньше 1, и экспоненциальная функция убывает на .
- При , функция возрастает, поскольку увеличивается на .
Координаты некоторых точек:
При , . При , .
График функции:
- График функции будет симметричен относительно оси , так как функция четная.
- При график будет убывать, а при — возрастать.
- График будет похож на «половинку» экспоненциальной кривой, которая направлена вниз и влево.
3.
Анализ функции
Рассмотрим функцию .
- Область определения: Функция определена для всех , следовательно, функция также определена на всей числовой оси.
- Множество значений: Поскольку , функция всегда неотрицательна, и её множество значений будет .
- Монотонность:
- При , .
- При , , так что .
- При , , так что .
Координаты некоторых точек:
При , . При , . При , .
График функции:
- Сначала строим график функции .
- Затем сдвигаем его вдоль оси ординат на 2 единицы вниз.
- Отражаем часть графика, которая находится под осью абсцисс, относительно этой оси.
4.
Анализ функции
Рассмотрим функцию .
- Область определения: Функция определена для всех , следовательно, функция также определена на всей числовой оси.
- Множество значений: Поскольку всегда положительно, то всегда отрицательно для и может быть положительным для . Множество значений: .
- Монотонность: Функция убывает, так как возрастает.
Координаты некоторых точек:
При ,
. При , . При , .
График функции:
- Сначала строим график функции .
- Отражаем его относительно оси абсцисс.
- Затем сдвигаем его вдоль оси ординат на 2 единицы вверх.



Оставь свой отзыв 💬
Комментариев пока нет, будьте первым!