ГДЗ по Алгебре 10-11 Класс Учебник 📕 Алимов — Все Части

Алгебра

10-11 класс учебник Алимов

10 класс

Тип

ГДЗ, Решебник.

Автор

Ш.А. Алимов, Ю.М. Колягин, М.В. Ткачева.

Год

2015-2024.

Издательство

Просвещение.

Описание

Учебник «Алгебра» для 10-11 классов под авторством Алимова – это один из наиболее популярных и широко используемых учебных пособий для старшеклассников. Он заслужил признание как среди учителей, так и среди учеников благодаря своей структурированности, доступности изложения и качественной проработке материала.

Учебник охватывает весь необходимый курс алгебры для 10-11 классов, включая такие сложные темы, как производные, интегралы, логарифмы и элементы математического анализа. Материал представлен последовательно и логично, что позволяет ученикам постепенно углубляться в изучение предмета. Пособие включает как теоретическую часть, так и большое количество практических заданий различного уровня сложности, что способствует закреплению знаний.

Одной из главных особенностей учебника является наличие задач повышенной сложности, которые стимулируют развитие логического мышления и навыков решения нестандартных задач. Кроме того, в книге представлены примеры из реальной жизни, что делает изучение алгебры более интересным и прикладным.

Преимущества учебника

Четкая структура материала
Учебник разделен на главы и параграфы с последовательным изложением тем. Это позволяет ученикам легко ориентироваться в содержании и возвращаться к ранее изученным темам для повторения.
Пошаговые объяснения
Каждая новая тема сопровождается подробными примерами с пошаговым решением. Это помогает ученикам лучше понять алгоритмы выполнения задач.
Разнообразие упражнений
В учебнике представлены задачи разного уровня сложности: от базовых до олимпиадных. Это делает пособие полезным как для обычных школьников, так и для тех, кто готовится к экзаменам или олимпиадам.
Практическая направленность
Включение задач из реальной жизни (например, расчет процентов или использование математических моделей) помогает ученикам видеть практическое применение алгебры.
Подготовка к ЕГЭ
Учебник содержит задания, аналогичные тем, которые встречаются на ЕГЭ, что делает его отличным инструментом для подготовки к экзаменам.

Учебник «Алгебра» Алимова для 10-11 классов – это надежный помощник в изучении математики. Он подходит как для базового освоения предмета, так и для углубленного изучения. Благодаря четкой структуре, разнообразию заданий и ориентации на экзамены, данный учебник является одним из лучших выборов для старшеклассников.

ГДЗ по Алгебре 10-11 Класс Номер 201 Алимов — Подробные Ответы

Задача

Построить график функции:

y=3x-2;;
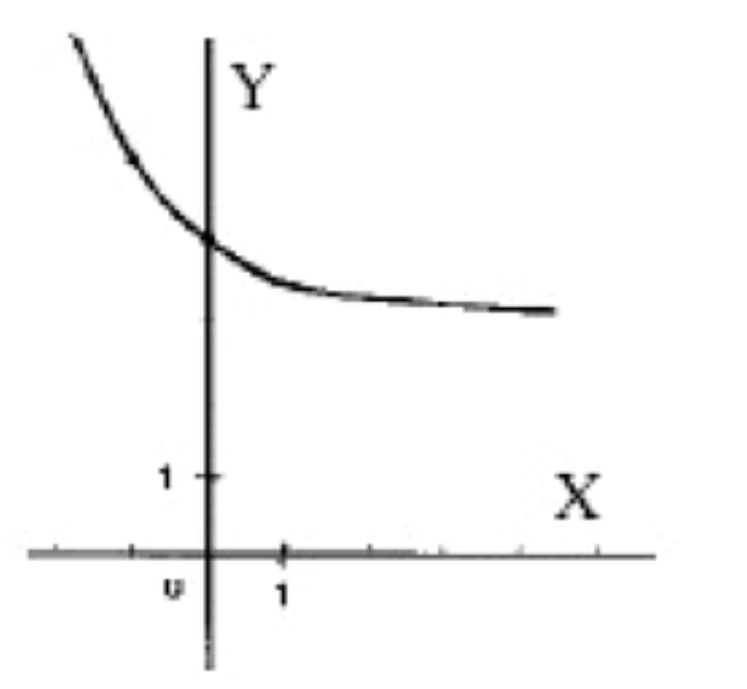
y=(1/2)x+3;
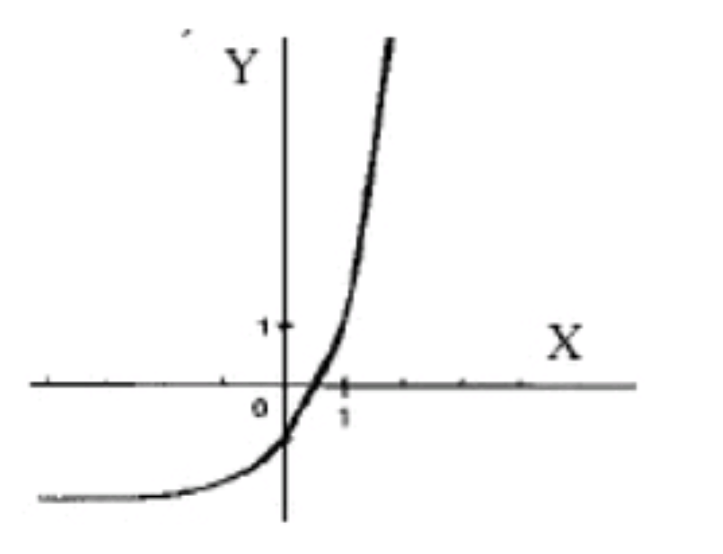
y=2^(x+1);
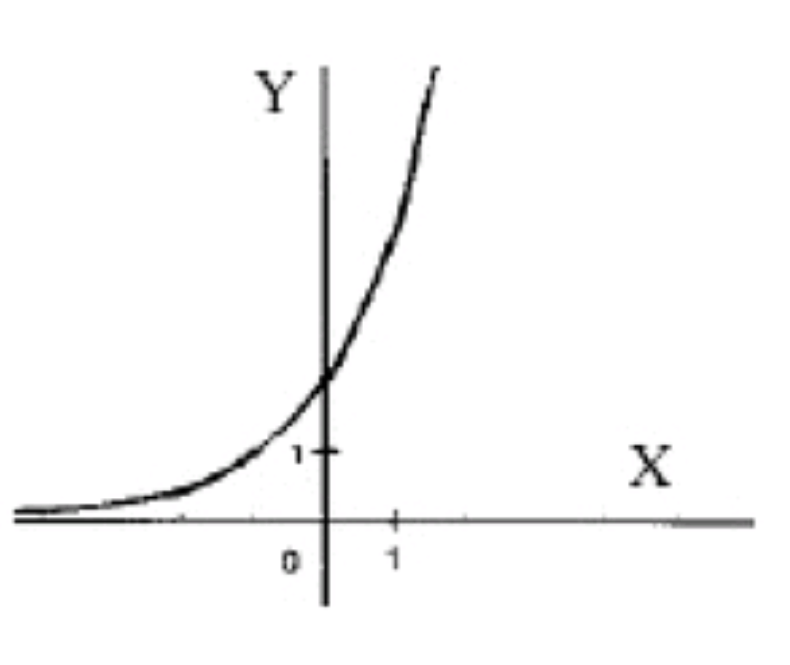
y=3^(x-2).

Краткий ответ:

1)

$y = 3^x — 2$

;

Рассмотрим функцию

$y = 3^x$

:

Область определения: $x \in \mathbb{R}$
;
Множество значений: $y > 0$
;
Функция возрастает, так как $3 > 1$
;

$x$	0	1	2
$y$	1	3	9

$x$

0

1

2

$y$

1

3

9

Построим график функции

$y = 3^x$

и осуществим его сдвиг вдоль оси ординат на 2 единицы вниз.

2)

$y = \left( \frac{1}{2} \right)^x + 3$

;

Рассмотрим функцию

$y = \left( \frac{1}{2} \right)^x$

:

Область определения: $x \in \mathbb{R}$
;
Множество значений: $y > 0$
;
Функция убывает, так как $0 < \frac{1}{2} < 1$
;

$x$	-3	-2	-1	0
$y$	11	7	5	4

$x$

-3

-2

-1

0

$y$

11

7

5

4

Построим график функции

$y = \left( \frac{1}{2} \right)^x$

и осуществим его сдвиг вдоль оси ординат на 3 единицы вверх.

3)

$y = 2^{x+1}$

;

Рассмотрим функцию

$y = 2^x$

:

Область определения: $x \in \mathbb{R}$
;
Множество значений: $y > 0$
;
Функция возрастает, так как $2 > 1$
;

$x$	0	1	2	3
$y$	1	2	4	8

$x$

0

1

2

3

$y$

1

2

4

8

Построим график функции

$y = 2^x$

и осуществим его сдвиг вдоль оси абсцисс на 1 единицу влево.

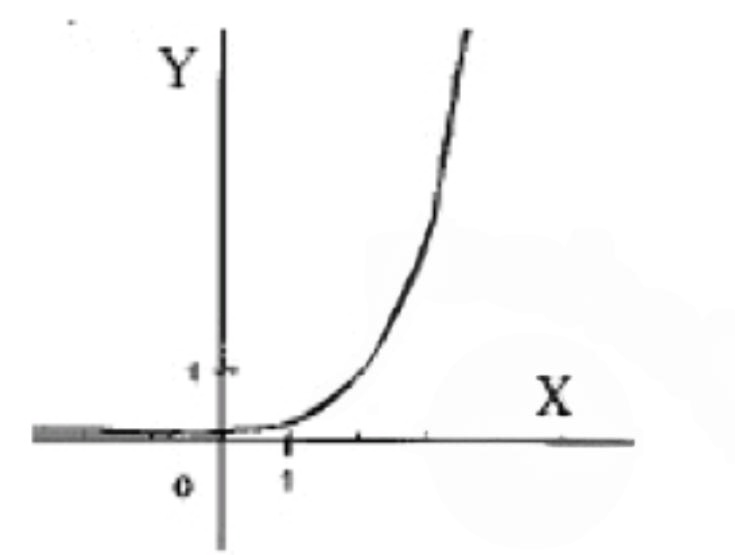
4)

$y = 3^{x-2}$

;

Рассмотрим функцию

$y = 3^x$

:

Область определения: $x \in \mathbb{R}$
;
Множество значений: $y > 0$
;
Функция возрастает, так как $3 > 1$
;

$x$	0	1	2
$y$	1	3	9

$x$

0

1

2

$y$

1

3

9

Построим график функции

$y = 3^x$

и осуществим его сдвиг вдоль оси абсцисс на 2 единицы вправо.

Подробный ответ:

1)

$y = 3^x — 2$

Шаг 1: Исходная функция

$y = 3^x$

Рассмотрим основную экспоненциальную функцию

$y = 3^x$

.

Область определения: $x \in \mathbb{R}$
(функция определена для всех действительных чисел).
Множество значений: $y > 0$
(значения функции всегда положительны, так как основание 3 больше 1).
Поведение функции: $y = 3^x$
— это возрастающая функция, так как основание 3 больше 1.

Построим таблицу значений:

$x$	0	1	2
$y$	1	3	9

$x$

0

1

2

$y$

1

3

9

Шаг 2: Сдвиг графика вниз на 2 единицы

Функция

$y = 3^x — 2$

получается из

$y = 3^x$

сдвигом вниз на 2 единицы.

Новая таблица значений:

$x$	0	1	2
$y$	-1	1	7

$x$

0

1

2

$y$

-1

1

7

График сместится вниз, и асимптота теперь будет находиться на уровне

$y = -2$

, вместо

$y = 0$

.

2)

$y = \left( \frac{1}{2} \right)^x + 3$

Шаг 1: Исходная функция

$y = \left( \frac{1}{2} \right)^x$

Рассмотрим основную экспоненциальную функцию

$y = \left( \frac{1}{2} \right)^x$

.

Область определения: $x \in \mathbb{R}$
(функция определена для всех действительных чисел).
Множество значений: $y > 0$
(значения функции всегда положительны).
Поведение функции: убывает, так как основание $\frac{1}{2}$
меньше 1.

Построим таблицу значений:

$x$	-3	-2	-1	0
$y$	8	4	2	1

$x$

-3

-2

-1

0

$y$

8

4

2

1

Шаг 2: Сдвиг графика вверх на 3 единицы

Функция

$y = \left( \frac{1}{2} \right)^x + 3$

получается сдвигом вверх на 3 единицы.

Новая таблица значений:

$x$	-3	-2	-1	0
$y$	11	7	5	4

$x$

-3

-2

-1

0

$y$

11

7

5

4

Горизонтальная асимптота теперь будет находиться на уровне

$y = 3$

, вместо

$y = 0$

.

3)

$y = 2^{x+1}$

Шаг 1: Исходная функция

$y = 2^x$

Рассмотрим основную экспоненциальную функцию

$y = 2^x$

.

Область определения: $x \in \mathbb{R}$
.
Множество значений: $y > 0$
.
Поведение функции: возрастает, так как основание 2 больше 1.

Построим таблицу значений:

$x$	0	1	2	3
$y$	1	2	4	8

$x$

0

1

2

3

$y$

1

2

4

8

Шаг 2: Сдвиг графика влево на 1 единицу

Функция

$y = 2^{x+1}$

получается сдвигом графика

$y = 2^x$

на 1 единицу влево.

Новая таблица значений:

$x$	-1	0	1	2
$y$	1	2	4	8

$x$

-1

0

1

2

$y$

1

2

4

8

График остается возрастающим, а горизонтальная асимптота остается на уровне

$y = 0$

.

4)

$y = 3^{x-2}$

Шаг 1: Исходная функция

$y = 3^x$

Рассмотрим основную экспоненциальную функцию

$y = 3^x$

.

Область определения: $x \in \mathbb{R}$
.
Множество значений: $y > 0$
.
Поведение функции: возрастает, так как основание 3 больше 1.

Построим таблицу значений:

$x$	0	1	2
$y$	1	3	9

$x$

0

1

2

$y$

1

3

9

Шаг 2: Сдвиг графика вправо на 2 единицы

Функция

$y = 3^{x-2}$

получается сдвигом графика

$y = 3^x$

на 2 единицы вправо.

Новая таблица значений:

$x$	2	3	4
$y$	1	3	9

$x$

2

3

4

$y$

1

3

9

График остается возрастающим, а горизонтальная асимптота остается на уровне

$y = 0$

.

Вывод

Каждая из данных функций является экспоненциальной и получается из базовой функции

$y = a^x$

с помощью сдвигов вдоль осей координат.

Добавление или вычитание константы ( $\pm C$
) влияет на вертикальное положение графика.
Изменение переменной внутри показателя ( $x \pm C$
) влияет на горизонтальное положение графика.
Основание экспоненты больше 1 (рост) или между 0 и 1 (убывание) определяет характер изменения функции.

Оцени решение

← Предыдущий Следующий →

Сообщить об ошибке

Алгебра