ГДЗ по Алгебре 10-11 Класс Номер 194 Алимов — Подробные Ответы

Изобразить схематически график функции:

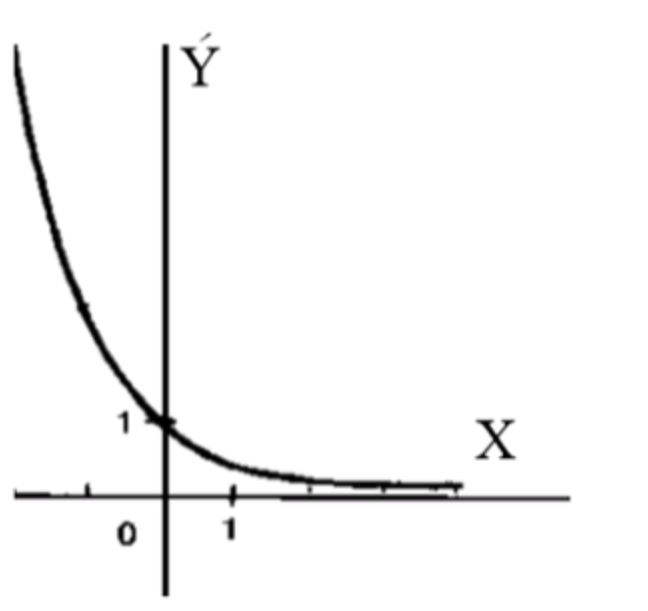
1. y= 0,4x;
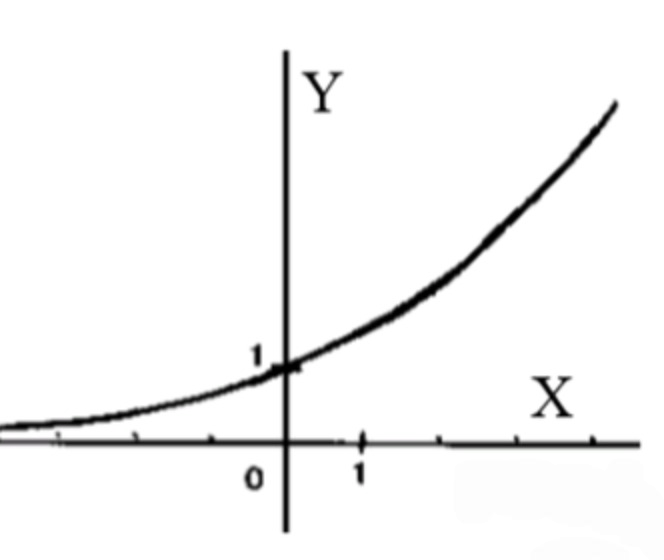
2. y= (корень 2)x;
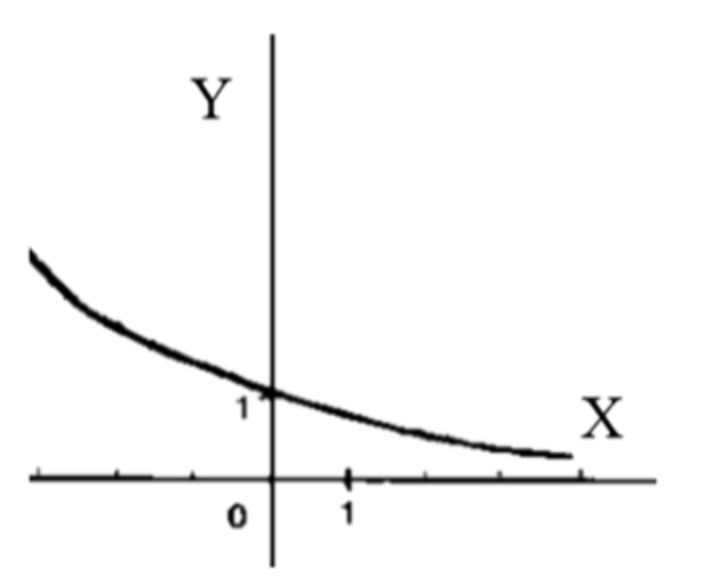
3. y=(1/корень 2)x;
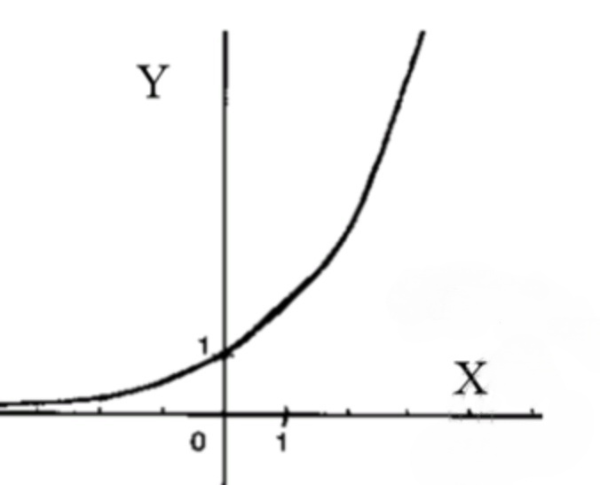
4. y=(корень 3)x.

1)$$y = 0.4^x;$$

• Область определения: $x\in \mathbb{R;}$
• Множество значений: $y>0$;
• Функция убывает, так как $0.4<1$;

Схематический график функции:

2)$$y = (\sqrt{2})^x;$$

• Область определения: $x\in \mathbb{R}$;
• Множество значений: $y>0$;
• Функция возрастает:

$$2 > 1 \quad => \quad \sqrt{2} > 1;$$

Схематический график функции:

3)$$y = \left(\frac{1}{\sqrt{2}}\right)^x;$$

• Область определения: $x\in \mathbb{R}$$$;
• Множество значений: $y>0$$$;
• Функция убывает:

$$2 > 1 \quad => \quad \sqrt{2} > 1 \quad => \quad \frac{1}{\sqrt{2}} < 1;$$

Схематический график функции:

4)$$y = (\sqrt{3})^x;$$

• Область определения: $x\in \mathbb{R}$$$;
• Множество значений: $y>0$;
• Функция возрастает:

$$3 > 1 \quad => \quad \sqrt{3} > 1;$$

Схематический график функции:

1. Функция $y = 0.4^x$

1.1. Определение функции

Функция имеет показательный вид:

$$y = 0.4^x$$

Здесь:

• $0.4$ — основание степени (меньше 1);
• $x$ — показатель степени (переменная).

1.2. Область определения

Показательная функция всегда определена для всех значений $x$, так как возведение любого положительного числа (0.4) в любую степень даёт корректное значение.

$$x \in \mathbb{R}$$

1.3. Множество значений

Функция принимает только положительные значения, так как:

• $0.4^x$ всегда больше 0, независимо от $x$;
• Даже при больших отрицательных x, степень даёт дробное число, но остаётся положительной.

Таким образом:

$$y > 0$$

1.4. Поведение функции

Функция убывает, так как основание $0.4$ меньше 1. Это означает, что:

• При увеличении x значение $y$ уменьшается.
• При уменьшении x значение $y$ увеличивается.

1.5. График функции

График показательной функции $y = 0.4^x$ убывает и приближается к оси $x$, но никогда её не пересекает.

2. Функция $y = (\sqrt{2})^x$

2.1. Определение функции

Функция задана как:

$$y = (\sqrt{2})^x$$

Здесь:

$\sqrt{2} \approx 1.414$ — основание степени (больше 1).

2.2. Область определения

Функция определена для всех значений $x$:

$$x \in \mathbb{R}$$

2.3. Множество значений

Поскольку $(\sqrt{2})^x$ всегда положительно для любых $x$, то:

$$y > 0$$

2.4. Поведение функции

Функция возрастает, так как основание $\sqrt{2}$больше 1. Это значит, что:

• При увеличении x значение $y$ увеличивается.
• При уменьшении x значение $y$ уменьшается, но остаётся положительным.

2.5. График функции

График показательной функции $y = (\sqrt{2})^x$ растёт и стремится к бесконечности при увеличении $x$.

3. Функция $y = \left(\frac{1}{\sqrt{2}}\right)^x$

3.1. Определение функции

Функция задана как:

$$y = \left(\frac{1}{\sqrt{2}}\right)^x$$

Здесь:

$\frac{1}{\sqrt{2}} = \sqrt{2}^{-1} \approx 0.707$, что меньше 1.

3.2. Область определения

Функция определена для всех значений $x$:

$$x \in \mathbb{R}$$

3.3. Множество значений

Так как $\left(\frac{1}{\sqrt{2}}\right)^x$всегда положительно, то:

$$y > 0$$

3.4. Поведение функции

Функция убывает, так как основание меньше 1. Это значит, что:

• При увеличении x значение $y$ уменьшается.
• При уменьшении x значение $y$ увеличивается.

3.5. График функции

График функции $y = \left(\frac{1}{\sqrt{2}}\right)^x$убывает и стремится к нулю при увеличении $x$.

4. Функция $y = (\sqrt{3})^x$

4.1. Определение функции

Функция задана как:

$$y = (\sqrt{3})^x$$

Здесь:

$\sqrt{3} \approx 1.732$, что больше 1.

4.2. Область определения

Функция определена для всех значений $x$:

$$x \in \mathbb{R}$$

4.3. Множество значений

Поскольку $(\sqrt{3})^x$ всегда положительно для любых $x$, то:

$$y > 0$$

4.4. Поведение функции

Функция возрастает, так как основание $\sqrt{3}$больше 1. Это значит, что:

• При увеличении x значение $y$ увеличивается.
• При уменьшении x значение $y$ уменьшается, но остаётся положительным.

4.5. График функции

График показательной функции $y = (\sqrt{3})^x$ растёт и стремится к бесконечности при увеличении $x$.