ГДЗ по Алгебре 10-11 Класс Номер 184 Алимов — Подробные Ответы

Изобразить схематически на одном рисунке графики функций:

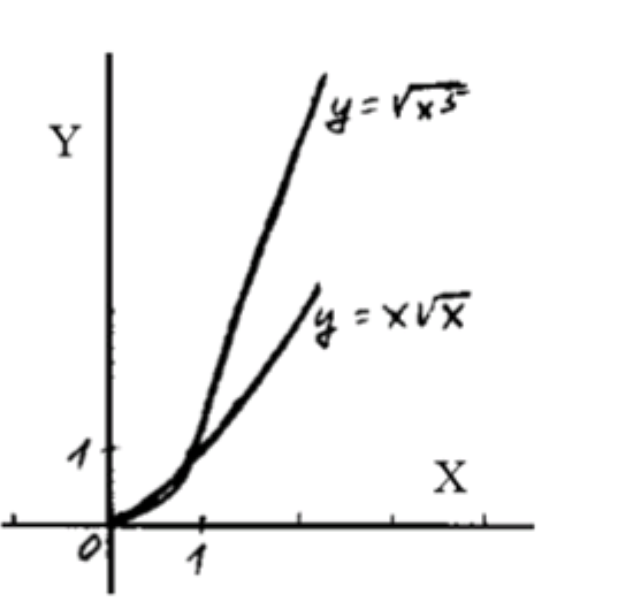
1. y= корень x5,y=x корень x;
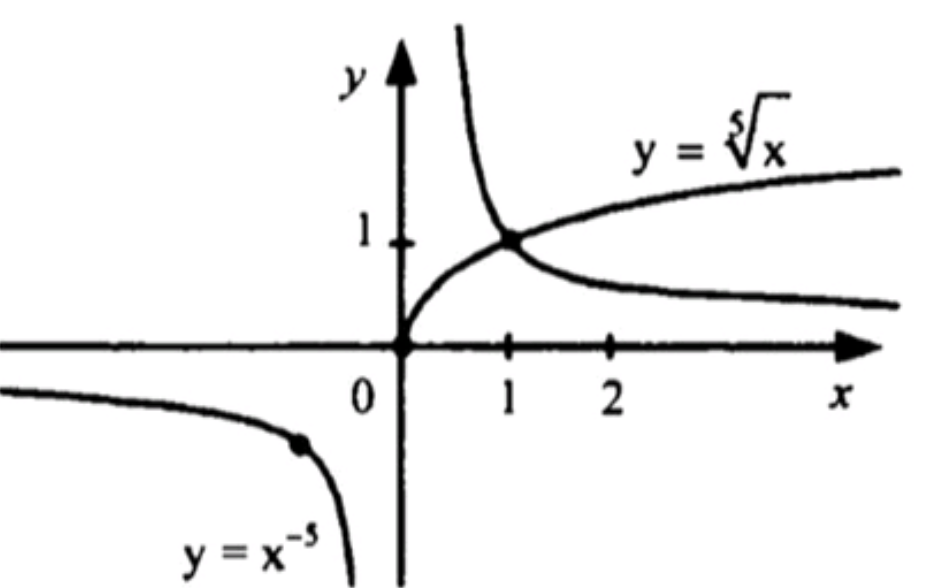
2. y= корень 5 степени x, y=x^-5.

1) $y = \sqrt{x^5}$и $y = x\sqrt{x}$;

Функция $y = \sqrt{x^5} = x^{\frac{5}{2}}$:

• Область определения: $x\ge 0$;
• Множество значений: $y\ge 0$;
• Функция возрастает;

Функция $y = x\sqrt{x} = x^{\frac{3}{2}}$:

• Область определения: $x\ge 0$;
• Множество значений: $y\ge 0$;
• Функция возрастает;

Схематические графики функций:

2) $y = \sqrt[5]{x}$и $y = x^{-5}$;

Функция$y = \sqrt[5]{x} = x^{\frac{1}{5}}$:

• Область определения: $x\ge 0$;
• Множество значений: $y\ge 0$;
• Функция возрастает;

Функция $y = x^{-5}$:

• Область определения: $x\mathrm{\ne }0$;
• Множество значений: $y\mathrm{\ne }0$;
• Функция убывает;
• Функция является нечетной;

Схематические графики функций:

1) Функция $y = \sqrt{x^5}$ и $y = x\sqrt{x}$

Функция $y = \sqrt{x^5} = x^{\frac{5}{2}}$:

• Область определения: Функция $y=\sqrt{x^5}$представлена как $x^{\frac{5}{2}}$, и для вычисления этой функции важно, чтобы подкоренное выражение $x^5$ было неотрицательным. Так как для всех $x \geq 0$ выражение $x^5$ всегда положительно, функция будет определена при всех значениях $x \geq 0$.

$$\text{Область определения: } x \geq 0.$$

• Множество значений: Так как $x^{\frac{5}{2}}$ принимает только неотрицательные значения для $x\ge 0$, то множество значений функции будет включать все значения $y \geq 0$.

$$\text{Множество значений: } y \geq 0.$$

• Анализ функции: Поскольку степень $\frac{5}{2}$ больше нуля, функция будет возрастать. Для всех $x\ge 0$, когда значение $x$

$$\text{Функция возрастает для } x \geq 0.$$

Функция $y = x\sqrt{x} = x^{\frac{3}{2}}$:

Область определения: Функция $y=x\sqrt{x}$имеет вид $x^{\frac{3}{2}}$, и для вычисления этой функции подкоренное выражение $x$ также должно быть неотрицательным. Таким образом, функция будет определена для всех значений $x \geq 0$.

$$\text{Область определения: } x \geq 0.$$

• Множество значений: Аналогично предыдущей функции, функция $y=x^{\frac{3}{2}}$ принимает только неотрицательные значения для $x\ge 0$, и множество значений функции будет включать все значения $y \geq 0$.

$$\text{Множество значений: } y \geq 0.$$

• Анализ функции: Поскольку степень $\frac{3}{2}$ больше нуля, функция будет возрастать. Для всех $x\ge 0$, когда значение $x$

$$\text{Функция возрастает для }x\ge 0.$$

$$\text{Функция возрастает для } x \geq 0.$$2) Функция $y = \sqrt[5]{x}$и $y = x^{-5}$

Функция $y = \sqrt[5]{x} = x^{\frac{1}{5}}$:

• Область определения: Функция $y=\sqrt[5]{x}$представляет собой пятую степень корня из $x$, который определён для всех действительных $x$, так как корень пятой степени можно извлечь из любого действительного числа. Следовательно, область определения функции $y = \sqrt[5]{x}$будет $x \in \mathbb{R}$.

$$\text{Область определения: } x \in \mathbb{R}.$$

• Множество значений: Функция $y=x^{\frac{1}{5}}$ принимает все действительные значения, так как корень пятой степени из любого действительного числа может быть как положительным, так и отрицательным, включая ноль.
  $y = x^{\frac{1}{5}}$

$$\text{Множество значений: } y \in \mathbb{R}.$$

• Анализ функции: Поскольку степень $\frac{1}{5}$ положительна, функция будет возрастать, то есть для $x>0$ функция возрастает, а для $x<0$ — тоже возрастает, но принимает отрицательные значения.
  $\frac{1}{5}$$x > 0$

$$\text{Функция возрастает для всех } x \in \mathbb{R}.$$

Функция $y = x^{-5}$:

• Область определения: Функция $y=x^{-5}$ имеет вид $y=\frac{1}{x^5}$. Эта функция определена для всех значений $x\mathrm{\ne }0$, так как при $x=0$ выражение $x^{-5}$ становится неопределённым.
  $y = x^{-5}$$x^{-5}$

$$\text{Область определения: } x \neq 0.$$

• Множество значений: Для $x>0$ функция $y=x^{-5}$ принимает положительные значения, а для $x<0$ функция $y=x^{-5}$ будет отрицательной, так как степень $-\mathrm{5\; нечетная.\; Следовательно,\; множество\; значений}$$\mathrm{}$$\mathrm{<math\; xmlns="http://www.w3.org/1998/Math/MathML"><semantics><mrow><mi> y\; не\; включает\; ноль.</mi></mrow></semantics></math>}$$y$

$$\text{Множество значений: } y \neq 0.$$

• Анализ функции: Функция $y=x^{-5}$ является убывающей. Для $x>0$, когда $x$ увеличивается, значение функции уменьшается. Для $x < 0$ значение функции также уменьшается, но остаётся отрицательным.

$$\text{Функция убывает для } x \neq 0.$$

• Нечетность функции: Функция $y=x^{-5}$ является нечетной, так как выполняется следующее условие:
  $y = x^{-5}$

$$f(-x) = (-x)^{-5} = -x^{-5} = -f(x).$$

Следовательно, функция является нечетной.

$$\text{Функция является нечетной}.$$