ГДЗ по Алгебре 10-11 Класс Номер 178 Алимов — Подробные Ответы

Решить уравнение с помощью графиков:

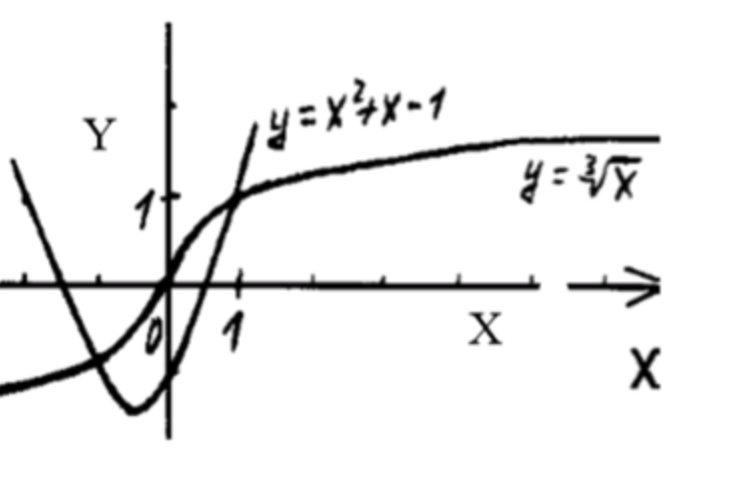
1. корень 3 степени x = x2+x-1;
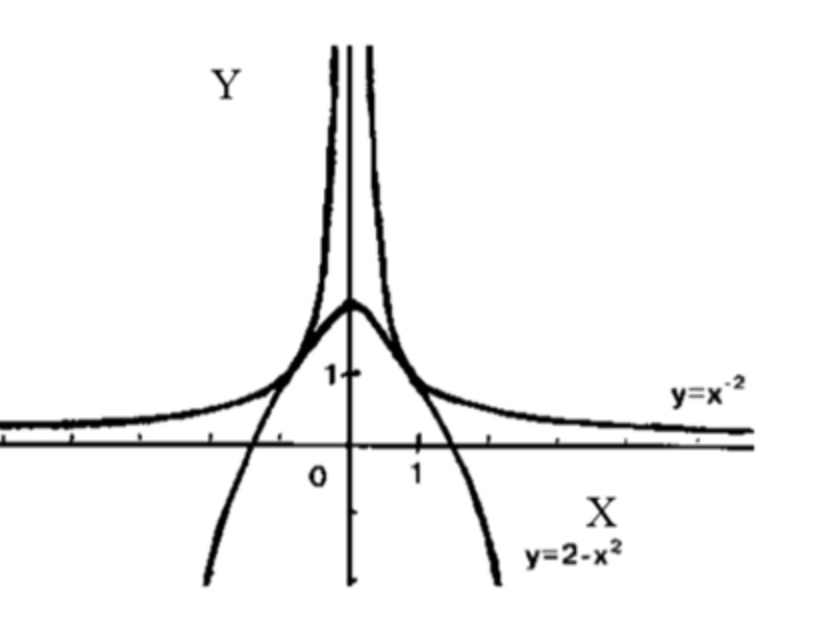
2. x^-2 = 2-x2.

1). $\sqrt[3]{x} = x^2 + x — 1$;

$y = \sqrt[3]{x}$— уравнение кубической параболы:

$$\begin{array}{|c|c|c|c|c|c|} \hline x & -8 & -1 & 0 & 1 & 8 \\ \hline y & -2 & -1 & 0 & 1 & 2 \\ \hline \end{array}$$

$y = x^2 + x — 1$ — уравнение параболы:

$x_0 = -\frac{b}{2a} = -\frac{1}{2}$ и $y_0 = \frac{1}{4} — \frac{1}{2} — 1 = -1\frac{1}{4}$;

$$\begin{array}{|c|c|c|c|c|c|c|} \hline x & -3 & -2 & -1 & 0 & 1 & 2 \\ \hline y & 5 & 1 & -1 & -1 & 1 & 5 \\ \hline \end{array}$$

Графики функций:

Ответ: $x = \pm 1$

$x^{-2} = 2 — x^2$;

$y = x^{-2}$ — уравнение гиперболы:

$x \neq 0$ и $y > 0$;

Возрастает при $x < 0$ и убывает при $x > 0$;

$$\begin{array}{|c|c|c|} \hline x & -1 & 1 \\ \hline y & 1 & 1 \\ \hline \end{array}$$

$y = 2 — x^2$ — уравнение параболы:

$x_0 = 0$ и $y_0 = 2 — 0^2 = 2$;

$$\begin{array}{|c|c|c|c|c|c|c|} \hline x & -3 & -2 & -1 & 1 & 2 & 3 \\ \hline y & -7 & -2 & 1 & 1 & -2 & -7 \\ \hline \end{array}$$

Графики функций:

Ответ: $x=\pm 1$

1) Уравнение $\sqrt[3]{x} = x^2 + x — 1$

Шаг 1: График функции $y = \sqrt[3]{x}$

Функция $y = \sqrt[3]{x}$— это кубический корень от $x$, который представляет собой уравнение кубической параболы. Рассмотрим значения функции для нескольких $x$:

Мы видим, что при $x = -8$, $x = -1$, $x = 0$, $x = 1$ и $x = 8$ соответствующие значения функции $y$ равны $-2$, $-1$, $0$, $1$, и $2$ соответственно. Это дает нам несколько точек на графике кубической функции $y = \sqrt[3]{x}$.

Шаг 2: График функции $y = x^2 + x — 1$

Теперь рассмотрим параболу $y = x^2 + x — 1$. Эта функция — стандартное уравнение параболы, и ее вершина находится по формуле:

$$x_0 = -\frac{b}{2a} = -\frac{1}{2} \quad \text{(где \( a = 1 \), \( b = 1 \))}$$

Теперь находим значение $y_0$ в вершине:

$$y_0 = x_0^2 + x_0 — 1 = \left(-\frac{1}{2}\right)^2 + \left(-\frac{1}{2}\right) — 1 = \frac{1}{4} — \frac{1}{2} — 1 = -\frac{5}{4} \approx -1.25$$

Рассмотрим несколько значений функции $y = x^2 + x — 1$ для различных значений $x$:

Шаг 3: Сравнение графиков

График функции $y=\sqrt[3]{x}$будет гладким, проходящим через начало координат, и будет увеличиваться с ростом $x$, как для положительных, так и для отрицательных значений $x$.

График функции $y=x^2+x-1$— это парабола, открытая вверх, с вершиной в точке $\left(-\frac{1}{2}, -\frac{5}{4}\right)$.

Шаг 4: Решение уравнения

Необходимо решить уравнение $\sqrt[3]{x} = x^2 + x — 1$. Поставим на графиках обе функции и найдем точки пересечения.

Мы видим, что обе функции пересекаются в точках $x=\pm 1$.

Ответ: $x = \pm 1$

2) Уравнение $x^{-2} = 2 — x^2$

Шаг 1: График функции $y = x^{-2}$

Функция $y = x^{-2}$ — это гипербола, которая существует только для $x \neq 0$ и всегда положительна ($y > 0$).

Для $x<0$ функция возрастает, а для $x>0$ — убывает.

Рассмотрим несколько значений для $x^{-2}$:

Шаг 2: График функции $y = 2 — x^2$

Теперь рассмотрим параболу $y = 2 — x^2$, которая имеет вершину в точке $x_0 = 0$, где $y_0 = 2$. Рассмотрим несколько значений для этой функции:

Шаг 3: Сравнение графиков

• График функции $y=x^{-2}$ будет гиперболой, которая стремится к бесконечности при $x\to 0$ и уменьшается при увеличении $\mathrm{\mid }x\mathrm{\mid }$.
• График функции $y=2-x^2$ — это парабола, открытая вниз, с вершиной в точке $(0,2)$.

Шаг 4: Решение уравнения

Необходимо решить уравнение $x^{-2} = 2 — x^2$. Поставим обе функции на графики и найдем точки пересечения.

Мы видим, что они пересекаются в точках $x=\pm 1$.

Ответ: $x = \pm 1$