ГДЗ по Алгебре 10-11 Класс Номер 176 Алимов — Подробные Ответы

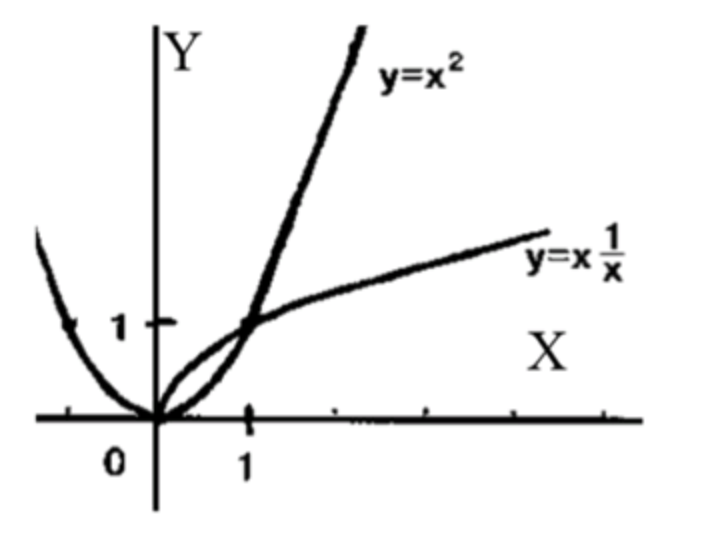
На одном рисунке построить графики функций у = х2 и y =x^корень x. Сравнить значения этих функций при х, равном 0; 0,5; 1; 3/2;2;3; 4; 5.

Построить графики функций:

$y = x^2$

и

$y = x^{\sqrt{x}}$

;

1)

$y = x^2$

— уравнение параболы:

2)

$y = x^{\sqrt{x}}$

— показательно-степенная функция:

3) Графики функций:

4) Сравним значения функций:

• При
  $x = 0$ 

  : $x^{\sqrt{x}} > x^2$ 

  ;

• При
  $x = 0.5$ 

  : $x^{\sqrt{x}} > x^2$ 

  ;

• При
  $x = 1$ 

  : $x^{\sqrt{x}} = x^2$ 

  ;

• При
  $x = \frac{3}{2}$ 

  : $x^{\sqrt{x}} < x^2$ 

  ;

• При
  $x = 2$ 

  : $x^{\sqrt{x}} < x^2$ 

  ;

• При
  $x = 3$ 

  : $x^{\sqrt{x}} < x^2$ 

  ;

• При
  $x = 4$ 

  : $x^{\sqrt{x}} = x^2$ 

  ;

• При
  $x = 5$ 

  : $x^{\sqrt{x}} > x^2$ 

  ;

Построить графики функций:

$y = x^2$

и

$y = x^{\sqrt{x}}$

;

1)

$y = x^2$

— уравнение параболы:

Функция

$y = x^2$

— это стандартное уравнение параболы, которая открывается вверх. Парабола симметрична относительно оси

$y$

, то есть для каждого значения

$x$

, его отрицательная версия даёт такое же значение

$y$

.

Для разных значений

$x$

вычислим значения функции:

График этой функции представляет собой параболу, которая проходит через точку

$(0, 0)$

и симметрична относительно оси

$y$

. Значения функции увеличиваются, когда

$x$

отдаляется от нуля в любую сторону.

2)

$y = x^{\sqrt{x}}$

— показательно-степенная функция:

Для функции

$y = x^{\sqrt{x}}$

, где показатель степени является корнем, видим, что значения функции сильно зависят от значений

$x$

. Эта функция является показательно-степенной, где показатель степени

$\sqrt{x}$

увеличивается по мере роста

$x$

, но сама функция имеет интересные особенности, когда

$x$

стремится к нулю и когда

$x$

становится большим.

Для разных значений

$x$

, вычислим значения функции:

• При
  $x = 0$ 

  , $y = 1$ 

  , так как $0^{\sqrt{0}} = 1$ 

  .

• При
  $x = 0.1$ 

  , $y \approx 0.5$ 

  .

• При
  $x = 0.5$ 

  , $y \approx 0.6$ 

  .

• При
  $x = 1$ 

  , $y = 1$ 

  , так как $1^{\sqrt{1}} = 1$ 

  .

• При
  $x = 2$ 

  , $y \approx 2.7$ 

  .

• При
  $x = 3$ 

  , $y \approx 6.7$ 

  .

• При
  $x = 4$ 

  , $y = 16$ 

  .

• При
  $x = 5$ 

  , $y \approx 36.5$ 

  .

График этой функции имеет экспоненциальный рост, при этом функция увеличивается с увеличением

$x$

, но на начальных этапах, например, при малых

$x$

, рост происходит не так быстро.

3) Графики функций:

4) Сравним значения функций:

Теперь, сравнив значения обеих функций при различных

$x$

, мы можем определить, как функции ведут себя друг относительно друга:

• При
  $x = 0$ 

  : $x^{\sqrt{x}} = 1$ 

  , $x^2 = 0$ 

  . Следовательно, $x^{\sqrt{x}} > x^2$ 

  .

• При
  $x = 0.5$ 

  : $x^{\sqrt{x}} \approx 0.6$ 

  , $x^2 = 0.25$ 

  . Следовательно, $x^{\sqrt{x}} > x^2$ 

  .

• При
  $x = 1$ 

  : $x^{\sqrt{x}} = 1$ 

  , $x^2 = 1$ 

  . Следовательно, $x^{\sqrt{x}} = x^2$ 

  .

• При
  $x = \frac{3}{2}$ 

  : $x^{\sqrt{x}} \approx 1.837$ 

  , $x^2 = 2.25$ 

  . Следовательно, $x^{\sqrt{x}} < x^2$ 

  .

• При
  $x = 2$ 

  : $x^{\sqrt{x}} \approx 2.7$ 

  , $x^2 = 4$ 

  . Следовательно, $x^{\sqrt{x}} < x^2$ 

  .

• При
  $x = 3$ 

  : $x^{\sqrt{x}} \approx 6.7$ 

  , $x^2 = 9$ 

  . Следовательно, $x^{\sqrt{x}} < x^2$ 

  .

• При
  $x = 4$ 

  : $x^{\sqrt{x}} = 16$ 

  , $x^2 = 16$ 

  . Следовательно, $x^{\sqrt{x}} = x^2$ 

  .

• При
  $x = 5$ 

  : $x^{\sqrt{x}} \approx 36.5$ 

  , $x^2 = 25$ 

  . Следовательно, $x^{\sqrt{x}} > x^2$ 

  .

Таким образом, можно сделать выводы о поведении этих двух функций для различных значений

$x$

:

• Для малых значений
  $x$ 

  , особенно при $x \in [0, 1]$ 

  , функция $x^{\sqrt{x}}$ 

  больше или равна функции $x^2$ 

  .

• Для
  $x > 1$ 

  , функция $x^2$ 

  начинает расти быстрее, чем $x^{\sqrt{x}}$ 

  , и становится больше функции $x^{\sqrt{x}}$ 

  .

• Для достаточно больших
  $x$ 

  , $x^{\sqrt{x}}$ 

  снова становится больше $x^2$ 

  .

Это даёт нам интересный взгляд на поведение этих функций на разных интервалах.