
Учебник «Алгебра» для 10-11 классов под авторством Алимова – это один из наиболее популярных и широко используемых учебных пособий для старшеклассников. Он заслужил признание как среди учителей, так и среди учеников благодаря своей структурированности, доступности изложения и качественной проработке материала.
ГДЗ по Алгебре 10-11 Класс Номер 175 Алимов — Подробные Ответы
Изобразить схематически график функции, указать её область определения и множество значений:
- у = х9;
- у = 7х4;
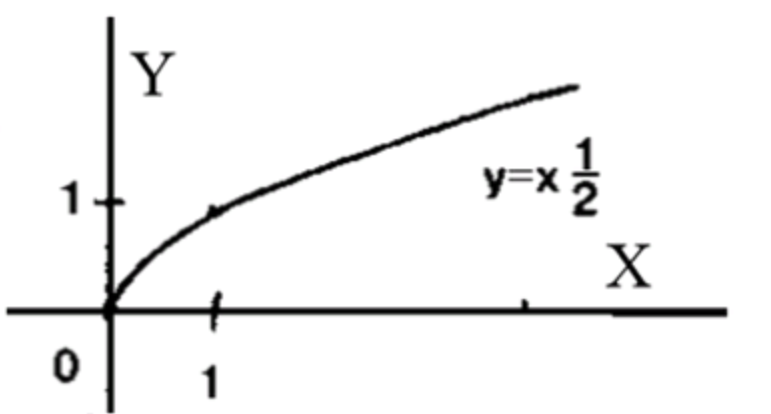
- у = корень x;
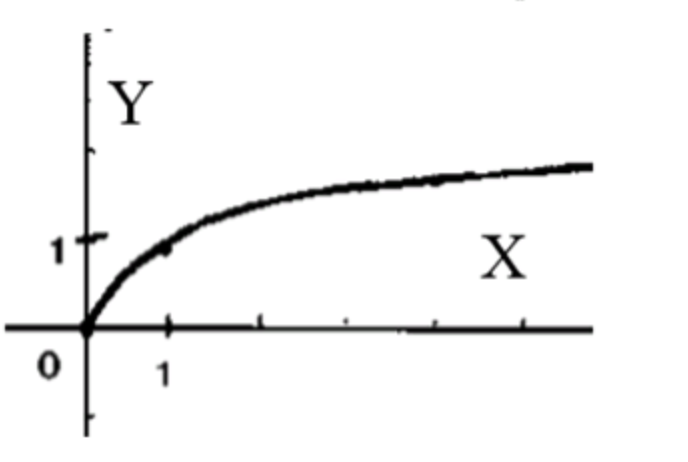
- у = корень 3 степени х;
- у = х ^ -2;
- у = х^-3.
1)
Показатель степени — нечетное натуральное число, значит:
Область определения функции:
Множество значений функции:
Схематический график функции:
2)
Показатель степени — четное натуральное число, значит:
Область определения функции:
Множество значений функции:
Схематический график функции:
3)
Показатель степени — положительное нецелое число, значит:
Область определения функции:
Область значения функции:
Схематический график функции:
4)
Показатель степени — положительное нецелое число, значит:
Область определения функции:
Область значения функции:
Схематический график функции:
5)
Показатель степени — отрицательное четное целое число, значит:
Область определения функции:
Множество значений функции:
Схематический график функции:
6)
Показатель степени — отрицательное нечетное целое число, значит:
Область определения функции:
Множество значений функции:
Схематический график функции:
1)
Показатель степени — нечетное натуральное число:
Когда показатель степени является нечетным натуральным числом, то функция будет определена на всей числовой оси (R) и её значения могут быть как положительными, так и отрицательными, в зависимости от значения .
- Если , то .
- Если , то .
- Если , то .
Область определения функции: , так как функция определена для любого действительного числа.
Множество значений функции: , так как для любого функция может принимать любое значение на числовой оси.
Схематический график функции:
График функции будет иметь форму кривой, проходящей через начало координат (точку
), и будет симметричен относительно начала координат. Для положительных график будет увеличиваться, а для отрицательных — уменьшаться, следуя характеристикам нечетных степеней.
2)
Показатель степени — четное натуральное число:
Когда показатель степени является четным числом, то для любых x, график функции будет всегда неотрицателен. Это означает, что для всех значений .
- Если , то .
- Если , то .
- Если , то , так как при возведении в четную степень отрицательное число дает положительный результат.
Область определения функции: , так как функция определена для всех действительных чисел.
Множество значений функции: , так как функция всегда неотрицательна. При любых значениях , результат всегда будет равен или больше нуля.
Схематический график функции:
- График будет симметричен относительно оси y (оси ), так как для положительных и отрицательных
- Он будет иметь форму параболы, которая будет направлена вверх, проходить через точку
, и для стремящихся к бесконечности, значение будет стремиться к бесконечности.
3)
Показатель степени — положительное нецелое число:
В этом случае, функция определена только для неотрицательных значений x, так как квадратный корень из отрицательного числа в действительных числах не существует.
- Если , то .
- Если , то .
Область определения функции: , так как для отрицательных значений выражение не имеет смысла в области действительных чисел.
Область значения функции: , так как квадратный корень всегда неотрицателен.
Схематический график функции:
График будет начинаться в точке (
4)
Показатель степени — положительное нецелое число:
Для кубического корня из x функция будет определена для всех значений , так как кубический корень из отрицательного числа существует.
- Если , то .
- Если , то .
- Если , то , так как кубический корень из отрицательного числа — отрицательное число.
Область определения функции: , так как функция определена для всех действительных чисел.
Область значения функции: , так как кубический корень может быть как положительным, так и отрицательным числом, в зависимости от знака .
Схематический график функции:
- График будет симметричен относительно начала координат, так как кубический корень из отрицательного числа также является отрицательным.
- График будет возрастать, но с более мягким наклоном, так как при увеличении x значения функции растут медленно.
5)
Показатель степени — отрицательное четное целое число:
При отрицательном четном показателе степени, функция определена для всех x, кроме нуля, так как деление на ноль невозможно.
- Если , то
- Если , то (так как возведение в четную степень делает результат положительным).
Область определения функции: , так как выражение не определено для .
Множество значений функции: , так как при любом значении , функция принимает положительные значения.
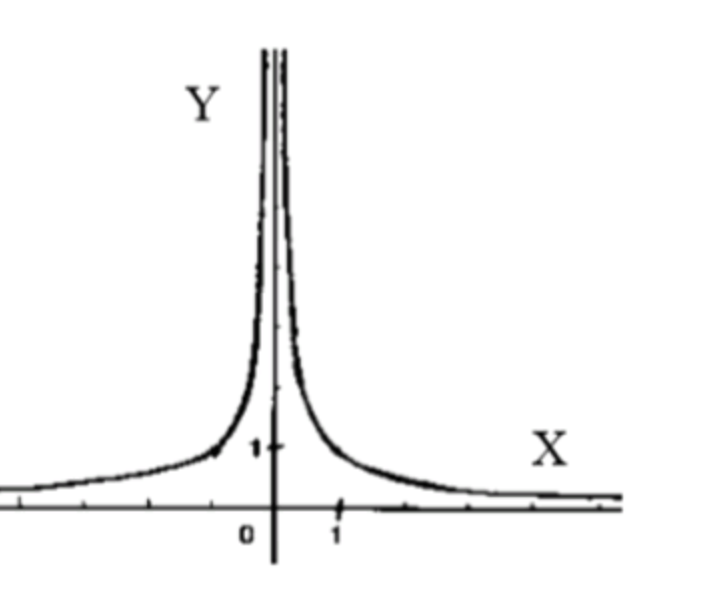
Схематический график функции:
- График будет стремиться к бесконечности при и будет симметричен относительно оси (оси
- Он будет уменьшаться при удалении от нуля, но всегда оставаться положительным.
6)
Показатель степени — отрицательное нечетное целое число:
Для функции с таким показателем степени, область определения снова будет всё R, за исключением нуля, так как деление на ноль невозможно.
- Если , то .
- Если , то , так как возведение в нечетную степень сохраняет знак.
Область определения функции: , так как функция не определена при .
Множество значений функции: , так как функция никогда не принимает значение ноль (при происходит деление на ноль).
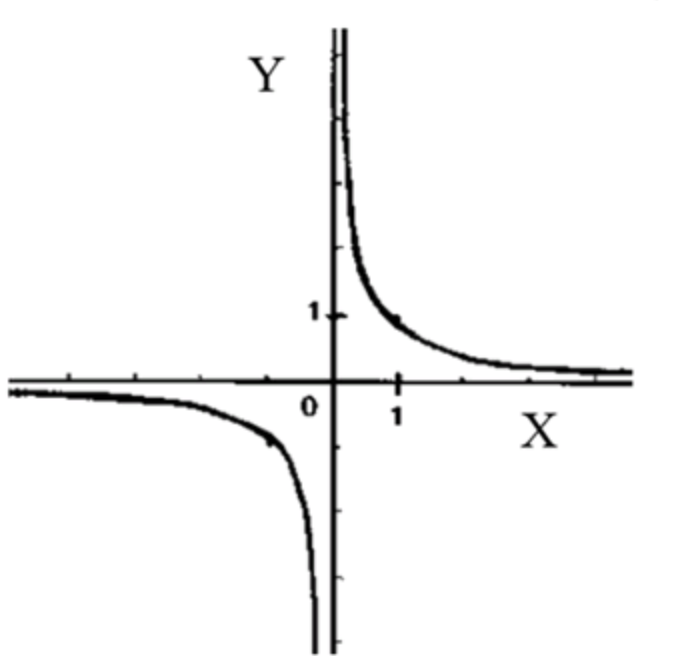
Схематический график функции:
- График будет проходить через начало координат и стремиться к бесконечности при , а к минус бесконечности при .
- Он будет симметричен относительно начала координат, и для положительных значений x он будет располагаться в верхней части, а для отрицательных — в нижней.


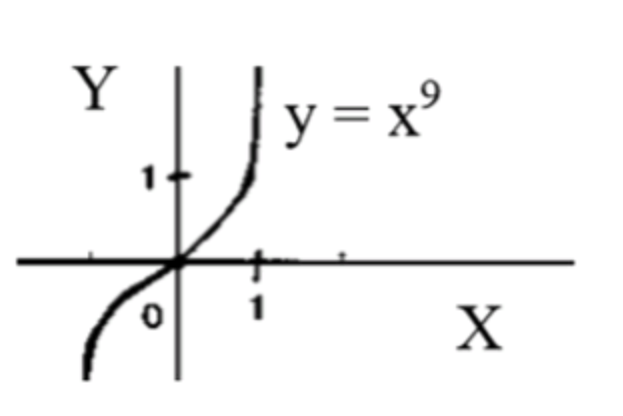
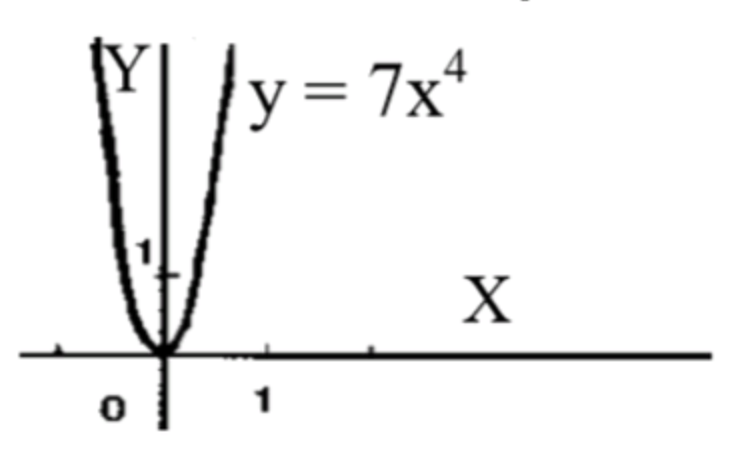

Оставь свой отзыв 💬
Комментариев пока нет, будьте первым!