ГДЗ по Алгебре 10-11 Класс Номер 173 Алимов — Подробные Ответы

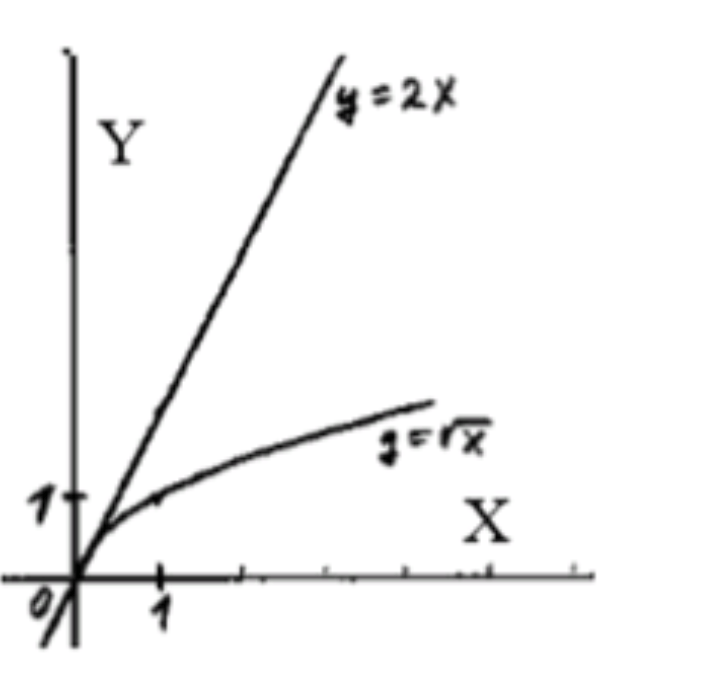
1. корень x < =2x;
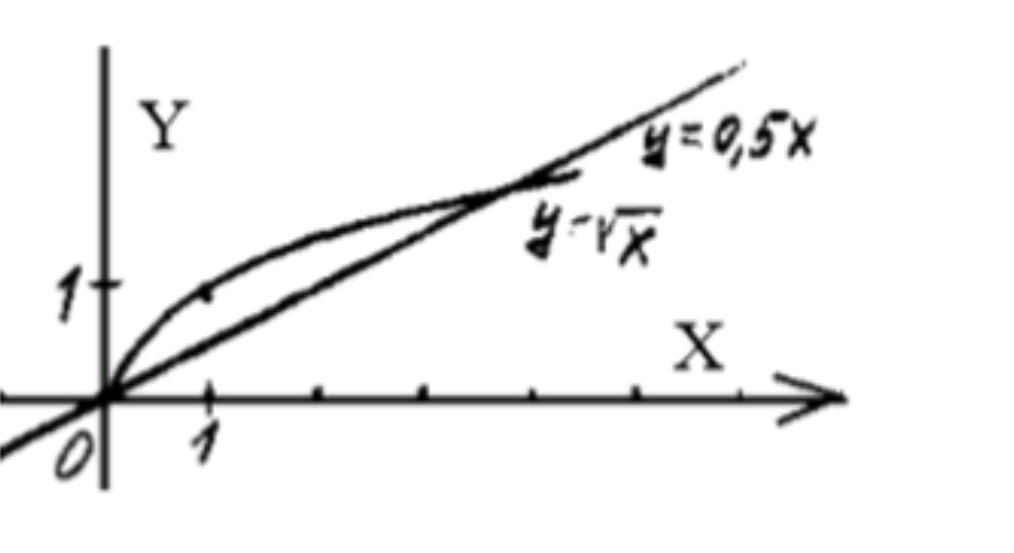
2. корень x > 0,5x;
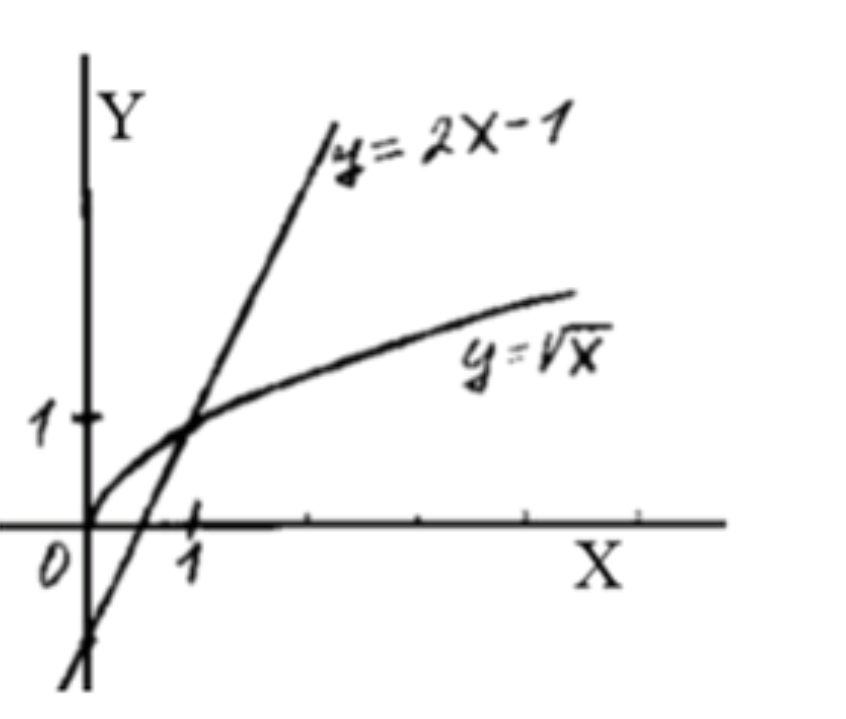
3. корень x > =2x-1;
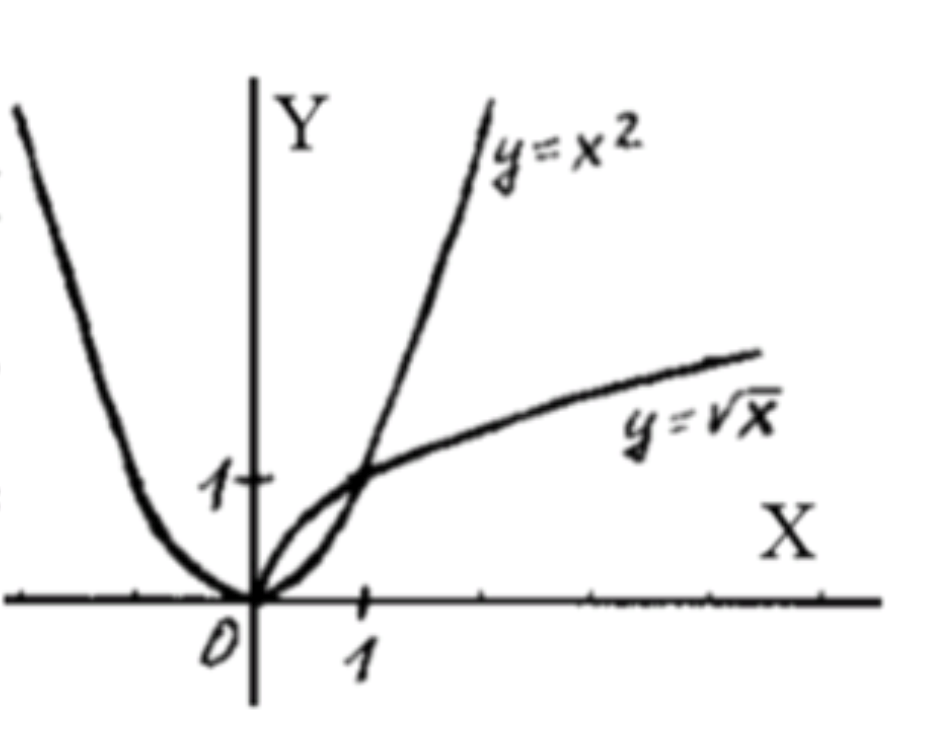
4. корень x > = x2.

1) $\sqrt{x} \leq 2x$

$y = \sqrt{x}$— уравнение ветви параболы:

$y = 2x$ — уравнение прямой:

Графики функций:

Ответ: $x\ge 0.25$

2) $\sqrt{x} > 0.5x$

$y = \sqrt{x}$— уравнение ветви параболы:

$y = 0.5x$ — уравнение прямой:

Графики функций:

Ответ: $0<x<4$

3) $\sqrt{x} \geq 2x — 1$

$y = \sqrt{x}$— уравнение ветви параболы:

$y = 2x — 1$ — уравнение прямой:

Графики функций:

Ответ: $0\le x\le 1$

$\mathrm{}$4) $\sqrt{x} \geq x^2$

$y = \sqrt{x}$— уравнение ветви параболы:

$y = x^2$ — уравнение параболы:

Графики функций:

Ответ: $0\le x\le 1$$\mathrm{}$

1) Решение неравенства $\sqrt{x} \leq 2x$

Шаг 1. Определим область допустимых значений (ОДЗ)

Функция $\sqrt{x}$определена при $x \geq 0$, а правая часть выражения $2x$ определена для всех $x$. Следовательно, область допустимых значений (ОДЗ) — $x \geq 0$.

Шаг 2. Возведение в квадрат

Возведём обе части неравенства в квадрат, чтобы избавиться от корня:

$$(\sqrt{x})^2 \leq (2x)^2$$

$$x \leq 4x^2$$

Шаг 3. Приведение к стандартному виду

Переносим всё в одну сторону:

$$4x^2 — x \geq 0$$

Шаг 4. Решение квадратного неравенства

Рассмотрим квадратное уравнение:

$$4x^2 — x = 0$$

Вынесем общий множитель $x$:

$$x(4x — 1) = 0$$

Найдём корни:

$$x = 0, \quad 4x — 1 = 0 \Rightarrow x = \frac{1}{4}$$

Шаг 5. Анализ знаков

Рассмотрим произведение $x(4x — 1)$ на числовой оси:

• При $x<0$ знак отрицательный (не подходит, так как $x\ge 0$).
• При $0<x<\frac{1}{4}$ знак отрицательный.
• При $x>\frac{1}{4}$ знак положительный (подходит).

Так как нам нужно $4x^2 — x \geq 0$, выбираем промежуток:

$$x \geq \frac{1}{4}$$

Шаг 6. Запись ответа$$x \geq 0.25$$

2) Решение неравенства $\sqrt{x} > 0.5x$

Шаг 1. Определим область допустимых значений (ОДЗ)

Корень определён при $x \geq 0$, поэтому ОДЗ: $x \geq 0$.

Шаг 2. Возведение в квадрат

Квадрат обеих частей:

$$(\sqrt{x})^2 > (0.5x)^2$$

$$x > 0.25x^2$$

Шаг 3. Приведение к стандартному виду

$$0.25x^2 — x < 0$$

Шаг 4. Решение квадратного неравенства

Рассмотрим уравнение:

$$0.25x^2 — x = 0$$

Вынесем общий множитель:

$$x(0.25x — 1) = 0$$

Корни уравнения:

$$x = 0, \quad 0.25x — 1 = 0 \Rightarrow x = 4$$

Шаг 5. Анализ знаков

Промежутки:

• При $x<0$ знак отрицательный (не учитываем из-за ОДЗ).
• При $0<x<4$ знак положительный (подходит).
• При $x>4$ знак отрицательный.

Так как нам нужно $0.25x^2 — x < 0$, выбираем:

$$0 < x < 4$$

Шаг 6. Запись ответа$$0 < x < 4$$

3) Решение неравенства $\sqrt{x} \geq 2x — 1$

Шаг 1. Определим область допустимых значений (ОДЗ)

ОДЗ:

• $\sqrt{x}$определено при $x \geq 0$.
• $2x — 1$ должно быть неотрицательным:

$$2x — 1 \geq 0 \Rightarrow x \geq \frac{1}{2}$$

Общая ОДЗ: $x\ge 0$.

Шаг 2. Возведение в квадрат

$$(\sqrt{x})^2 \geq (2x — 1)^2$$

$$x \geq 4x^2 — 4x + 1$$

Шаг 3. Приведение к стандартному виду

$$4x^2 — 5x + 1 \leq 0$$

Шаг 4. Решение квадратного неравенства

Дискриминант:

$$D = (-5)^2 — 4 \cdot 4 \cdot 1 = 25 — 16 = 9$$

Корни:

$$x_{1,2} = \frac{5 \pm 3}{8}$$

$$x_1 = \frac{5 — 3}{8} = \frac{2}{8} = \frac{1}{4}, \quad x_2 = \frac{5 + 3}{8} = \frac{8}{8} = 1$$

Шаг 5. Анализ знаков

Квадратный трёхчлен $4x^2 — 5x + 1$ принимает отрицательные значения между корнями:

$$\frac{1}{4} \leq x \leq 1$$

С учётом ОДЗ: $x \geq 0$, окончательный ответ:

$$0 \leq x \leq 1$$

4) Решение неравенства $\sqrt{x} \geq x^2$

Шаг 1. Определим область допустимых значений (ОДЗ)

ОДЗ: $x \geq 0$.

Шаг 2. Возведение в квадрат

$$(\sqrt{x})^2 \geq (x^2)^2$$

$$x \geq x^4$$

Шаг 3. Приведение к стандартному виду

$$x — x^4 \geq 0$$

Шаг 4. Разложение на множители

$$x(1 — x^3) \geq 0$$

Рассматриваем уравнение $1 — x^3 = 0$:

$$x^3 = 1 \Rightarrow x = 1$$

Шаг 5. Анализ знаков

• При $x<1$ знак $(1-x^3)$положительный, $x$$$ положительный.
• При $x>1$ знак $(1-x^3)$ отрицательный.

Тогда:

$$0 \leq x \leq 1$$

Шаг 6. Запись ответа$$0 \leq x \leq 1$$