
Учебник «Алгебра» для 10-11 классов под авторством Алимова – это один из наиболее популярных и широко используемых учебных пособий для старшеклассников. Он заслужил признание как среди учителей, так и среди учеников благодаря своей структурированности, доступности изложения и качественной проработке материала.
ГДЗ по Алгебре 10-11 Класс Номер 172 Алимов — Подробные Ответы
Решить графически неравенство (172-173).
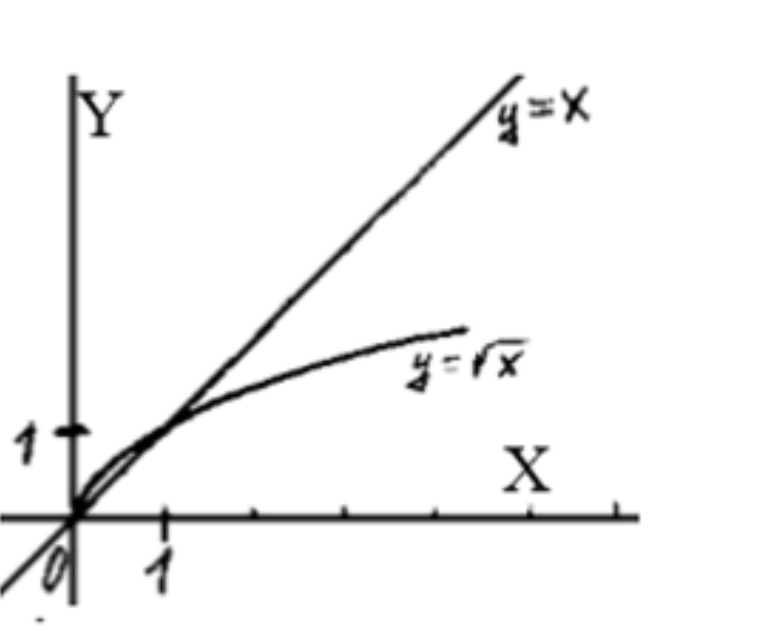
- корень x > =x;
- корень x < x;
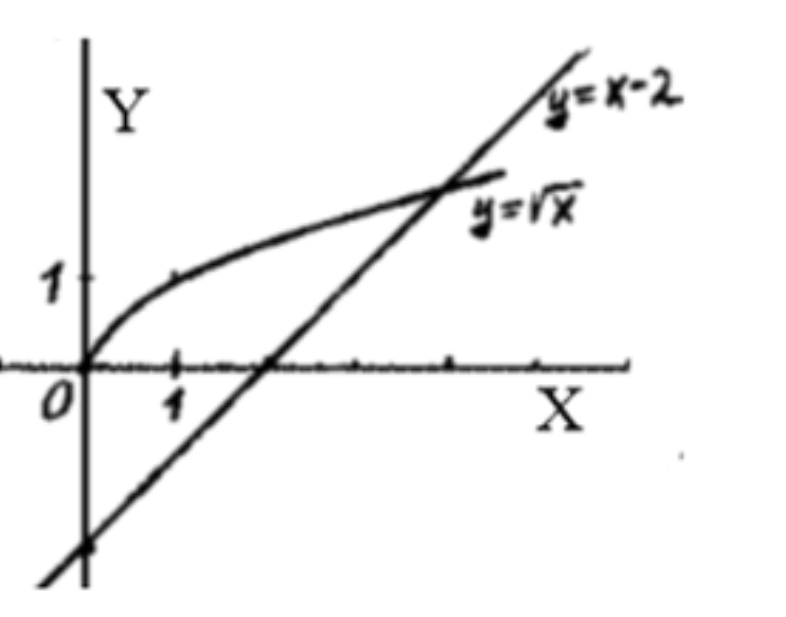
- корень x > =2x-1;
- корень x > =x2.
1)
— уравнение ветви параболы:
|
| 0 | 1 | 4 | 9 |
|---|---|---|---|---|
|
| 0 | 1 | 2 | 3 |
— уравнение прямой:
|
| 0 | 1 |
|---|---|---|
|
| 0 | 1 |
Ответ:
2)
— уравнение ветви параболы:
|
| 0 | 1 | 4 | 9 |
|---|---|---|---|---|
|
| 0 | 1 | 2 | 3 |
— уравнение прямой:
|
| 0 | 1 |
|---|---|---|
|
| 0 | 1 |
Ответ:
3)
— уравнение ветви параболы:
|
| 0 | 1 | 4 | 9 |
|---|---|---|---|---|
|
| 0 | 1 | 2 | 3 |
— уравнение прямой:
|
| 0 | 1 |
|---|---|---|
|
| -2 | -1 |
Ответ:
4)
— уравнение ветви параболы:
|
| 0 | 1 | 4 | 9 |
|---|---|---|---|---|
|
| 0 | 1 | 2 | 3 |
— уравнение прямой:
|
| 0 | 1 |
|---|---|---|
|
| -2 | -1 |
Ответ:
Задача 1:
Рассмотрим неравенство:
1. Область допустимых значений (ОДЗ)
Функция определена только при , так как подкоренное выражение должно быть неотрицательным.
2. Решение методом возведения в квадрат
Так как оба выражения в неравенстве неотрицательны при , возводим обе части в квадрат:
3. Решение квадратного неравенства
Рассмотрим параболу . Она пересекает ось в точках:
Так как коэффициент при отрицательный (), ветви параболы направлены вниз. Неравенство выполняется между корнями:
Ответ:
Задача 2:
Рассмотрим неравенство:
1. Область допустимых значений (ОДЗ)
Функция определена только при .
2. Возведение в квадрат
Так как обе части неотрицательны при , возводим обе части в квадрат:
3. Решение квадратного неравенства
Как и в предыдущей задаче, парабола пересекает ось в точках и . Так как ветви направлены вниз, неравенство выполняется на интервале:
Ответ:
Задача 3:
Рассмотрим неравенство:
1. Область допустимых значений (ОДЗ)
Функция определена при .
2. Возведение в квадрат
Возводим обе части в квадрат (так как обе части неотрицательны при ):
3. Решение квадратного неравенства
Рассмотрим квадратное уравнение:
Находим корни по теореме Виета:
Получаем точки пересечения и . Так как коэффициент при положительный, ветви параболы направлены вверх. Неравенство выполняется между корнями:
С учетом ОДЗ (), добавляем точку 0:
Ответ:
Задача 4:
Рассмотрим неравенство:
1. Область допустимых значений (ОДЗ)
Функция определена при . Также выражение должно быть неотрицательным, так как корень не может быть больше отрицательного числа:
Таким образом, ОДЗ:
2. Возведение в квадрат
Возведем обе части в квадрат:
3. Решение квадратного неравенства
Рассматриваем уравнение:
Его корни:
Так как коэффициент при положительный, ветви параболы направлены вверх. Неравенство выполняется вне корней:
4. Учет ОДЗ
С учетом остается только .
Ответ:



Оставь свой отзыв 💬
Комментариев пока нет, будьте первым!