ГДЗ по Алгебре 10-11 Класс Номер 1592 Алимов — Подробные Ответы

Найти площадь фигуры, ограниченной параболой $y=0,5x^2-2x+2$ и касательными к ней, проведенными через точки $A(1;\frac{1}{2})$ и $B(4;2)$.

Дана функция:

$$f(x)=0.5x^2-2x+2;$$

Производная функции:

$$f^{\mathrm{\prime }}(x)=0.5(x^2{)}^{\mathrm{\prime }}-(2x-2{)}^{\mathrm{\prime }}=0.5\cdot 2x-2=x-2;$$

Уравнение касательной в точке $A(1;\frac{1}{2})$:

$$f^{\mathrm{\prime }}(1)=1-2=-1;$$$$f(1)=0.5\cdot 1^2-2\cdot 1+2=0.5-2+2=0.5;$$$$y=0.5-1(x-1)=0.5-x+1=1.5-x;$$

Уравнение касательной в точке $B(4;2)$:

$$f^{\mathrm{\prime }}(4)=4-2=2;$$$$f(4)=0.5\cdot 4^2-2\cdot 4+2=8-8+2=2;$$$$y=2+2(x-4)=2+2x-8=2x-6;$$

Абсцисса пересечения касательных:

$$1.5-x=2x-6;$$$$-3x=-7.5,\text{ отсюда }x=2.5;$$

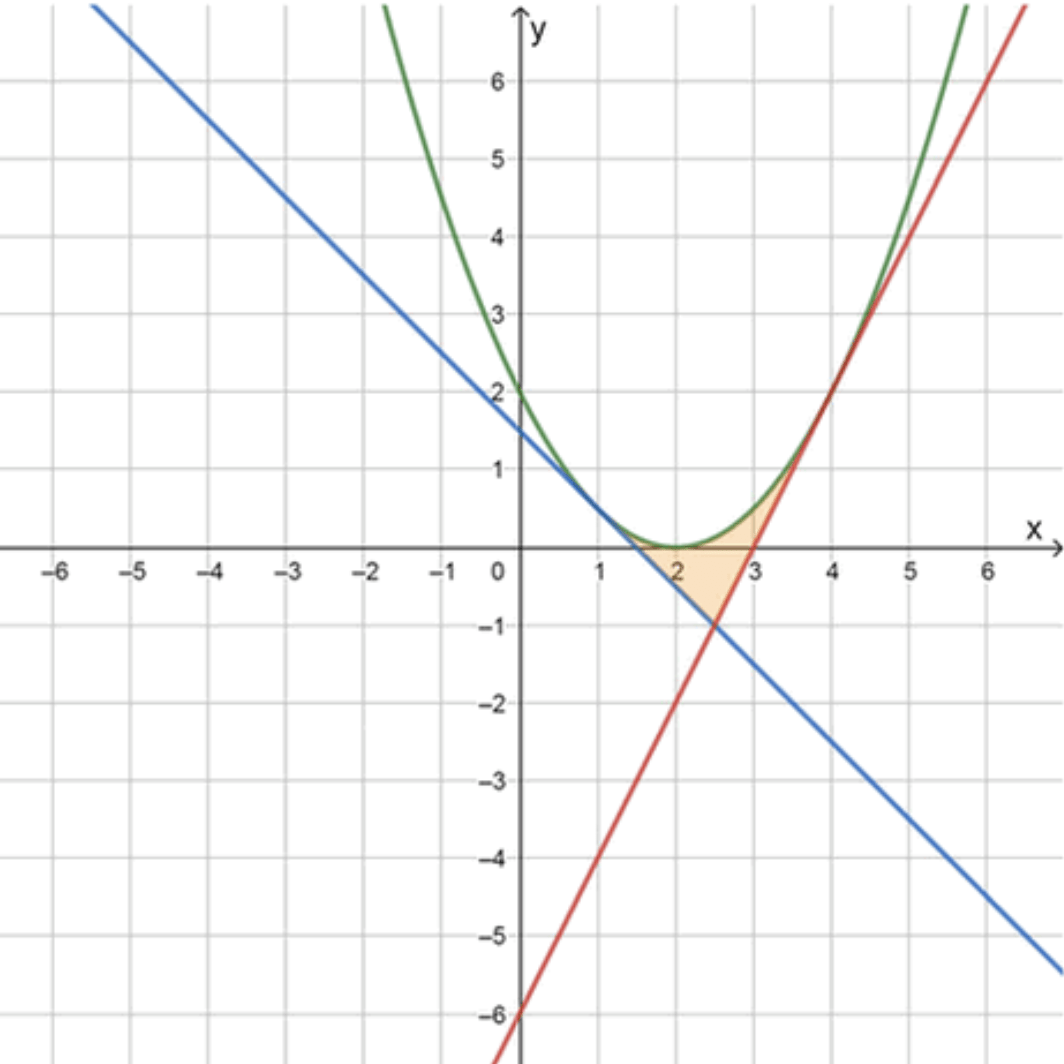
Графики функций:

Площадь криволинейной трапеции:

$${\int }_1^{2.5}(0.5x^2-2x+2-1.5+x)+{\int }_{2.5}^4(0.5x^2-2x+2-2x+6)=$$$$={\int }_1^{2.5}(0.5x^2-x+0.5)+{\int }_{2.5}^4(0.5x^2-4x+8)=$$$$=(0.5\cdot \frac{x^3}{3}-\frac{x^2}{2}+0.5\cdot \frac{x^1}{1}){\mid }_1^{2.5}+(0.5\cdot \frac{x^3}{3}-4\cdot \frac{x^2}{2}+8\cdot \frac{x^1}{1}){\mid }_{2.5}^4=$$$$=(\frac{x^3}{6}-\frac{x^2}{2}+\frac{x}{2}){\mid }_1^{2.5}+(\frac{x^3}{6}-2x^2+8x){\mid }_{2.5}^4=$$$$=(\frac{{\left(\frac{5}{2}\right)}^3}{6}-\frac{{\left(\frac{5}{2}\right)}^2}{2}+\frac{\frac{5}{2}}{2})-(\frac{1^3}{6}-\frac{1^2}{2}+\frac{1}{2})+$$

$$+(\frac{4^3}{6}-2\cdot 4^2+8\cdot 4)-(\frac{{\left(\frac{5}{2}\right)}^3}{6}-2\cdot {\left(\frac{5}{2}\right)}^2+8\cdot \frac{5}{2})=$$$$=(-\frac{25}{4\cdot 2}+\frac{5}{4}-\frac{1}{6}+\frac{1}{2}-\frac{1}{2}+\frac{64}{6}-2\cdot 16+32+\frac{2\cdot 25}{4}-\frac{40}{2})=$$$$=(-\frac{25}{8}+\frac{5}{4}+\frac{63}{6}-32+32+\frac{50}{4}-\frac{40}{2})=-\frac{25}{8}+\frac{55}{4}-\frac{80}{4}+\frac{21}{2}=$$$$=\frac{-25-50+84}{8}=\frac{9}{8}=1\frac{1}{8};$$

Ответ: $1\frac{1}{8}$.

Дана парабола $y=0.5x^2-2x+2$, а также касательные к графику этой функции, проведенные через точки $A(1;0.5)$ и $B(4;2)$. Необходимо найти площадь фигуры, ограниченной параболой и касательными.

Шаг 1: Вычисление производной функции

Для нахождения касательных к графику функции, сначала вычислим производную функции $y=0.5x^2-2x+2$. Это нужно для определения угловых коэффициентов касательных.

Функция:

$$f(x)=0.5x^2-2x+2$$

Найдем производную $f^{\mathrm{\prime }}(x)$ с использованием стандартных правил дифференцирования:

$$f^{\mathrm{\prime }}(x)=0.5\cdot 2x-2=x-2$$

Таким образом, производная функции $f^{\mathrm{\prime }}(x)=x-2$ определяет угловой коэффициент касательных к графику функции.

Шаг 2: Уравнение касательной в точке $A(1;0.5)$

Касательная к графику функции в точке $A(1;0.5)$ имеет угловой коэффициент $f^{\mathrm{\prime }}(1)$, который мы найдем, подставив $x=1$ в производную:

$$f^{\mathrm{\prime }}(1)=1-2=-1$$

Теперь вычислим значение функции в точке $A(1)$:

$$f(1)=0.5\cdot 1^2-2\cdot 1+2=0.5-2+2=0.5$$

Итак, точка $A(1;0.5)$ действительно лежит на графике функции. Теперь, зная угловой коэффициент касательной и координаты точки, можем найти уравнение касательной в этой точке. Уравнение касательной имеет вид:

$$y-y_1=f^{\mathrm{\prime }}(x_1)(x-x_1)$$

Подставляем координаты точки $A(1;0.5)$ и угловой коэффициент $f^{\mathrm{\prime }}(1)=-1$:

$$y-0.5=-1(x-1)$$

Раскроем скобки:

$$y-0.5=-x+1$$

Переносим все на одну сторону:

$$y=1.5-x$$

Таким образом, уравнение касательной в точке $A$ имеет вид:

$$y=1.5-x$$

Шаг 3: Уравнение касательной в точке $B(4;2)$

Теперь найдем уравнение касательной в точке $B(4;2)$. Для этого вычислим угловой коэффициент $f^{\mathrm{\prime }}(4)$:

$$f^{\mathrm{\prime }}(4)=4-2=2$$

Теперь вычислим значение функции в точке $B(4)$:

$$f(4)=0.5\cdot 4^2-2\cdot 4+2=8-8+2=2$$

Итак, точка $B(4;2)$ действительно лежит на графике функции. Теперь, используя угловой коэффициент $f^{\mathrm{\prime }}(4)=2$ и координаты точки $B(4;2)$, находим уравнение касательной в этой точке:

$$y-2=2(x-4)$$

Раскроем скобки:

$$y-2=2x-8$$

Переносим все на одну сторону:

$$y=2x-6$$

Таким образом, уравнение касательной в точке $B$ имеет вид:

$$y=2x-6$$

Шаг 4: Абсцисса пересечения касательных

Найдем точку пересечения касательных. Для этого приравняем уравнения касательных $y=1.5-x$ и $y=2x-6$:

$$1.5-x=2x-6$$

Решим это уравнение:

$$1.5+6=2x+x$$$$7.5=3x$$$$x=\frac{7.5}{3}=2.5$$

Таким образом, абсцисса точки пересечения касательных равна $x=2.5$.

Шаг 5: Площадь фигуры

Теперь, когда мы нашли точку пересечения касательных $x=2.5$, можем вычислить площадь фигуры, ограниченной параболой и касательными. Фигура представляет собой криволинейную трапецию, которая ограничена двумя касательными и кривой функции $f(x)$.

Для нахождения площади этой фигуры используем определенные интегралы. Площадь можно вычислить как сумму двух интегралов: один от $x=1$ до $x=2.5$, а второй — от $x=2.5$ до $x=4$. Мы будем вычитать функцию касательной из функции параболы, чтобы получить площадь между ними.

Площадь можно выразить как:

$$S={\int }_1^{2.5}(f(x)-(1.5-x))dx+{\int }_{2.5}^4(f(x)-(2x-6))dx$$

Преобразуем выражения для интегралов:

Первый интеграл:

$${\int }_1^{2.5}(0.5x^2-2x+2-1.5+x)dx={\int }_1^{2.5}(0.5x^2-x+0.5)dx$$

Второй интеграл:

$${\int }_{2.5}^4(0.5x^2-2x+2-2x+6)dx={\int }_{2.5}^4(0.5x^2-4x+8)dx$$

Теперь интегрируем обе функции по частям.

Интеграл 1:

$$\int (0.5x^2-x+0.5)dx=\frac{0.5x^3}{3}-\frac{x^2}{2}+0.5x$$

Вычисляем значение этого интеграла от $x=1$ до $x=2.5$:

$$(\frac{0.5x^3}{3}-\frac{x^2}{2}+0.5x){\mid }_1^{2.5}$$

Интеграл 2:

$$\int (0.5x^2-4x+8)dx=\frac{0.5x^3}{3}-\frac{4x^2}{2}+8x$$

Вычисляем значение этого интеграла от $x=2.5$ до $x=4$:

$$(\frac{0.5x^3}{3}-\frac{4x^2}{2}+8x){\mid }_{2.5}^4$$

После подстановки значений и вычислений получаем окончательный результат для площади:

$$S=1\frac{1}{8}\mathrm{.}$$

Ответ:

Площадь фигуры, ограниченной параболой и касательными, равна $1\frac{1}{8}$.