
Учебник «Алгебра» для 10-11 классов под авторством Алимова – это один из наиболее популярных и широко используемых учебных пособий для старшеклассников. Он заслужил признание как среди учителей, так и среди учеников благодаря своей структурированности, доступности изложения и качественной проработке материала.
ГДЗ по Алгебре 10-11 Класс Номер 1535 Алимов — Подробные Ответы
Исследовать функцию у = f (х) и построить её график (1535—1537).
- f(х) = 4х3 + 6х2;
- f (х) = 3х2 — 2х3.
1) ;
- Функция ни четная, ни нечетная:
- Производная функции:
- Промежуток возрастания:
- Промежуток убывания:
- Стационарные точки:
- Максимум и минимум функции:
- Координаты некоторых точек:
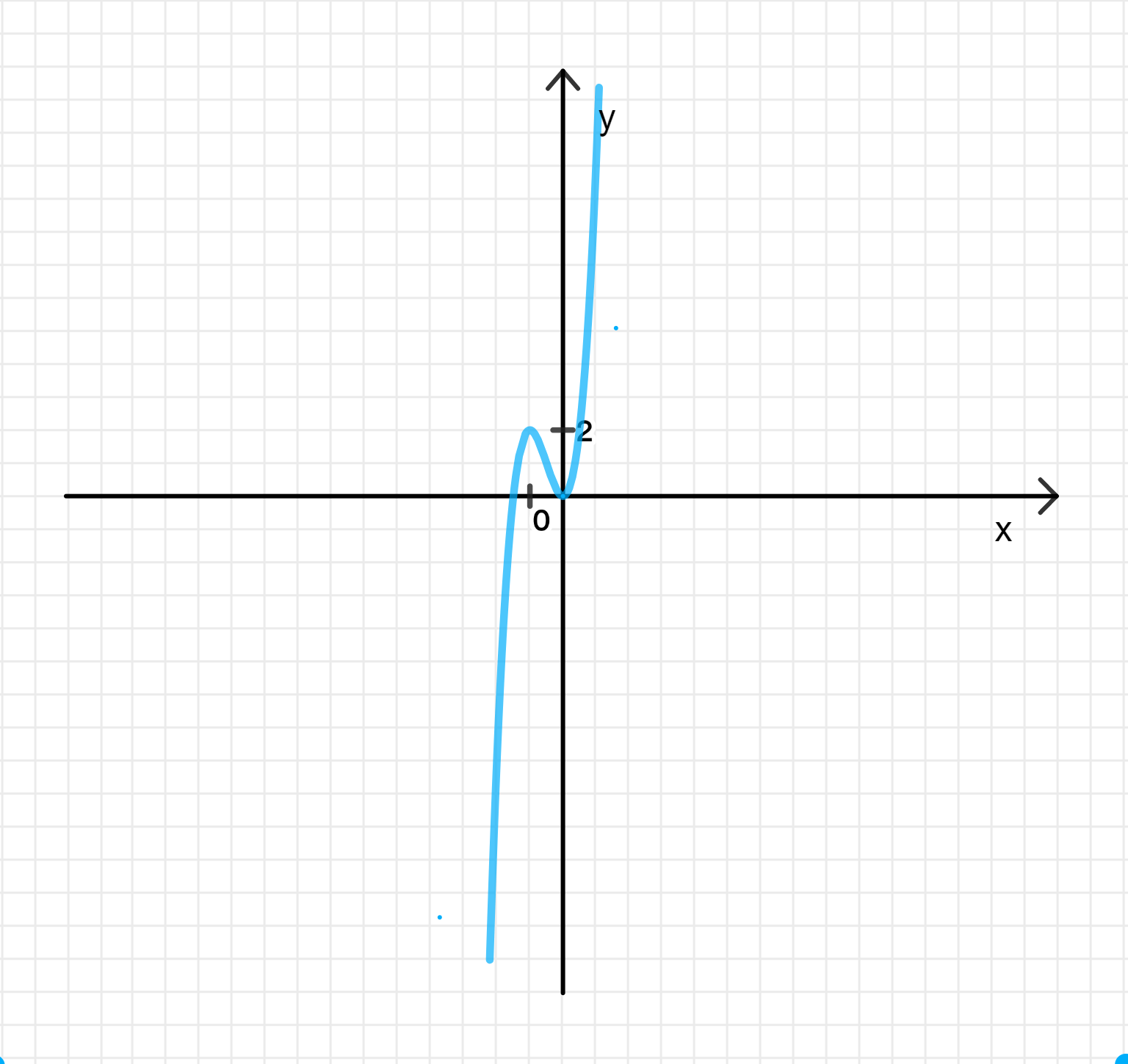
График функции:
2) ;
- Функция ни четная, ни нечетная:
- Производная функции:
- Промежуток возрастания:
- Промежуток убывания:
- Стационарные точки:
- Максимум и минимум функции:
- Координаты некоторых точек:
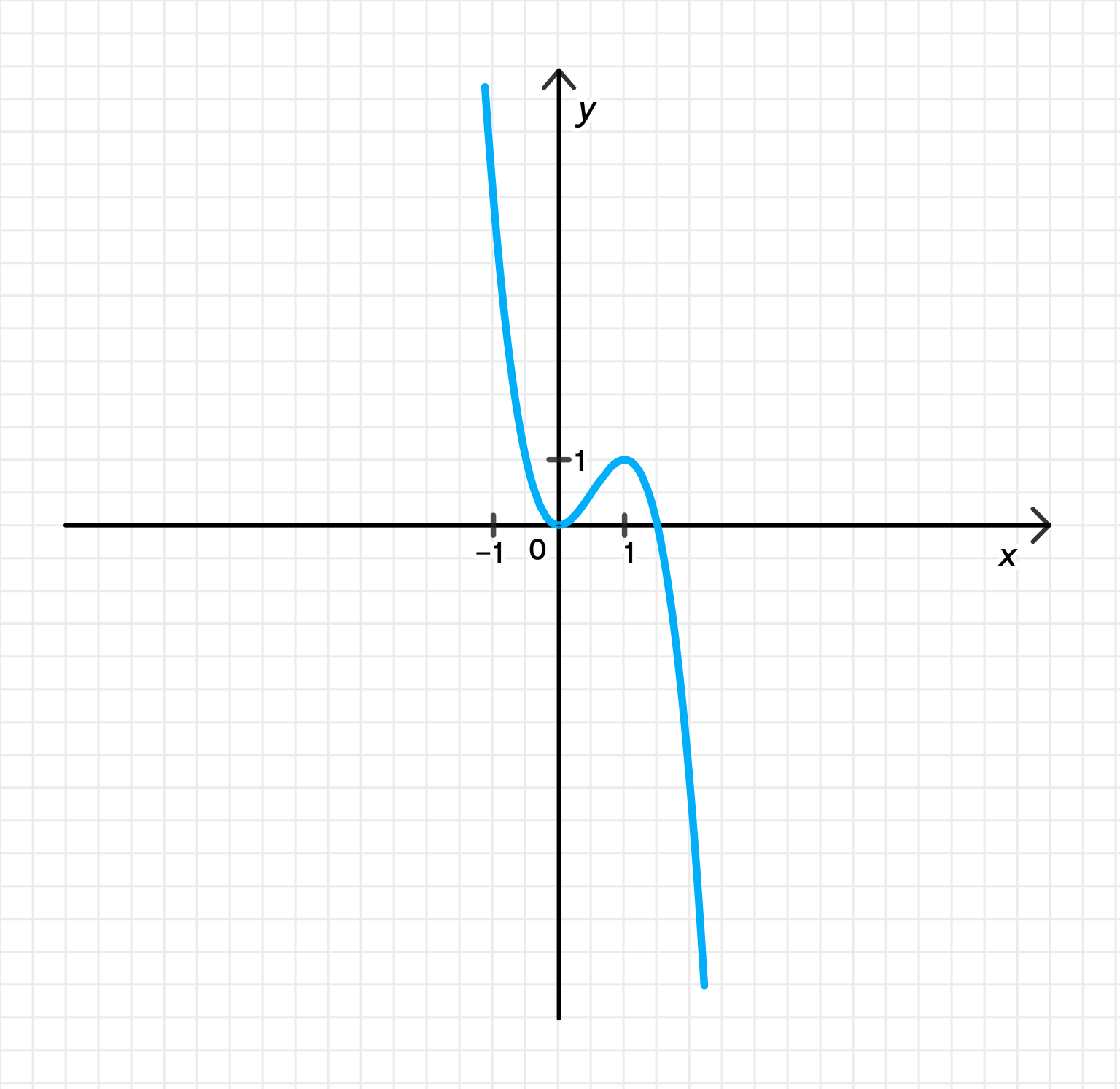
График функции:
1)
Шаг 1: Проверяем четность и нечетность функции
Четность и нечетность функции определяется следующим образом:
- Функция четная, если для всех .
- Функция нечетная, если для всех .
Проверим, является ли функция четной или нечетной.
- Подставим вместо в функцию:
- Сравниваем с :
Мы видим, что и , следовательно, функция ни четная, ни нечетная.
Шаг 2: Находим производную функции
Для нахождения производной функции используем стандартные правила дифференцирования:
- Производная от по равна .
Таким образом, дифференцируем каждый член:
Получаем:
Шаг 3: Находим промежутки возрастания и убывания
Чтобы найти промежутки возрастания и убывания, нужно решить неравенство для возрастания и для убывания.
Решаем неравенство:
Вынесем общий множитель :
Теперь решаем неравенство:
Это произведение больше нуля, когда оба множителя либо положительны, либо оба отрицательны.
Критические точки: и .
Теперь исследуем знак произведения на промежутках , , .
- Для , например, :
Значит, на промежутке функция возрастает.
- Для , например, :
Значит, на промежутке функция убывает.
- Для , например, :
Значит, на промежутке функция возрастает.
Итак, промежутки возрастания: и , промежуток убывания: .
Шаг 4: Находим стационарные точки
Стационарные точки находятся при .
Решим уравнение:
Вынесем общий множитель :
Критические точки: и .
Точка — точка максимума, точка — точка минимума.
Шаг 5: Находим максимум и минимум функции
Для :
Точка максимума: .
Для :
Точка минимума: .
Шаг 6: Координаты некоторых точек
Теперь вычислим значения функции для нескольких точек:
- Для :
- Для :
Таким образом, таблица значений функции:
Шаг 7: График функции
2)
Шаг 1: Проверяем четность и нечетность функции
Аналогично первому примеру, проверяем, является ли функция четной или нечетной.
- Подставим вместо :
- Сравниваем с :
Мы видим, что и , следовательно, функция ни четная, ни нечетная.
Шаг 2: Находим производную функции
Дифференцируем :
Получаем:
Шаг 3: Находим промежутки возрастания и убывания
Решаем неравенство :
Вынесем общий множитель :
Теперь решаем неравенство:
Это произведение больше нуля, когда и имеют разные знаки.
Критические точки: и .
Теперь исследуем знак на промежутках , , .
- Для , например, :
Значит, на промежутке функция возрастает.
- Для , например, :
Значит, на промежутке функция убывает.
- Для , например, :
Значит, на промежутке функция убывает.
Итак, промежутки возрастания: , промежутки убывания: и .
Шаг 4: Находим стационарные точки
Стационарные точки находятся при :
Вынесем общий множитель:
Критические точки: и .
Точка — точка максимума, точка — точка минимума.
Шаг 5: Находим максимум и минимум функции
Для :
Точка максимума: .
Для :
Точка минимума: .
Шаг 6: Координаты некоторых точек
Вычислим значения функции для нескольких точек:
- Для :
- Для :
Таблица значений:
Шаг 7: График функции



Оставь свой отзыв 💬
Комментариев пока нет, будьте первым!