ГДЗ по Алгебре 10-11 Класс Номер 1533 Алимов — Подробные Ответы

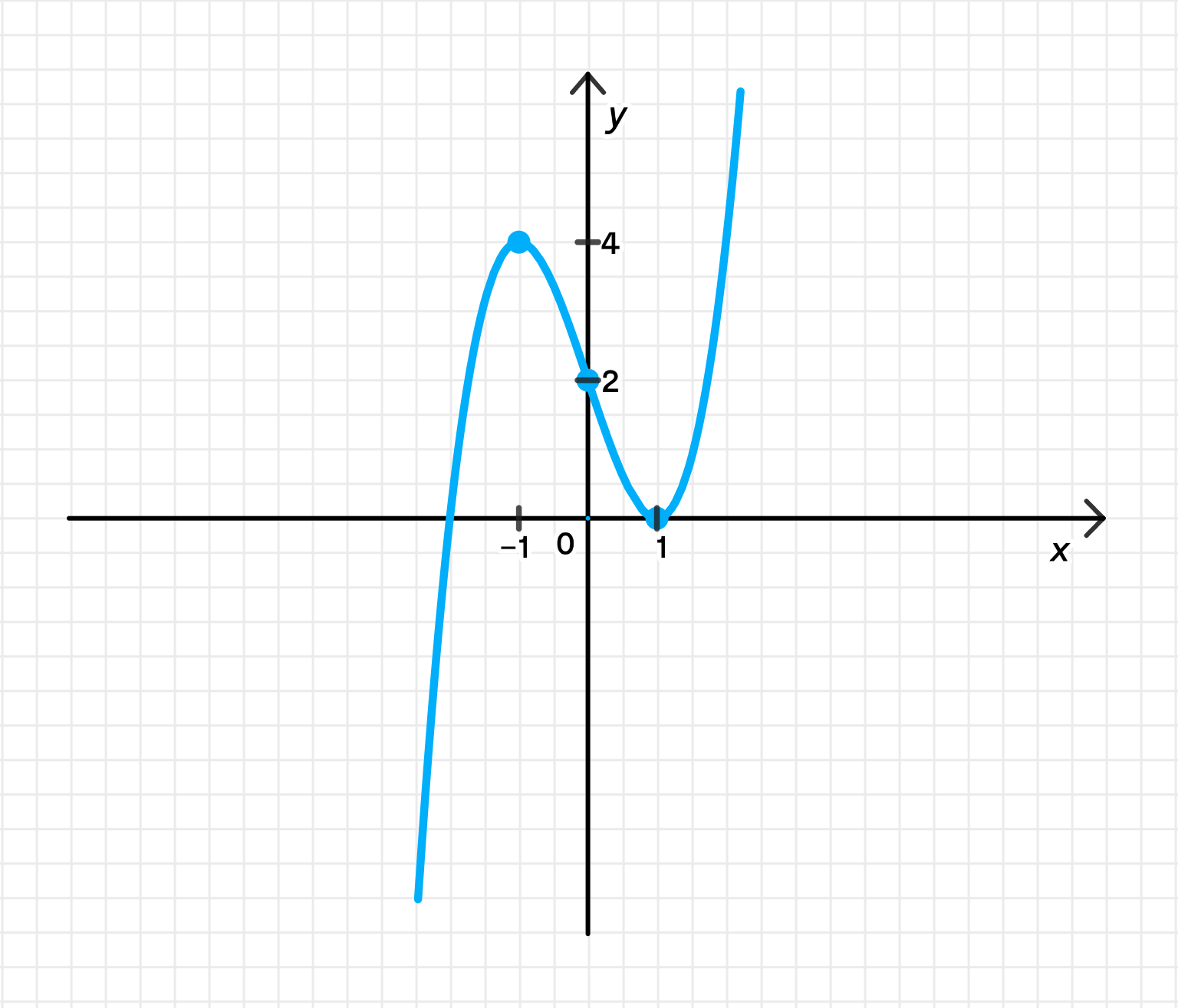
Исследовать с помощью производной функцию у = x3 — 3x + 2 и построить её график. Найти точки, в которых касательные к графику параллельны оси Ох.

Дана функция: $y = x^3 — 3x + 2$;

Производная функции:
$y'(x) = (x^3)’ — (3x — 2)’ = 3x^2 — 3;$

Промежуток возрастания:
$3x^2 — 3 > 0;$
$x^2 — 1 > 0;$
$x^2 > 1;$
$x < -1 \text{ и } x > 1;$

Промежуток убывания:
$-1 < x < 1;$

Критические точки:
$x = -1 \text{ — точка максимума; }$
$x = 1 \text{ — точка минимума; }$

Максимум и минимум функции:
$y(-1) = (-1)^3 — 3 \cdot (-1) + 2 = -1 + 3 + 2 = 4;$
$y(1) = 1^3 — 3 \cdot 1 + 2 = 1 — 3 + 2 = 0;$

Координаты некоторых точек:

График функции:

Касательная параллельна оси $Ox$, если $y'(x) = 0$:
$(-1; 4) \text{ и } (1; 0).$

Функция:

$$y = x^3 — 3x + 2$$

Нам нужно провести анализ этой функции: найти критические точки, промежутки возрастания и убывания, а также найти максимумы и минимумы.

Шаг 1: Находим производную функции

Для того чтобы исследовать поведение функции, начнем с нахождения её производной. Мы используем стандартные правила дифференцирования:

• Производная $x^n$ по $x$ равна $n \cdot x^{n-1}$,
• Производная от линейной функции $ax$ равна $a$,
• Производная от константы равна 0.

Применим эти правила к каждому слагаемому функции $y = x^3 — 3x + 2$:

$$y'(x) = \frac{d}{dx}(x^3) — \frac{d}{dx}(3x) + \frac{d}{dx}(2)$$ $$y'(x) = 3x^2 — 3$$

Теперь у нас есть выражение для производной функции:

$$y'(x) = 3x^2 — 3$$

Шаг 2: Определяем промежутки возрастания и убывания

Чтобы найти, на каких промежутках функция возрастает или убывает, нужно исследовать знак производной. Сначала решим неравенство $y'(x) > 0$ для промежутков возрастания и $y'(x) < 0$ для промежутков убывания.

Промежуток возрастания:

Мы ищем, когда производная больше нуля:

$$3x^2 — 3 > 0$$

Для того чтобы решить это неравенство, сначала упростим его:

$$x^2 — 1 > 0$$

Раскроем это как разность квадратов:

$$(x — 1)(x + 1) > 0$$

Для решения этого неравенства используем метод интервалов. Критическими точками являются $x = 1$ и $x = -1$. Теперь делим числовую прямую на интервалы: $(-\infty, -1)$, $(-1, 1)$, $(1, \infty)$. Проверим знак выражения $(x — 1)(x + 1)$ на этих промежутках:

• Для $x \in (-\infty, -1)$, например, $x = -2$:

  $$(-2 — 1)(-2 + 1) = (-3)(-1) = 3 > 0$$

  Значит, на промежутке $(-\infty, -1)$ функция возрастает.

• Для $x \in (-1, 1)$, например, $x = 0$:

  $$(0 — 1)(0 + 1) = (-1)(1) = -1 < 0$$

  Значит, на промежутке $(-1, 1)$ функция убывает.

• Для $x \in (1, \infty)$, например, $x = 2$:

  $$(2 — 1)(2 + 1) = (1)(3) = 3 > 0$$

  Значит, на промежутке $(1, \infty)$ функция снова возрастает.

Таким образом, функция возрастает на промежутках $(-\infty, -1)$ и $(1, \infty)$, а убывает на промежутке $(-1, 1)$.

Промежуток убывания:

Как показано выше, функция убывает на промежутке $(-1, 1)$.

Шаг 3: Критические точки

Критические точки — это точки, где производная равна нулю или не существует. Мы уже нашли выражение для производной:

$$y'(x) = 3x^2 — 3$$

Приравняем её к нулю, чтобы найти критические точки:

$$3x^2 — 3 = 0$$

Решим это уравнение:

$$x^2 = 1$$ $$x = \pm 1$$

Таким образом, у нас есть две критические точки: $x = -1$ и $x = 1$.

Шаг 4: Анализируем максимум и минимум

Теперь нам нужно понять, где находятся максимумы и минимумы функции. Это делается с помощью анализа производной.

• Для $x = -1$: Производная меняет знак с положительного на отрицательное, что указывает на максимум.
• Для $x = 1$: Производная меняет знак с отрицательного на положительное, что указывает на минимум.

Таким образом, точка $x = -1$ — это точка максимума, а точка $x = 1$ — это точка минимума.

Шаг 5: Находим значения функции в этих точках

Теперь вычислим значения функции в критических точках, чтобы найти максимумы и минимумы:

Для $x = -1$:

$$y(-1) = (-1)^3 — 3(-1) + 2 = -1 + 3 + 2 = 4$$

Таким образом, в точке $x = -1$ максимальное значение функции $y = 4$.

Для $x = 1$:

$$y(1) = 1^3 — 3(1) + 2 = 1 — 3 + 2 = 0$$

Таким образом, в точке $x = 1$ минимальное значение функции $y = 0$.

Шаг 6: Координаты некоторых точек

Теперь вычислим значение функции в нескольких точках:

• Для $x = -2$:

$$y(-2) = (-2)^3 — 3(-2) + 2 = -8 + 6 + 2 = 0$$

• Для $x = 0$:

$$y(0) = (0)^3 — 3(0) + 2 = 2$$

• Для $x = 2$:

$$y(2) = (2)^3 — 3(2) + 2 = 8 — 6 + 2 = 4$$

Таким образом, таблица значений выглядит следующим образом:

Шаг 7: Касательная параллельна оси $Ox$

Если касательная к графику функции параллельна оси $Ox$, то производная в этой точке равна нулю. Мы уже нашли, что производная равна нулю в точках $x = -1$ и $x = 1$. Таким образом, касательная параллельна оси $Ox$ в точках $(-1; 4)$ и $(1; 0)$.