ГДЗ по Алгебре 10-11 Класс Номер 1531 Алимов — Подробные Ответы

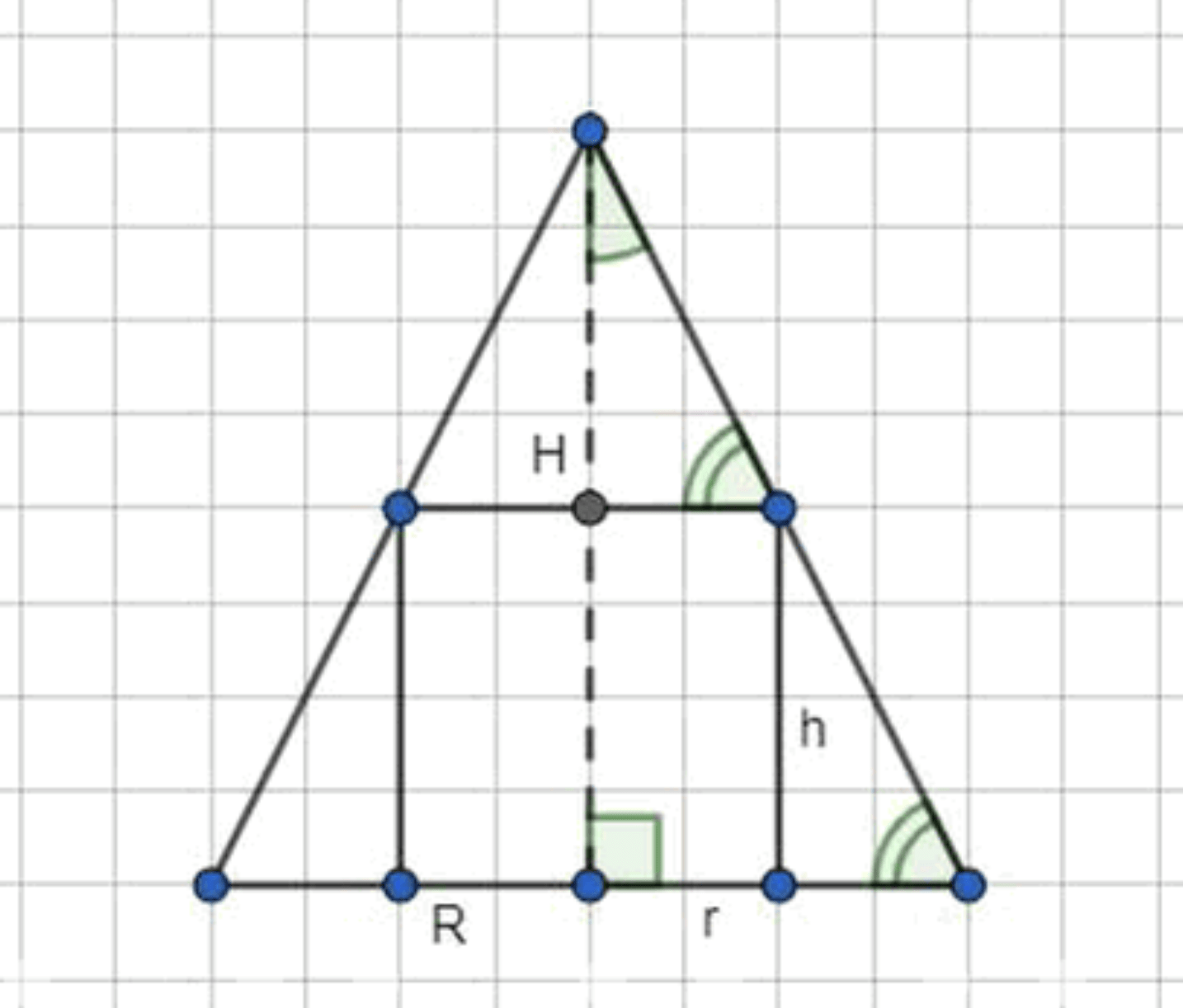
Из всех цилиндров, вписанных в конус с радиусом основания R и высотой Н, найти цилиндр наибольшего объёма.

Отобразим условие задачи:

Пусть $r$ и $h$ — радиус основания и высота цилиндра;

Радиус основания конуса равен $R$, а высота равна $H$, в него вписан цилиндр, значит:

$$\frac{h}{H} = \frac{(R — r)}{R};$$ $$h = \frac{H(R — r)}{R};$$

Объем цилиндра:

$$V(r) = \pi r^2 \cdot h = \pi r^2 \cdot \frac{H(R — r)}{R} = \frac{HR \pi r^2 — H \pi r^3}{R};$$

Производная функции:

$$V'(r) = \frac{H \pi}{R} \cdot (R(r^2)’ — (r^3)’) = \frac{H \pi}{R} \cdot (2Rr — 3r^2);$$

Промежуток возрастания:

$$2Rr — 3r^2 > 0;$$ $$r \cdot (2R — 3r) > 0;$$ $$r \cdot (3r — 2R) < 0;$$ $$0 < r < \frac{2R}{3};$$

Искомые значения:

$$r = \frac{2R}{3} \quad \text{— точка максимума};$$ $$h = \frac{H(R — \frac{2R}{3})}{R} = \frac{H \cdot \frac{R}{3}}{R} = \frac{H}{3};$$

Ответ: $r = \frac{2R}{3}; \quad h = \frac{H}{3}.$

Дано:

• $r$ — радиус основания цилиндра,
• $h$ — высота цилиндра,
• $R$ — радиус основания конуса,
• $H$ — высота конуса.

Цилиндр вписан в конус, что означает, что его основание лежит в основании конуса, а его боковая поверхность касается боковой поверхности конуса. Ваша задача — найти значения $r$ и $h$, при которых объем цилиндра максимален.

Шаг 1: Соотношение высоты цилиндра и конуса

Из условия задачи мы видим, что высоты цилиндра и конуса связаны между собой. Поскольку цилиндр вписан в конус, то отношение высоты цилиндра $h$ к высоте конуса $H$ равно отношению разности радиусов основания конуса и цилиндра $R — r$ к радиусу основания конуса $R$.

Это можно записать как:

$$\frac{h}{H} = \frac{R — r}{R}$$

Отсюда выражаем $h$:

$$h = \frac{H(R — r)}{R}$$

Шаг 2: Объем цилиндра

Теперь нам нужно найти объем цилиндра $V$. Формула объема цилиндра:

$$V = \pi r^2 h$$

Подставляем выражение для $h$ из предыдущего шага:

$$V(r) = \pi r^2 \cdot \frac{H(R — r)}{R}$$

Упростим это выражение:

$$V(r) = \frac{H \pi r^2 (R — r)}{R} = \frac{H \pi r^2 R — H \pi r^3}{R}$$

Шаг 3: Нахождение производной объема

Чтобы найти экстремумы объема (максимумы и минимумы), нам нужно вычислить производную объема $V'(r)$. Для этого применим правило дифференцирования к полученной функции объема.

$$V'(r) = \frac{d}{dr} \left( \frac{H \pi r^2 R — H \pi r^3}{R} \right)$$

Вынесем $\frac{H \pi}{R}$ за скобки:

$$V'(r) = \frac{H \pi}{R} \cdot \left( \frac{d}{dr} \left( r^2 R \right) — \frac{d}{dr} \left( r^3 \right) \right)$$

Теперь дифференцируем:

• $\frac{d}{dr} \left( r^2 R \right) = 2Rr$,
• $\frac{d}{dr} \left( r^3 \right) = 3r^2$.

Подставляем эти результаты в производную:

$$V'(r) = \frac{H \pi}{R} \cdot (2Rr — 3r^2)$$

Шаг 4: Нахождение критических точек

Для нахождения критических точек приравняем производную к нулю:

$$V'(r) = 0$$ $$\frac{H \pi}{R} \cdot (2Rr — 3r^2) = 0$$

Так как $\frac{H \pi}{R} \neq 0$, получаем:

$$2Rr — 3r^2 = 0$$

Вынесем $r$ за скобки:

$$r(2R — 3r) = 0$$

Решаем это уравнение:

$$r = 0 \quad \text{или} \quad 2R — 3r = 0$$

Из второго уравнения получаем:

$$r = \frac{2R}{3}$$

Таким образом, $r = 0$ и $r = \frac{2R}{3}$ — это критические точки.

Шаг 5: Анализ на промежутке возрастания и убывания

Чтобы понять, какая из критических точек соответствует максимуму объема, необходимо проанализировать знак производной на промежутке $0 < r < \frac{2R}{3}$ и за его пределами.

Для этого рассмотрим выражение $2Rr — 3r^2$. Разложим его:

$$2Rr — 3r^2 = r(2R — 3r)$$

Проанализируем знак:

• Для $0 < r < \frac{2R}{3}$, выражение $2R — 3r > 0$, следовательно, производная положительна, и объем растет.
• Для $r > \frac{2R}{3}$, выражение $2R — 3r < 0$, следовательно, производная отрицательна, и объем убывает.

Таким образом, объем максимален в точке $r = \frac{2R}{3}$.

Шаг 6: Нахождение высоты цилиндра

Теперь, когда мы знаем, что максимальный объем достигается при $r = \frac{2R}{3}$, можем найти высоту цилиндра $h$. Подставим это значение в выражение для $h$:

$$h = \frac{H(R — r)}{R}$$

Подставляем $r = \frac{2R}{3}$:

$$h = \frac{H \left( R — \frac{2R}{3} \right)}{R} = \frac{H \cdot \frac{R}{3}}{R} = \frac{H}{3}$$

Ответ:

Таким образом, максимальный объем цилиндра достигается при:

$$r = \frac{2R}{3}, \quad h = \frac{H}{3}$$

Ответ: $r = \frac{2R}{3}; \quad h = \frac{H}{3}$.