
Учебник «Алгебра» для 10-11 классов под авторством Алимова – это один из наиболее популярных и широко используемых учебных пособий для старшеклассников. Он заслужил признание как среди учителей, так и среди учеников благодаря своей структурированности, доступности изложения и качественной проработке материала.
ГДЗ по Алгебре 10-11 Класс Номер 1483 Алимов — Подробные Ответы
Построить график функции:
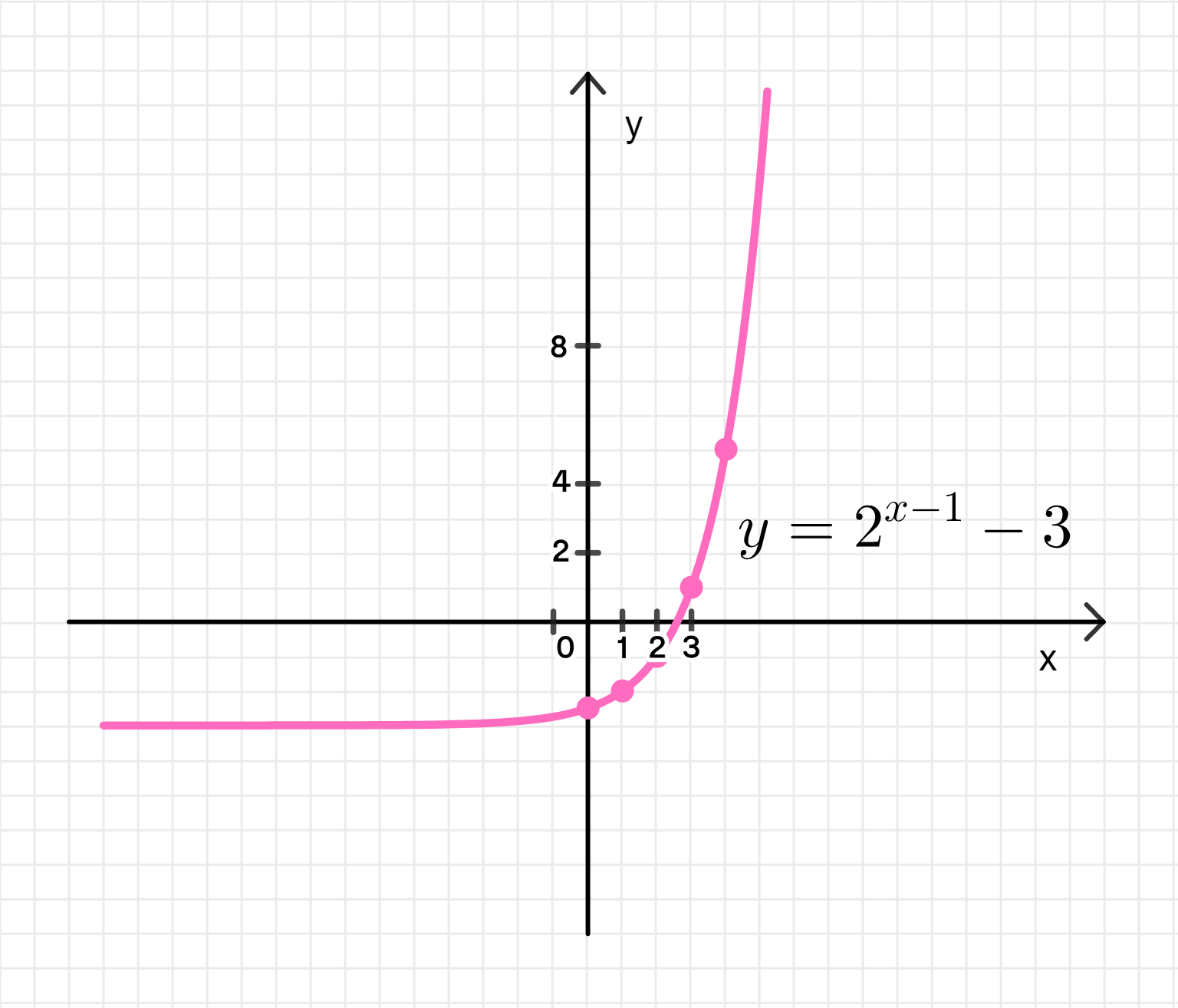
- у = 2(x-1) — 3;
- у = log2 (х + 2) + 3.
1)
Область определения функции:
Предел функции:
Производная функции:
Функция возрастает на всей числовой прямой;
Область значений функции:
Координаты некоторых точек:
| 0 | 1 | 2 | 3 | 4 | |
|---|---|---|---|---|---|
| -2.5 | -2 | -1 | 1 | 5 |
График функции:
2)
Область определения функции:
Предел функции:
Производная функции:
Промежуток возрастания:
Область значений функции:
Координаты некоторых точек:
| -1 | 0 | 2 | 6 | |
|---|---|---|---|---|
| 3 | 4 | 5 | 6 |
График функции:
1)
1.1: Область определения функции
Функция представляет собой экспоненциальную функцию , которая определена для всех . К этому прибавляется константа , которая также не влияет на область определения. Следовательно, область определения функции:
1.2: Предел функции при
Теперь вычислим предел функции при . Рассмотрим выражение:
При , экспоненциальная функция стремится к , поэтому:
Таким образом, предел функции при равен .
1.3: Производная функции
Найдем производную функции . Производная экспоненциальной функции по равна . Для функции производная будет такой же, с поправкой на множитель :
Так как для всех , и , производная функции всегда положительна:
Следовательно, функция возрастает на всей числовой прямой.
1.4: Область значений функции
Экспоненциальная функция принимает значения от до , а затем вычитается 3. Это означает, что функция будет принимать значения от до .
Таким образом, область значений функции:
1.5: Координаты точек пересечения с осями
Пересечение с осью (когда ):
Подставим в уравнение функции:
Таким образом, точка пересечения с осью — это .
Пересечение с осью (когда ):
Найдем, при каком функция пересекает ось , то есть решим уравнение :
Таким образом, точка пересечения с осью находится в точке , что примерно равно .
1.6: Координаты некоторых точек
Вычислим несколько значений функции для разных :
- :
- :
- :
- :
- :
Таблица координат некоторых точек:
1.7: График функции
2)
2.1: Область определения функции
Для того чтобы функция была определена, выражение под логарифмом должно быть больше нуля:
Таким образом, область определения функции:
2.2: Предел функции при
Найдем предел функции при :
Предел функции при равен .
2.3: Производная функции
Теперь найдем производную функции :
Поскольку на всей области определения, производная всегда положительна. Следовательно, функция возрастает на интервале .
2.4: Область значений функции
Логарифм с основанием 2 может принимать любые значения от до , а прибавленная константа сдвигает эту область на 3 единицы вверх. Таким образом, область значений функции:
2.5: Координаты точек пересечения с осями
Пересечение с осью (когда ):
Подставим в уравнение функции:
Таким образом, точка пересечения с осью — это .
2.6: Координаты некоторых точек
Вычислим значения функции для различных :
- :
- :
- :
- :
Таблица координат некоторых точек:
2.7: График функции


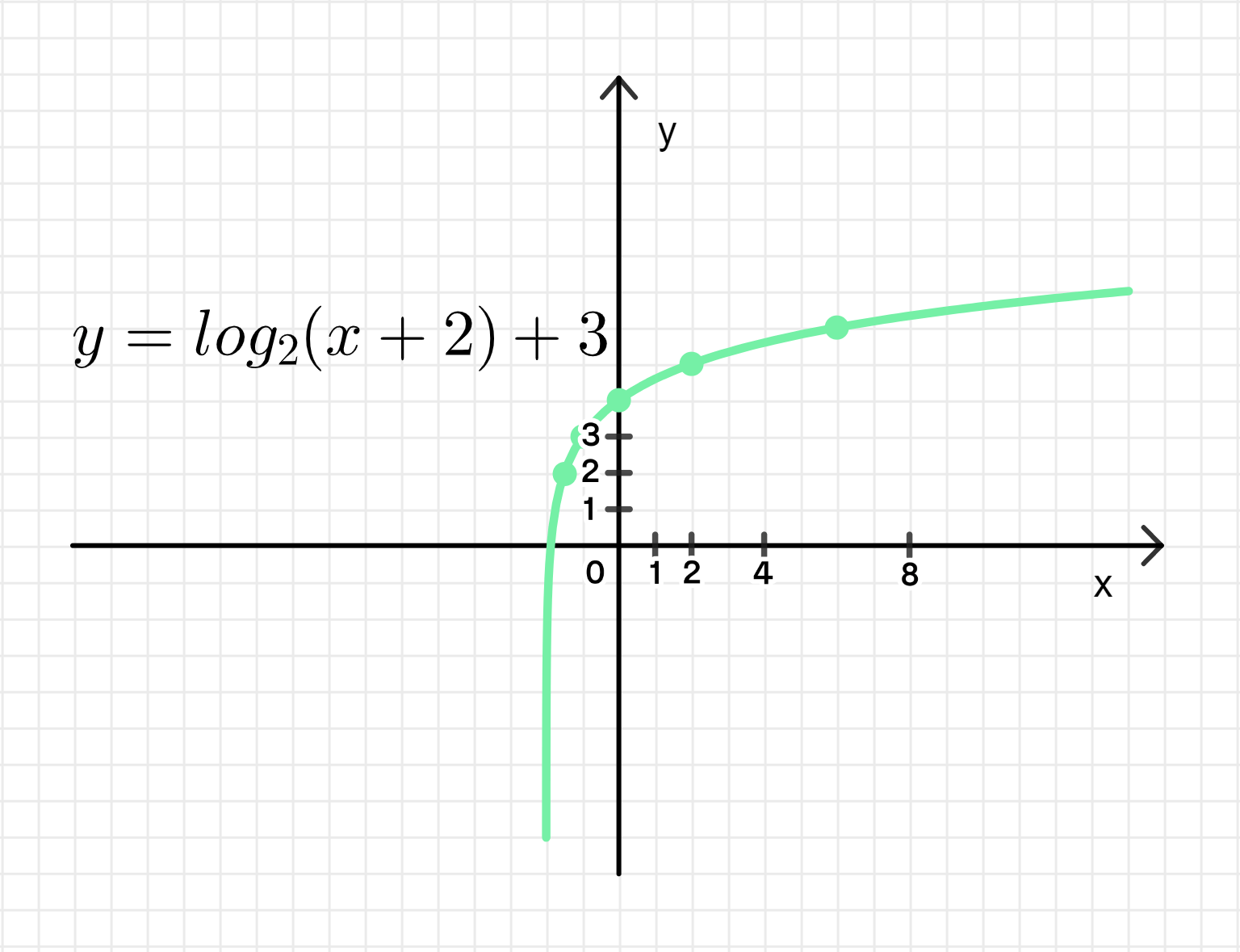

Оставь свой отзыв 💬
Комментариев пока нет, будьте первым!