
Учебник «Алгебра» для 10-11 классов под авторством Алимова – это один из наиболее популярных и широко используемых учебных пособий для старшеклассников. Он заслужил признание как среди учителей, так и среди учеников благодаря своей структурированности, доступности изложения и качественной проработке материала.
ГДЗ по Алгебре 10-11 Класс Номер 1482 Алимов — Подробные Ответы
Выяснить основные свойства функции и построить её график:
- у = Зх+1;
- у = log2 (х + 1);
- у = log1/3 (х- 1).
1)
- Функция ни четная, ни нечетная:
- Область определения функции:
- Предел функции:
- Производная функции:
- Функция возрастает на всей числовой прямой.
- Область значений функции:
- Пересечение с осью ():
- Координаты некоторых точек:
График функции:
2)
- Функция ни четная, ни нечетная:
- Область определения функции:
- Предел функции:
- Производная функции:
- Промежуток возрастания:
- Область значений функции:
- Пересечение с осью ():
- Координаты некоторых точек:
График функции:
3)
- Функция ни четная, ни нечетная:
- Область определения функции:
- Предел функции:
- Производная функции:
- Промежуток убывания:
- Область значений функции:
- Пересечение с осью ():
- Координаты некоторых точек:
График функции:
Даны три функции:
Мы проведем подробное исследование каждой из этих функций, а именно:
- Проверим, является ли функция четной или нечетной.
- Найдем область определения.
- Определим пределы функции при .
- Найдем производную функции.
- Проанализируем монотонность функции.
- Определим область значений.
- Найдем координаты точек пересечения с осями.
- Построим графики.
1)
1.1: Исследуем на четность и нечетность
Для проверки, является ли функция четной или нечетной, нужно исследовать, что происходит с функцией при замене на .
Функция четная, если , и нечетная, если .
Подставим в уравнение:
Это выражение не совпадает с , следовательно, функция ни четная, ни нечетная.
1.2: Область определения функции
Функция представляет собой сумму экспоненциальной функции и константы. Экспоненциальная функция определена для всех значений . Следовательно, область определения всей функции:
1.3: Предел функции при
Найдем предел функции при .
Таким образом, предел функции при равен .
1.4: Производная функции
Найдем производную функции .
Поскольку для всех , а , производная всегда положительна. Следовательно, функция возрастает на всей числовой прямой.
1.5: Область значений функции
Поскольку — это всегда положительная функция, а при , то функция будет всегда больше 1. Следовательно, область значений функции:
1.6: Пересечение с осью ()
Чтобы найти точку пересечения с осью , подставим в уравнение функции:
Точка пересечения с осью : .
1.7: Координаты некоторых точек
Найдем значения функции для различных :
- :
- :
- :
Таблица координат некоторых точек:
1.8: График функции
2)
2.1: Исследуем на четность и нечетность
Подставим в уравнение функции:
Это выражение не совпадает с , следовательно, функция ни четная, ни нечетная.
2.2: Область определения функции
Функция определена только для значений , то есть . Следовательно, область определения функции:
2.3: Предел функции при
Предел функции при не существует, так как логарифм стремится к при :
2.4: Производная функции
Найдем производную функции . Для этого используем правило дифференцирования логарифма с основанием 2:
Так как на области определения функции, производная всегда положительна. Это значит, что функция возрастает на всей своей области.
2.5: Область значений функции
Логарифм может принимать любые значения, начиная от и до , так как функция определена на интервале . Следовательно, область значений:
2.6: Пересечение с осью ()
Подставим в уравнение функции:
Точка пересечения с осью : .
2.7: Координаты некоторых точек
Найдем значения функции для различных :
- :
- :
- :
Таблица координат некоторых точек:
2.8: График функции
3)
3.1: Исследуем на четность и нечетность
Подставим в уравнение функции:
Это выражение не совпадает с , следовательно, функция ни четная, ни нечетная.
3.2: Область определения функции
Функция определена для значений , то есть . Следовательно, область определения функции:
3.3: Предел функции при
Предел функции при не существует, так как логарифм с основанием стремится к при :
3.4: Производная функции
Найдем производную функции . Используем правило дифференцирования логарифма с основанием :
Поскольку , производная всегда отрицательна, что означает, что функция убывает на всей области.
3.5: Область значений функции
Функция принимает все значения от до , так как логарифм с основанием может принимать любые значения. Следовательно, область значений функции:
3.6: Пересечение с осью ()
Найдем точку пересечения с осью , то есть решим уравнение :
Точка пересечения с осью : .
3.7: Координаты некоторых точек
Найдем значения функции для различных :
- :
- :
Таблица координат некоторых точек:
3.8: График функции


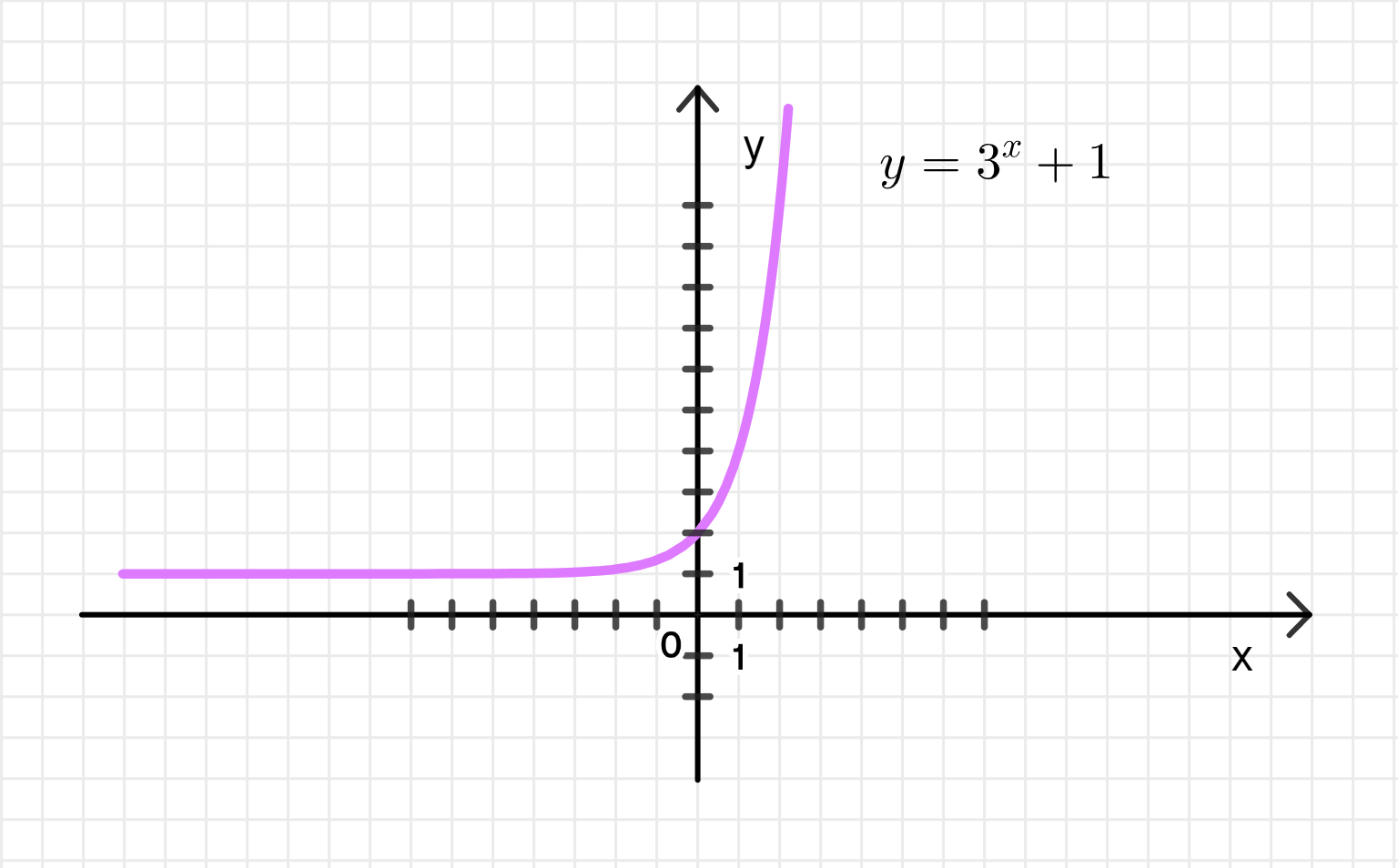
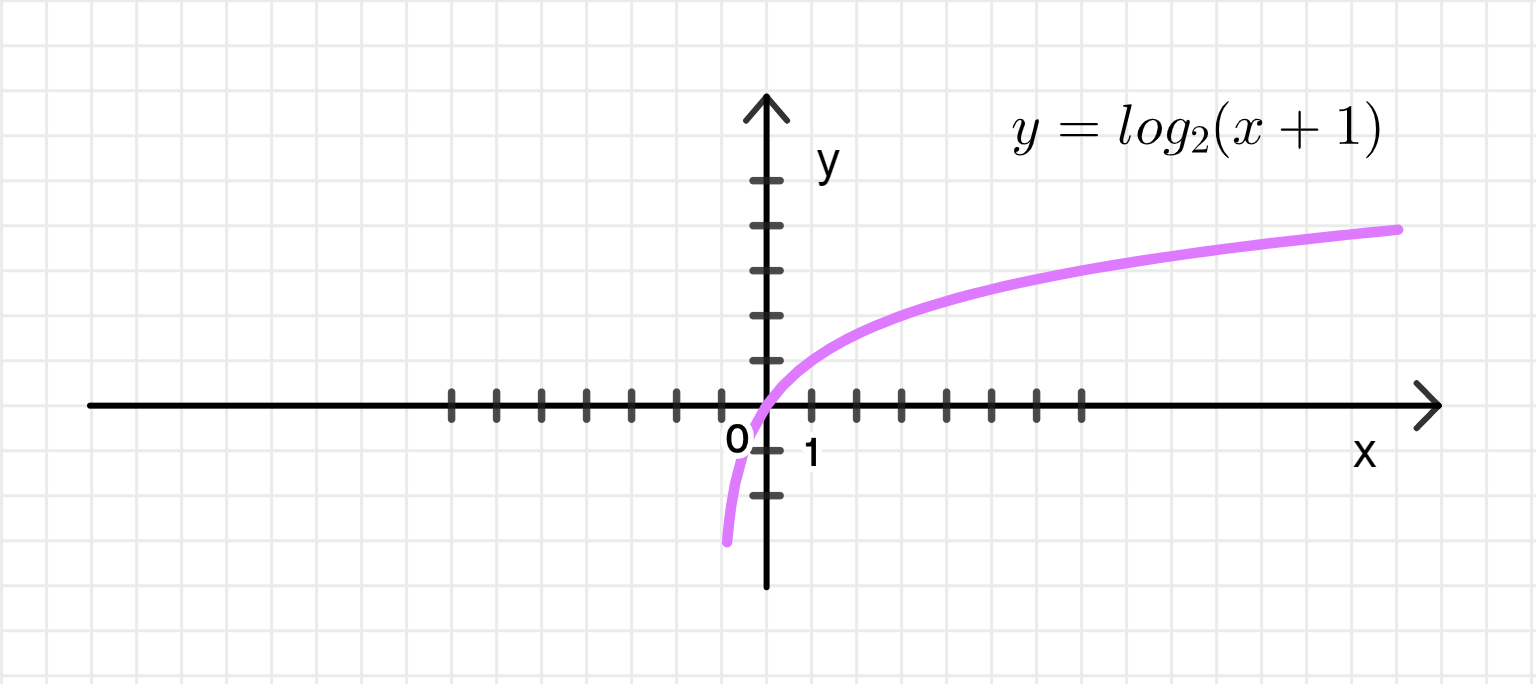
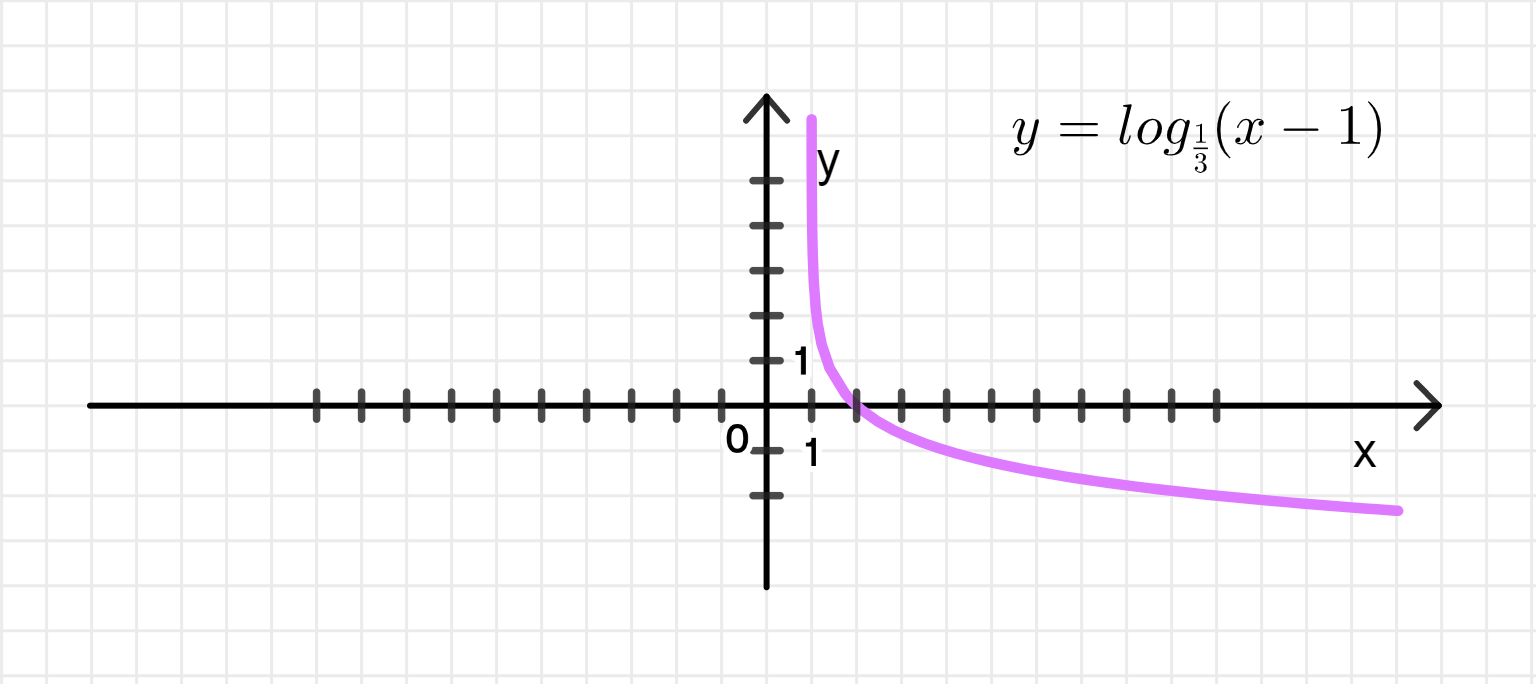

Оставь свой отзыв 💬
Комментариев пока нет, будьте первым!