ГДЗ по Алгебре 10-11 Класс Номер 1481 Алимов — Подробные Ответы

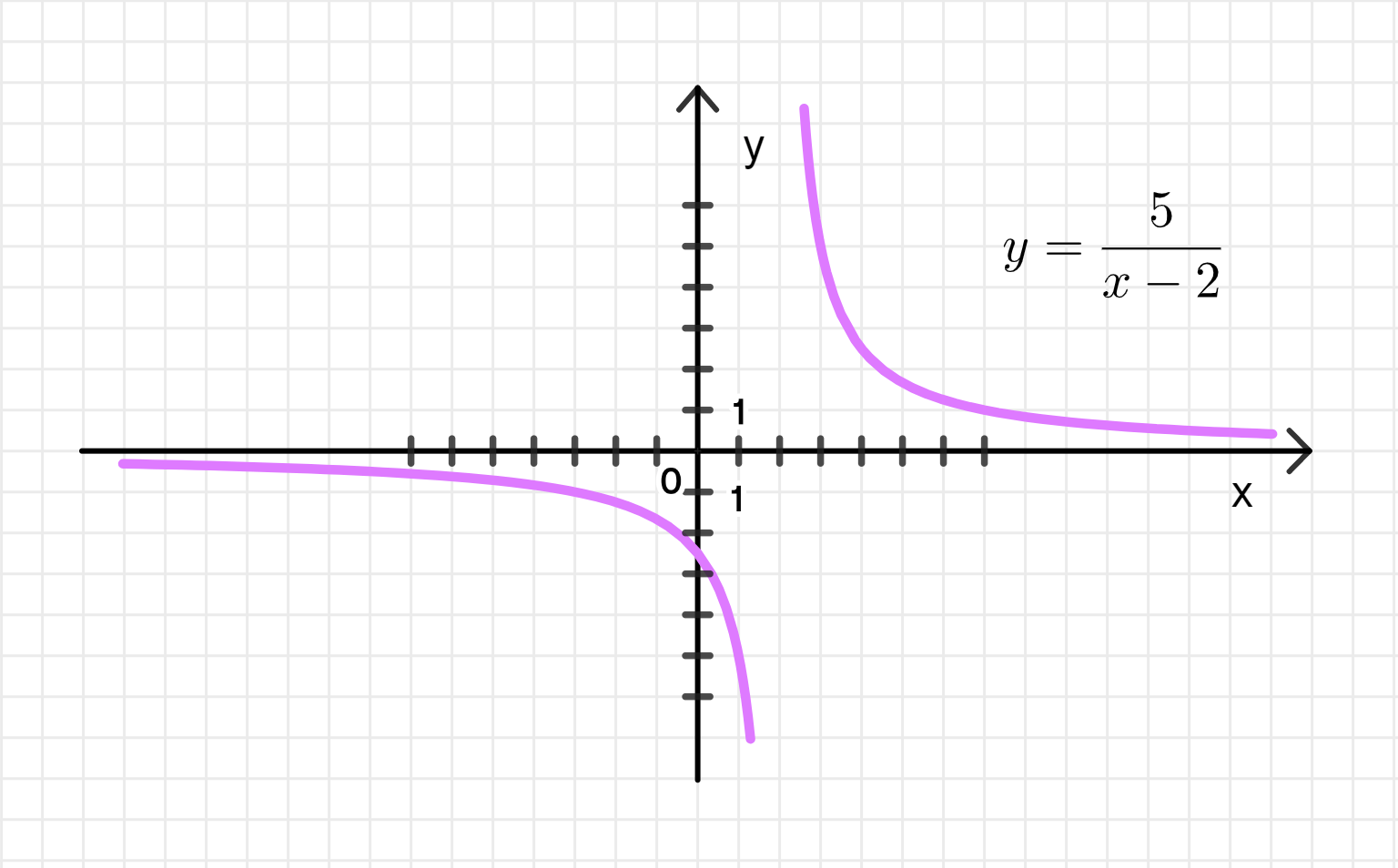
Построить график функции у = 5/(x-2). Доказать, что функция убывает на промежутках (-бесконечность; 2) и (2; +бесконечность). В какой точке график функции пересекает ось ординат?

Дана функция: $y = \frac{5}{x — 2}$;

Область определения функции:
$x — 2 \neq 0, \text{ отсюда } x \neq 2;$
$D(x) = (-\infty; 2) \cup (2; +\infty);$

Предел функции:
$\lim_{x \to \infty} \frac{5}{x — 2} = \lim_{x \to \infty} \frac{\frac{5}{x}}{1 — \frac{2}{x}} = \frac{0}{1 — 0} = \frac{0}{1} = 0;$

Производная функции:
$y'(x) = 5 \cdot (x — 2)^{-1′} = 5 \cdot (-1) \cdot (x — 2)^{-2} = -\frac{5}{(x — 2)^2} < 0;$
Производная меньше нуля, значит функция убывает на всей области определения, то есть на лучах $(-\infty; 2) \cup (2; +\infty)$, что и требовалось доказать.

Координаты некоторых точек:

График функции:

Дана функция:

$$y = \frac{5}{x — 2}$$

Необходимо:

1. Исследовать область определения функции.
2. Найти предел функции при $x \to \infty$.
3. Найти производную функции.
4. Проанализировать монотонность функции.
5. Найти координаты некоторых точек функции.
6. Построить график функции.

Шаг 1: Область определения функции

Для того чтобы функция была определена, знаменатель не должен быть равен нулю. Рассмотрим функцию:

$$y = \frac{5}{x — 2}$$

Для того чтобы знаменатель не был равен нулю, требуется:

$$x — 2 \neq 0 \quad \Rightarrow \quad x \neq 2$$

Следовательно, область определения функции $D(x)$ включает все значения $x$, кроме $x = 2$. Обозначим область определения следующим образом:

$$D(x) = (-\infty; 2) \cup (2; +\infty)$$

Это означает, что функция определена для всех значений $x$, за исключением $x = 2$, где она имеет разрыв.

Шаг 2: Предел функции при $x \to \infty$

Найдем предел функции $y = \frac{5}{x — 2}$ при $x \to \infty$. Рассмотрим выражение:

$$\lim_{x \to \infty} \frac{5}{x — 2}$$

Мы можем преобразовать дробь:

$$\frac{5}{x — 2} = \frac{\frac{5}{x}}{1 — \frac{2}{x}}$$

Теперь, при $x \to \infty$, обе части дроби стремятся к нулю:

$$\lim_{x \to \infty} \frac{5}{x} = 0, \quad \lim_{x \to \infty} \frac{2}{x} = 0$$

Таким образом:

$$\lim_{x \to \infty} \frac{5}{x — 2} = \frac{0}{1 — 0} = 0$$

Ответ: Предел функции при $x \to \infty$ равен 0.

Шаг 3: Производная функции

Теперь найдем производную функции $y = \frac{5}{x — 2}$. Для этого воспользуемся правилом дифференцирования функции вида $\frac{c}{x — a}$, где $c$ и $a$ — константы. Производная такой функции:

$$\frac{d}{dx} \left( \frac{c}{x — a} \right) = -\frac{c}{(x — a)^2}$$

В нашем случае $c = 5$ и $a = 2$, поэтому производная будет:

$$y'(x) = -\frac{5}{(x — 2)^2}$$

Это выражение говорит нам, что производная функции всегда отрицательна, так как квадрат любого числа всегда положителен. Следовательно, $y'(x) < 0$ для всех $x \in (-\infty; 2) \cup (2; +\infty)$.

Шаг 4: Монотонность функции

Мы уже выяснили, что производная функции $y'(x) = -\frac{5}{(x — 2)^2}$ всегда меньше нуля, что означает, что функция убывает на всей своей области определения.

Таким образом, функция убывает на каждом из интервалов области определения:

$$(-\infty; 2) \quad \text{и} \quad (2; +\infty)$$

Функция не может возрастать, так как производная всегда отрицательна.

Шаг 5: Координаты некоторых точек функции

Для того чтобы лучше понять поведение функции, найдем значения функции для некоторых точек из области определения.

Для $x = -3$:

$$y(-3) = \frac{5}{-3 — 2} = \frac{5}{-5} = -1$$

Для $x = 0$:

$$y(0) = \frac{5}{0 — 2} = \frac{5}{-2} = -2.5$$

Для $x = 1$:

$$y(1) = \frac{5}{1 — 2} = \frac{5}{-1} = -5$$

Для $x = 3$:

$$y(3) = \frac{5}{3 — 2} = \frac{5}{1} = 5$$

Для $x = 4$:

$$y(4) = \frac{5}{4 — 2} = \frac{5}{2} = 2.5$$

Для $x = 7$:

$$y(7) = \frac{5}{7 — 2} = \frac{5}{5} = 1$$

Таким образом, координаты некоторых точек функции:

$$\begin{array}{|c|c|c|c|c|c|c|} \hline x & -3 & 0 & 1 & 3 & 4 & 7 \\ \hline y & -1 & -2.5 & -5 & 5 & 2.5 & 1 \\ \hline \end{array}$$

Шаг 6: Графика функции

Ответ:

1. Область определения: $D(x) = (-\infty; 2) \cup (2; +\infty)$
2. Предел при $x \to \infty$: $0$
3. Производная: $y'(x) = -\frac{5}{(x — 2)^2}$
4. Монотонность: Функция убывает на интервалах $(-\infty; 2)$ и $(2; +\infty)$
5. Координаты некоторых точек:

   $$(-3, -1), (0, -2.5), (1, -5), (3, 5), (4, 2.5), (7, 1)$$

6. График функции — график убывает на обоих интервалах и имеет вертикальную асимптоту в $x = 2$ и горизонтальную асимптоту в $y = 0$.