ГДЗ по Алгебре 10-11 Класс Номер 1480 Алимов — Подробные Ответы

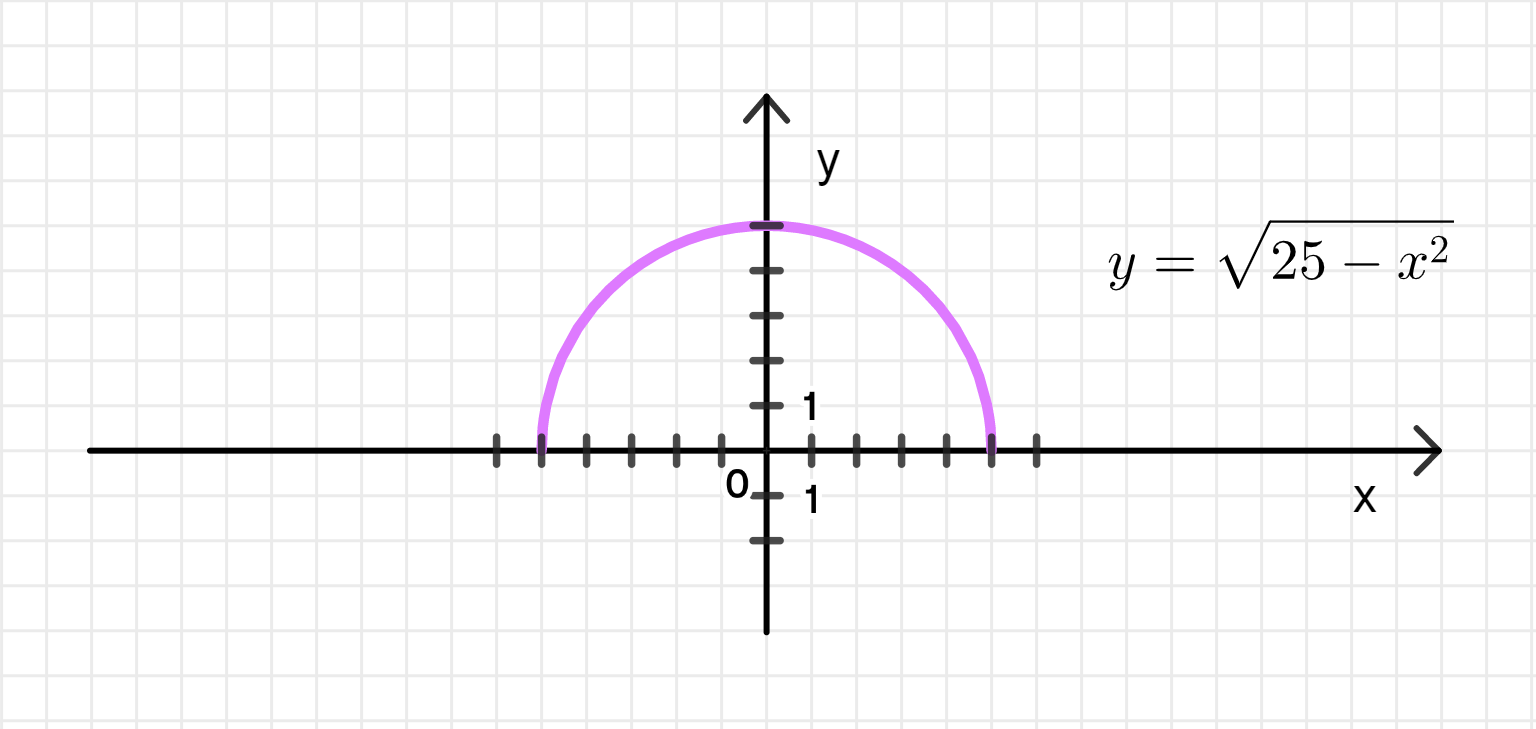
Построить график функции у = корень (25- х2). Указать по графику промежутки монотонности функции. Доказать, что гра фик данной функции симметричен относительно оси Оу.

Дана функция: $y = \sqrt{25 — x^2}$;

Исследуем функцию на четность:
$y(-x) = \sqrt{25 — (-x)^2} = \sqrt{25 — x^2} = y(x);$
Функция четная, что и требовалось доказать.

Область определения функции:
$25 — x^2 \geq 0;$
$x^2 \leq 25;$
$-5 \leq x \leq 5;$
$D(x) = [-5; 5];$

Пусть $u = 25 — x^2$, тогда $y(u) = \sqrt{u}$;
$y'(x) = (25 — x^2)’ \cdot (\sqrt{u})’ = (0 — 2x) \cdot \frac{1}{2\sqrt{y}} = \frac{-x}{\sqrt{26 — x^2}};$

Стационарные точки:
$x = 0;$
$y(0) = \sqrt{25 — 0^2} = \sqrt{25} = 5;$

Критические точки:
$y(\pm 5) = \sqrt{25 — (\pm 5)^2} = \sqrt{25 — 25} = 0;$

Координаты некоторых точек:

График функции:

Промежутки монотонности (по графику):

• Возрастает на $[-5; 0]$;
• Убывает на $[0; 5]$

Дана функция:

$$y = \sqrt{25 — x^2}$$

Необходимо исследовать функцию на четность, найти область определения, производную, стационарные и критические точки, а также промежутки монотонности.

Шаг 1: Исследуем функцию на четность

Функция $y(x) = \sqrt{25 — x^2}$ является четной, если выполняется равенство $y(-x) = y(x)$. Проверим это:

$$y(-x) = \sqrt{25 — (-x)^2} = \sqrt{25 — x^2} = y(x)$$

Таким образом, функция $y(x) = \sqrt{25 — x^2}$ является четной, что и требовалось доказать.

Шаг 2: Область определения функции

Функция $y = \sqrt{25 — x^2}$ имеет подкоренное выражение $25 — x^2$, которое должно быть неотрицательным, так как извлечение квадратного корня из отрицательного числа не определено в области действительных чисел.

Решим неравенство:

$$25 — x^2 \geq 0$$

Переносим $x^2$ на правую сторону:

$$x^2 \leq 25$$

Теперь берем квадратный корень с обеих сторон:

$$|x| \leq 5$$

Таким образом, область определения функции $D(x)$ равна:

$$D(x) = [-5; 5]$$

Шаг 3: Производная функции

Для нахождения производной функции используем правило дифференцирования сложной функции. Пусть:

$$u = 25 — x^2$$

Тогда функция примет вид:

$$y(u) = \sqrt{u}$$

Используя цепное правило, находим производную $y'(x)$. Сначала находим производную по $u$, затем по $x$:

$$y'(u) = \frac{1}{2\sqrt{u}}, \quad u'(x) = -2x$$

Теперь применяем цепное правило:

$$y'(x) = u'(x) \cdot y'(u) = (-2x) \cdot \frac{1}{2\sqrt{25 — x^2}} = \frac{-x}{\sqrt{25 — x^2}}$$

Таким образом, производная функции:

$$y'(x) = \frac{-x}{\sqrt{25 — x^2}}$$

Шаг 4: Стационарные точки

Стационарные точки — это точки, где производная функции равна нулю или не существует. Производная существует во всей области определения функции $D(x) = [-5; 5]$, так как знаменатель $\sqrt{25 — x^2}$ не равен нулю внутри области определения.

Найдем стационарные точки, при которых $y'(x) = 0$:

$$\frac{-x}{\sqrt{25 — x^2}} = 0$$

Это уравнение выполняется, когда числитель равен нулю, т.е. $x = 0$. Таким образом, $x = 0$ — это стационарная точка.

Теперь найдем значение функции в этой точке:

$$y(0) = \sqrt{25 — 0^2} = \sqrt{25} = 5$$

Таким образом, стационарная точка: $(0, 5)$.

Шаг 5: Критические точки

Критическими точками являются те, где производная не существует или равна нулю. Мы уже нашли, что производная равна нулю в точке $x = 0$.

Однако, также критическими точками будут точки, в которых функция $y(x) = \sqrt{25 — x^2}$ не существует. Эти точки происходят, когда выражение под квадратным корнем становится равным нулю, то есть когда $25 — x^2 = 0$.

Решаем это уравнение:

$$25 — x^2 = 0 \quad \Rightarrow \quad x^2 = 25 \quad \Rightarrow \quad x = \pm 5$$

Таким образом, критические точки: $x = 5$ и $x = -5$. Теперь найдем значения функции в этих точках:

$$y(5) = \sqrt{25 — 5^2} = \sqrt{25 — 25} = 0$$ $$y(-5) = \sqrt{25 — (-5)^2} = \sqrt{25 — 25} = 0$$

Таким образом, критические точки: $(5, 0)$ и $(-5, 0)$.

Шаг 6: Координаты некоторых точек

Для того чтобы более точно понять поведение функции, можно вычислить значения функции в некоторых точках:

• Для $x = 3$:

$$y(3) = \sqrt{25 — 3^2} = \sqrt{25 — 9} = \sqrt{16} = 4$$

• Для $x = 4$:

$$y(4) = \sqrt{25 — 4^2} = \sqrt{25 — 16} = \sqrt{9} = 3$$

Таблица с координатами некоторых точек:

$$\begin{array}{|c|c|c|} \hline x & 3 & 4 \\ \hline y & 4 & 3 \\ \hline \end{array}$$

Шаг 7: Промежутки монотонности

Теперь, используя производную, определим промежутки монотонности функции.

• Для $x \in [-5, 0]$, $y'(x) = \frac{-x}{\sqrt{25 — x^2}}$. На этом промежутке $x$ отрицательное, поэтому производная $y'(x) > 0$. Следовательно, функция возрастает на интервале $[-5; 0]$.
• Для $x \in [0, 5]$, $y'(x) = \frac{-x}{\sqrt{25 — x^2}}$. На этом промежутке $x$ положительное, поэтому производная $y'(x) < 0$. Следовательно, функция убывает на интервале $[0; 5]$.

Итак, функция:

• Возрастает на интервале $[-5; 0]$
• Убывает на интервале $[0; 5]$

Шаг 8: График функции

Ответ:

• Функция четная.
• Область определения: $D(x) = [-5; 5]$.
• Стационарная точка: $(0, 5)$.
• Критические точки: $(-5, 0)$ и $(5, 0)$.
• Промежутки монотонности:
  • Возрастает на $[-5; 0]$.
  • Убывает на $[0; 5]$.