
Учебник «Алгебра» для 10-11 классов под авторством Алимова – это один из наиболее популярных и широко используемых учебных пособий для старшеклассников. Он заслужил признание как среди учителей, так и среди учеников благодаря своей структурированности, доступности изложения и качественной проработке материала.
ГДЗ по Алгебре 10-11 Класс Номер 1479 Алимов — Подробные Ответы
Построить график функции у = ах2 + bх + с, если у (-2) = 15, у (3) = 0, у (0) = -3.
Дана функция: .
- Условие :
- Условие :
- Условие :
Подставим :
Теперь найдем :
- Подставим известные параметры , , :
Координаты вершины параболы:
Координаты некоторых точек:
График функции:
Дана квадратичная функция , где , , и — неизвестные коэффициенты. Необходимо найти параметры , , и с использованием заданных условий и затем построить график функции.
Шаг 1: Используем первое условие
Для нахождения значения подставляем в уравнение функции. При этом , и функция примет вид:
Это упрощается до:
Таким образом, .
Шаг 2: Используем второе условие
Теперь, когда мы знаем , подставим в уравнение функции. По условию, :
Подставляем :
Упростим это уравнение:
Теперь выразим через :
Таким образом, мы нашли зависимость .
Шаг 3: Используем третье условие
Теперь подставим в уравнение функции, по условию :
Подставляем и выражение для :
Раскроем скобки:
Упростим:
Переносим 5 на правую сторону:
Делим обе стороны на 10:
Теперь, когда мы нашли , подставим это значение в выражение для :
Шаг 4: Подставим найденные значения в уравнение
Теперь, когда мы нашли значения , и , можем подставить их в исходное уравнение функции:
Таким образом, уравнение функции имеет вид:
Шаг 5: Найдем координаты вершины параболы
Вершина параболы для квадратичной функции находится по формуле для абсциссы вершины:
Подставляем значения и :
Теперь найдем ординату вершины, подставив в уравнение функции:
Посчитаем каждый элемент:
Приведем все дроби к общему знаменателю:
Итак, координаты вершины параболы:
Шаг 6: Найдем координаты некоторых точек функции
Теперь найдем значения функции в нескольких точках для построения графика:
- Для :
- Для :
- Для :
- Для :
- Для :
- Для :
Таким образом, координаты точек для графика:
Шаг 7: Построение графика функции


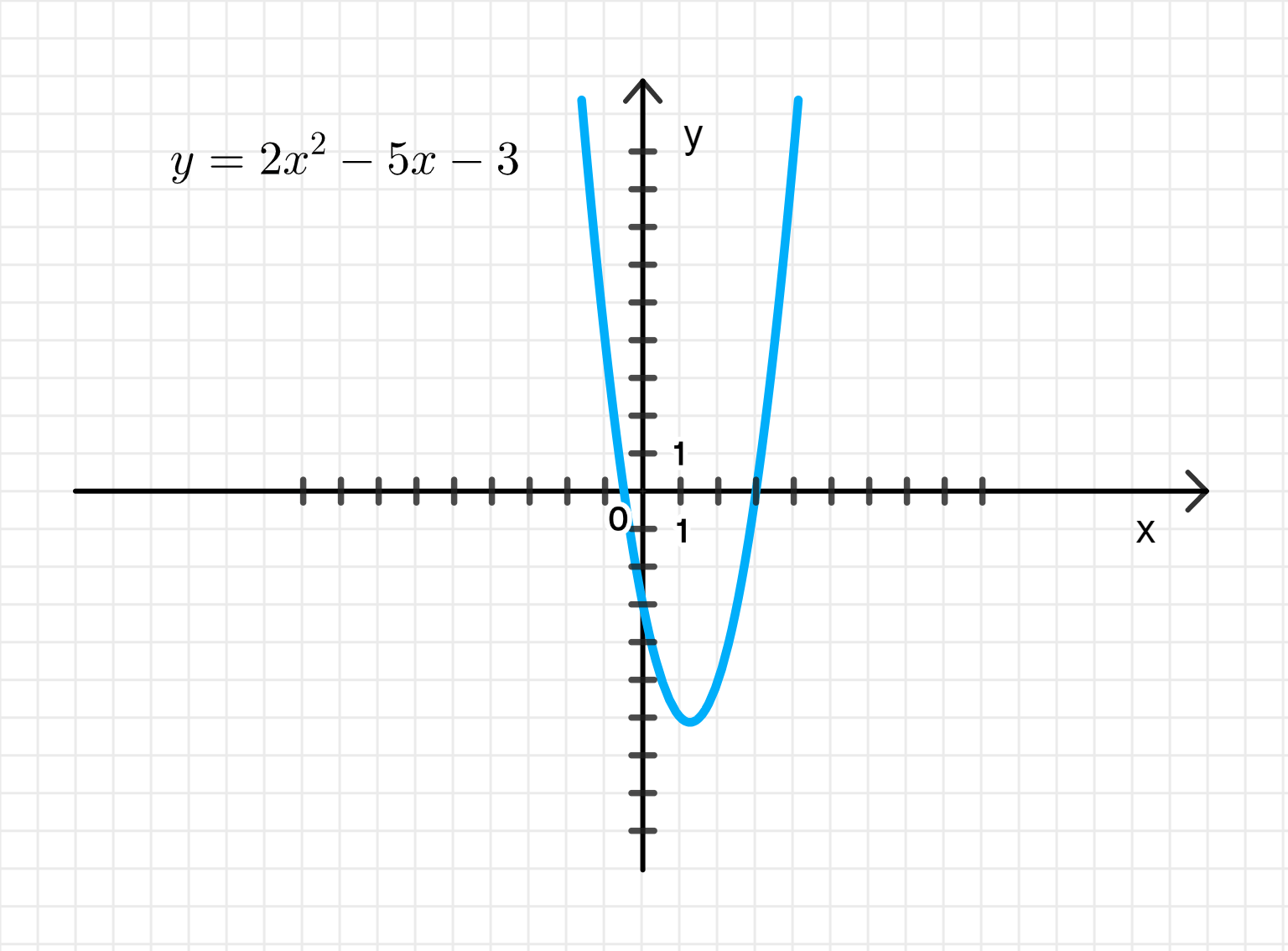

Оставь свой отзыв 💬
Комментариев пока нет, будьте первым!