ГДЗ по Алгебре 10-11 Класс Номер 1468 Алимов — Подробные Ответы

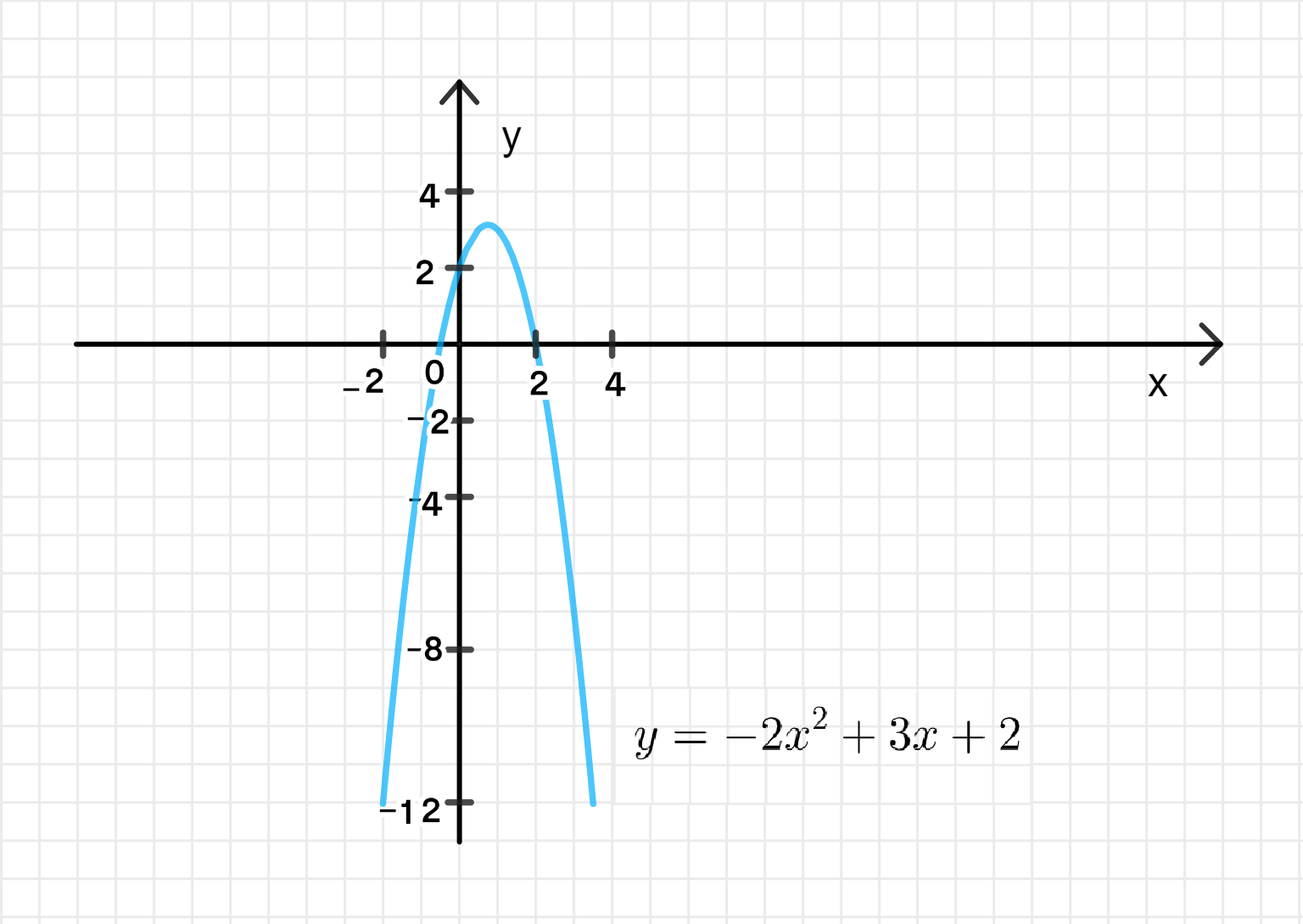
Дана функция у = -2х2 + Зх + 2.

1. Построить её график и найти значения х, при которых у (х) < 0.
2. Доказать, что функция убывает на отрезке [1; 2].
3. Найти значение х, при котором функция принимает наибольшее значение.
4. Найти значения х, при которых график данной функции лежит ниже графика функции у — Зх + 2.
5. Записать уравнения касательных к параболе у = -2х2 + Зх + 2 в точках с ординатой, равной 3.

Дана функция: $y = -2x^2 + 3x + 2$;

График функции:

Значения $x$, при которых $y(x) < 0$:

$$-2x^2 + 3x + 2 < 0;$$ $$2x^2 — 3x — 2 > 0;$$ $$D = 3^2 + 4 \cdot 2 \cdot 2 = 9 + 16 = 25, \text{ тогда: }$$ $$x_1 = \frac{3 — 5}{2 \cdot 2} = -\frac{1}{2} \quad \text{и} \quad x_2 = \frac{3 + 5}{2 \cdot 2} = 2;$$ $$\left( x + \frac{1}{2} \right)(x — 2) > 0;$$ $$x < -\frac{1}{2} \quad \text{и} \quad x > 2;$$

2) Докажем, что функция убывает на отрезке $[1; 2]$:

$$y'(x) = -2(x^2)’ + (3x + 2)’ = -2 \cdot 2x + 3 = 3 — 4x;$$

Промежуток убывания:

$$3 — 4x \leq 0;$$ $$4x \geq 3;$$ $$x \geq \frac{3}{4};$$

Функция убывает при $x \geq \frac{3}{4}$, что и требовалось доказать.

3) Наибольшее значение функции:

$$x = \frac{3}{4} — \text{точка максимума};$$ $$y\left( \frac{3}{4} \right) = -2 \cdot \frac{9}{16} + 3 \cdot \frac{3}{4} + 2 = -\frac{9}{8} + \frac{18}{8} + 2 = 1 \frac{1}{8} + 2 = 3 \frac{1}{8};$$

4) Значения $x$, при которых график данной функции лежит ниже графика функции $y = 3x + 2$:

$$-2x^2 + 3x + 2 < 3x + 2;$$ $$-2x^2 < 0;$$ $$x^2 > 0;$$ $$x \neq 0;$$

5) Уравнение касательной к данной функции в точках $y = 3$:

$$3 = -2x^2 + 3x + 2;$$ $$2x^2 — 3x + 1 = 0;$$ $$D = 3^2 — 4 \cdot 2 \cdot 2 = 9 — 8 = 1, \text{ тогда: }$$ $$x_1 = \frac{3 — 1}{2 \cdot 2} = \frac{1}{2} \quad \text{и} \quad x_2 = \frac{3 + 1}{2 \cdot 2} = 1;$$

Производная функции:

$$f'(x) = -2(x^2)’ + (3x + 2)’ = -2 \cdot 2x + 3 = 3 — 4x;$$

Уравнение первой касательной:

$$f’\left( \frac{1}{2} \right) = 3 — 4 \cdot \frac{1}{2} = 3 — 2 = 1;$$ $$y = 3 + 1 \left( x — \frac{1}{2} \right) = 3 + x — \frac{1}{2} = 2.5 + x;$$

Уравнение второй касательной:

$$f'(1) = 3 — 4 \cdot 1 = 3 — 4 = -1;$$ $$y = 3 — 1(x — 1) = 3 — x + 1 = 4 — x;$$

У нас дана квадратичная функция:

$$y = -2x^2 + 3x + 2$$

Необходимо рассмотреть несколько задач, связанных с графиком этой функции. Давайте разберём каждую задачу по порядку.

1) Найдём значения $x$, при которых $y(x) < 0$:

Необходимо решить неравенство:

$$-2x^2 + 3x + 2 < 0$$

Для удобства умножим обе части на -1 (учитывая, что при этом знак неравенства изменится):

$$2x^2 — 3x — 2 > 0$$

Теперь решим это неравенство, находя корни соответствующего уравнения:

$$2x^2 — 3x — 2 = 0$$

Для нахождения корней используем дискриминант:

$$D = (-3)^2 — 4 \cdot 2 \cdot (-2) = 9 + 16 = 25$$

Теперь найдём корни:

$$x_1 = \frac{-(-3) — \sqrt{25}}{2 \cdot 2} = \frac{3 — 5}{4} = -\frac{1}{2}$$ $$x_2 = \frac{-(-3) + \sqrt{25}}{2 \cdot 2} = \frac{3 + 5}{4} = 2$$

Таким образом, мы имеем два корня $x_1 = -\frac{1}{2}$ и $x_2 = 2$.

Теперь разложим исходное выражение на множители:

$$2x^2 — 3x — 2 = 2(x + \frac{1}{2})(x — 2)$$

Теперь решаем неравенство:

$$2(x + \frac{1}{2})(x — 2) > 0$$

Знаки произведения на интервалах:

1. $x < -\frac{1}{2}$ — оба множителя отрицательны, произведение положительное.
2. $-\frac{1}{2} < x < 2$ — один множитель положительный, другой отрицательный, произведение отрицательное.
3. $x > 2$ — оба множителя положительны, произведение положительное.

Значит, неравенство выполняется для:

$$x < -\frac{1}{2} \quad \text{или} \quad x > 2$$

Таким образом, значения $x$, при которых $y(x) < 0$, это $(-\infty, -\frac{1}{2}) \cup (2, \infty)$.

2) Докажем, что функция убывает на отрезке $[1; 2]$:

Найдем производную функции $y$:

$$y'(x) = -2(2x) + 3 = 3 — 4x$$

Теперь проверим, на каких интервалах производная отрицательна (функция убывает). Для этого решим неравенство:

$$3 — 4x \leq 0$$ $$4x \geq 3$$ $$x \geq \frac{3}{4}$$

Это означает, что функция убывает при $x \geq \frac{3}{4}$. Отрезок $[1; 2]$ полностью удовлетворяет этому условию, поскольку $1 \geq \frac{3}{4}$, и на данном отрезке функция действительно убывает.

Таким образом, функция убывает на отрезке $[1; 2]$, что и требовалось доказать.

3) Наибольшее значение функции:

Функция $y = -2x^2 + 3x + 2$ — это парабола, открытая вниз (так как коэффициент при $x^2$ отрицателен). Наибольшее значение она принимает в вершине параболы. Абсцисса вершины для квадратичной функции $ax^2 + bx + c$ находится по формуле:

$$x_{\text{max}} = \frac{-b}{2a}$$

Для нашей функции $a = -2$, $b = 3$, следовательно:

$$x_{\text{max}} = \frac{-3}{2 \cdot (-2)} = \frac{3}{4}$$

Теперь найдём значение функции в точке $x = \frac{3}{4}$:

$$y\left( \frac{3}{4} \right) = -2 \cdot \left( \frac{3}{4} \right)^2 + 3 \cdot \frac{3}{4} + 2 = -2 \cdot \frac{9}{16} + \frac{9}{4} + 2$$

Приведем к общему знаменателю:

$$y\left( \frac{3}{4} \right) = -\frac{18}{16} + \frac{36}{16} + \frac{32}{16} = \frac{18}{16} = 1 \frac{1}{8}$$

Таким образом, наибольшее значение функции равно $3 \frac{1}{8}$.

4) Значения $x$, при которых график функции лежит ниже графика функции $y = 3x + 2$:

Необходимо решить неравенство:

$$-2x^2 + 3x + 2 < 3x + 2$$

Упростим его:

$$-2x^2 < 0$$ $$x^2 > 0$$

Это неравенство выполняется при всех $x \neq 0$, так как квадрат любого числа (кроме нуля) больше нуля.

Ответ: график функции $y = -2x^2 + 3x + 2$ лежит ниже графика функции $y = 3x + 2$ для всех $x \neq 0$.

5) Уравнение касательной к функции в точках $y = 3$:

Для нахождения касательной, нужно решить уравнение:

$$3 = -2x^2 + 3x + 2$$

Переносим все на одну сторону:

$$2x^2 — 3x + 1 = 0$$

Находим дискриминант:

$$D = (-3)^2 — 4 \cdot 2 \cdot 1 = 9 — 8 = 1$$

Теперь находим корни:

$$x_1 = \frac{3 — 1}{2 \cdot 2} = \frac{1}{2}, \quad x_2 = \frac{3 + 1}{2 \cdot 2} = 1$$

Производная функции $y'(x) = 3 — 4x$. Теперь находим значения производной в точках касания.

Для $x_1 = \frac{1}{2}$:

$$y’\left( \frac{1}{2} \right) = 3 — 4 \cdot \frac{1}{2} = 3 — 2 = 1$$

Уравнение касательной в точке $x = \frac{1}{2}$ имеет вид:

$$y — 3 = 1 \cdot (x — \frac{1}{2}) \quad \Rightarrow \quad y = 3 + (x — \frac{1}{2}) = 3 + x — \frac{1}{2} = 2.5 + x$$

Для $x_2 = 1$:

$$y’\left( 1 \right) = 3 — 4 \cdot 1 = 3 — 4 = -1$$

Уравнение касательной в точке $x = 1$ имеет вид:

$$y — 3 = -1 \cdot (x — 1) \quad \Rightarrow \quad y = 3 — (x — 1) = 3 — x + 1 = 4 — x$$

Таким образом, уравнения касательных:

1. $y = 2.5 + x$ при $x = \frac{1}{2}$,
2. $y = 4 — x$ при $x = 1$.