ГДЗ по Алгебре 10-11 Класс Номер 1467 Алимов — Подробные Ответы

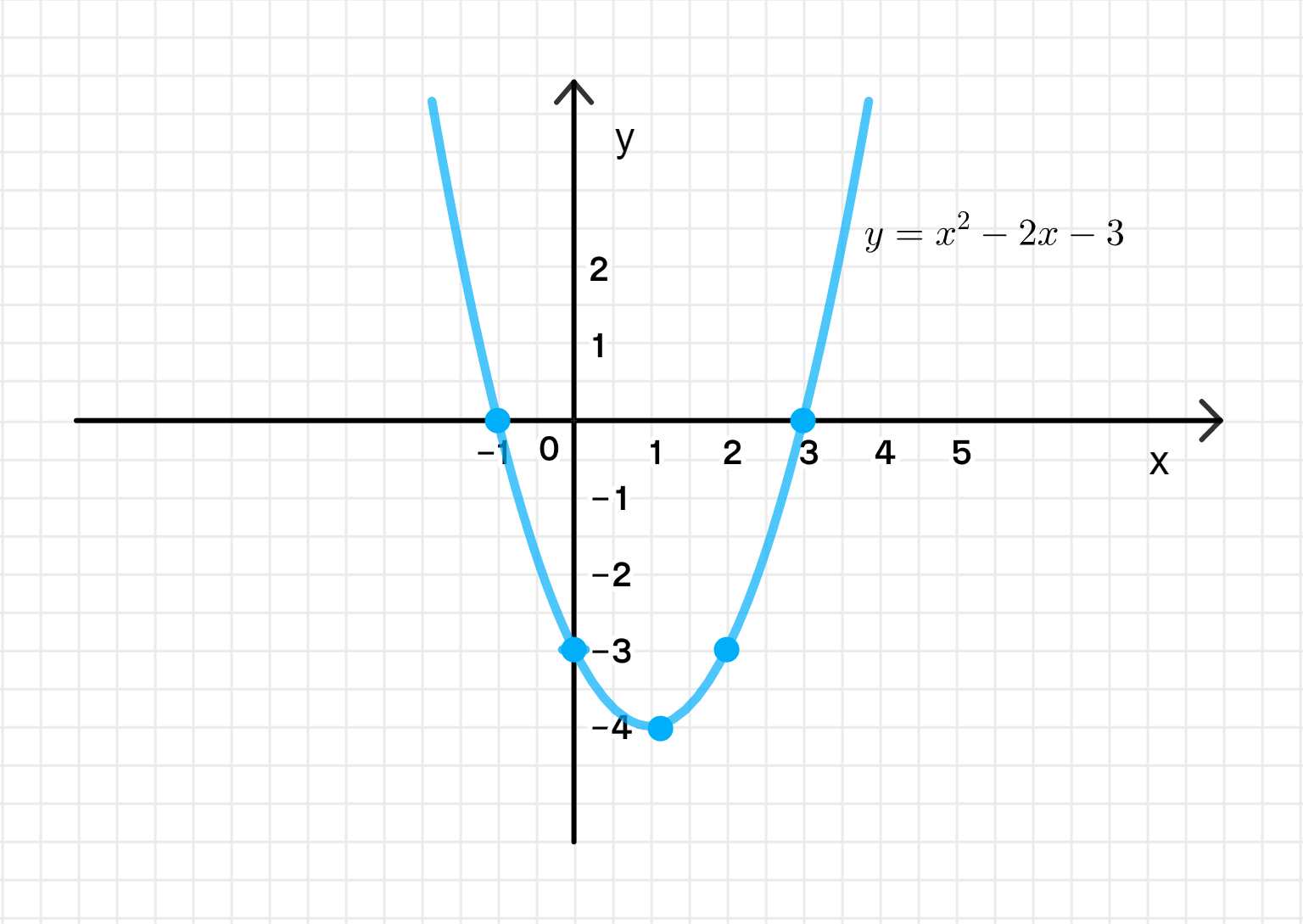
Дана функция у = х2 — 2х — 3.

1. Построить её график и найти значения х, при которых У (x) < 0.
2. Доказать, что функция возрастает на отрезке [1; 4].
3. Найти значение х, при котором функция принимает наименьшее значение.
4. Найти значения х, при которых график функции у = х2 — 2х — 3 лежит выше графика функции у = —2х + 1.
5. Записать уравнение касательной к параболе у = х2 — 2х — 3 в точке с абсциссой, равной 2.

Дана функция: $y = x^2 — 2x — 3$;

График функции:

Значения $x$, при которых $y(x) < 0$:

$$x^2 — 2x — 3 < 0;$$ $$D = 2^2 + 4 \cdot 3 = 4 + 12 = 16, \text{ тогда:}$$ $$x_1 = \frac{2 — 4}{2} = -1 \quad \text{и} \quad x_2 = \frac{2 + 4}{2} = 3;$$ $$(x + 1)(x — 3) < 0;$$ $$-1 < x < 3;$$

2) Докажем, что функция возрастает на отрезке $[1; 4]$:

$$y'(x) = (x^2)’ — (2x + 3)’ = 2x — 2;$$

Промежуток возрастания:

$$2x — 2 \geq 0;$$ $$x — 1 \geq 0;$$ $$x \geq 1;$$

Функция возрастает при $x \geq 1$, что и требовалось доказать.

3) Наименьшее значение функции:

$$x = 1 \text{ — точка минимума};$$ $$y(1) = 1^2 — 2 \cdot 1 — 3 = 1 — 2 — 3 = -4;$$

4) Значения $x$, при которых график данной функции лежит выше графика функции $y = -2x + 1$:

$$x^2 — 2x — 3 > -2x + 1;$$ $$x^2 > 4;$$ $$x < -2 \quad \text{и} \quad x > 2;$$

5) Уравнение касательной к данной функции в точке $x = 2$:

$$f'(x) = (x^2)’ — (2x + 3)’ = 2x — 2;$$ $$f'(2) = 2 \cdot 2 — 2 = 4 — 2 = 2;$$ $$f(2) = 2^2 — 2 \cdot 2 — 3 = 4 — 4 — 3 = -3;$$ $$y = -3 + 2(x — 2) = -3 + 2x — 4 = 2x — 7;$$

Дана функция:

$$y = x^2 — 2x — 3$$

График функции:

1) Найдем значения $x$, при которых $y(x) < 0$.

Функция дана как квадратичная:

$$y = x^2 — 2x — 3$$

Нам нужно решить неравенство:

$$x^2 — 2x — 3 < 0$$

Для этого сначала найдем корни квадратного уравнения $x^2 — 2x — 3 = 0$ с помощью дискриминанта.

Шаг 1.1: Находим дискриминант $D$.

Формула для дискриминанта для квадратного уравнения $ax^2 + bx + c = 0$ следующая:

$$D = b^2 — 4ac$$

В нашем случае:
$a = 1$, $b = -2$, $c = -3$.

Подставляем в формулу для дискриминанта:

$$D = (-2)^2 — 4 \cdot 1 \cdot (-3) = 4 + 12 = 16$$

Шаг 1.2: Находим корни уравнения.

Корни квадратного уравнения находятся по формулам:

$$x_1 = \frac{-b — \sqrt{D}}{2a}, \quad x_2 = \frac{-b + \sqrt{D}}{2a}$$

Подставляем значения $a = 1$, $b = -2$, $D = 16$:

$$x_1 = \frac{-(-2) — \sqrt{16}}{2 \cdot 1} = \frac{2 — 4}{2} = \frac{-2}{2} = -1$$ $$x_2 = \frac{-(-2) + \sqrt{16}}{2 \cdot 1} = \frac{2 + 4}{2} = \frac{6}{2} = 3$$

Итак, корни уравнения $x_1 = -1$ и $x_2 = 3$.

Шаг 1.3: Разбираем знак выражения $(x + 1)(x — 3)$.

Из условий задачи нам нужно решить неравенство:

$$(x + 1)(x — 3) < 0$$

Для этого определяем, на каких интервалах произведение этих множителей будет меньше нуля. Это делаем через исследование знаков на интервалах, которые определяются корнями уравнения. У нас есть три интервала:

• $x < -1$
• $-1 < x < 3$
• $x > 3$

1. Интервал $x < -1$:
   Для $x = -2$, $(x + 1) = -1$, $(x — 3) = -5$, произведение будет положительным, т.е. $(+)$.
2. Интервал $-1 < x < 3$:
   Для $x = 0$, $(x + 1) = 1$, $(x — 3) = -3$, произведение будет отрицательным, т.е. $(-)$.
3. Интервал $x > 3$:
   Для $x = 4$, $(x + 1) = 5$, $(x — 3) = 1$, произведение будет положительным, т.е. $(+)$.

Таким образом, неравенство $(x + 1)(x — 3) < 0$ выполняется на интервале:

$$-1 < x < 3$$

Итак, значения $x$, при которых $y(x) < 0$, это:

$$-1 < x < 3$$

2) Докажем, что функция возрастает на отрезке $[1; 4]$.

Для этого нужно найти производную функции и проанализировать её знак на заданном интервале.

Шаг 2.1: Находим производную функции.

Для функции $y = x^2 — 2x — 3$ находим производную по стандартным правилам дифференцирования:

$$y'(x) = \frac{d}{dx}(x^2) — \frac{d}{dx}(2x) — \frac{d}{dx}(3) = 2x — 2$$

Шаг 2.2: Анализируем знак производной на интервале $[1; 4]$.

Нам нужно проверить, на каком интервале производная $y'(x) = 2x — 2$ больше нуля.

Решаем неравенство:

$$2x — 2 \geq 0$$

Приводим его к виду:

$$x \geq 1$$

Таким образом, производная функции $y'(x)$ положительна при $x \geq 1$, что означает, что функция возрастает на интервале $[1; 4]$.

Заключение: Функция возрастает на отрезке $[1; 4]$.

3) Найдем наименьшее значение функции.

Мы знаем, что парабола $y = x^2 — 2x — 3$ имеет минимум, так как коэффициент перед $x^2$ положительный. Минимум функции будет в вершине параболы.

Шаг 3.1: Находим координаты вершины параболы.

Формула для абсциссы вершины параболы $y = ax^2 + bx + c$:

$$x_{\text{верш}} = \frac{-b}{2a}$$

Для нашей функции $a = 1$, $b = -2$:

$$x_{\text{верш}} = \frac{-(-2)}{2 \cdot 1} = \frac{2}{2} = 1$$

Шаг 3.2: Находим значение функции в точке минимума.

Подставляем $x = 1$ в исходную функцию:

$$y(1) = 1^2 — 2 \cdot 1 — 3 = 1 — 2 — 3 = -4$$

Итак, наименьшее значение функции равно $-4$, и оно достигается в точке $x = 1$.

4) Найдем значения $x$, при которых график данной функции лежит выше графика функции $y = -2x + 1$.

Для этого решим неравенство:

$$x^2 — 2x — 3 > -2x + 1$$

Шаг 4.1: Переносим все в одну сторону:

$$x^2 — 2x — 3 + 2x — 1 > 0$$

Упрощаем:

$$x^2 — 4 > 0$$

Шаг 4.2: Решаем неравенство:

$$x^2 > 4$$

Из этого неравенства получаем:

$$x < -2 \quad \text{или} \quad x > 2$$

Итак, график функции $y = x^2 — 2x — 3$ лежит выше графика функции $y = -2x + 1$, когда:

$$x < -2 \quad \text{или} \quad x > 2$$

5) Найдем уравнение касательной к данной функции в точке $x = 2$.

Шаг 5.1: Находим производную функции.

Мы уже знаем, что:

$$y'(x) = 2x — 2$$

Шаг 5.2: Находим угловой коэффициент касательной.

Подставляем $x = 2$ в производную:

$$y'(2) = 2 \cdot 2 — 2 = 4 — 2 = 2$$

Угловой коэффициент касательной в точке $x = 2$ равен 2.

Шаг 5.3: Находим координаты точки касания.

Подставляем $x = 2$ в исходную функцию:

$$y(2) = 2^2 — 2 \cdot 2 — 3 = 4 — 4 — 3 = -3$$

Таким образом, точка касания имеет координаты $(2, -3)$.

Шаг 5.4: Составляем уравнение касательной.

Уравнение касательной имеет вид:

$$y — y_1 = m(x — x_1)$$

где $m$ — угловой коэффициент, а $(x_1, y_1)$ — точка касания.

Подставляем $m = 2$, $x_1 = 2$, $y_1 = -3$:

$$y — (-3) = 2(x — 2)$$

Упрощаем:

$$y + 3 = 2(x — 2)$$ $$y + 3 = 2x — 4$$ $$y = 2x — 7$$

Итак, уравнение касательной:

$$y = 2x — 7$$