
Учебник «Алгебра» для 10-11 классов под авторством Алимова – это один из наиболее популярных и широко используемых учебных пособий для старшеклассников. Он заслужил признание как среди учителей, так и среди учеников благодаря своей структурированности, доступности изложения и качественной проработке материала.
ГДЗ по Алгебре 10-11 Класс Номер 1466 Алимов — Подробные Ответы
Построить график функции:
- у = 2- |х|;
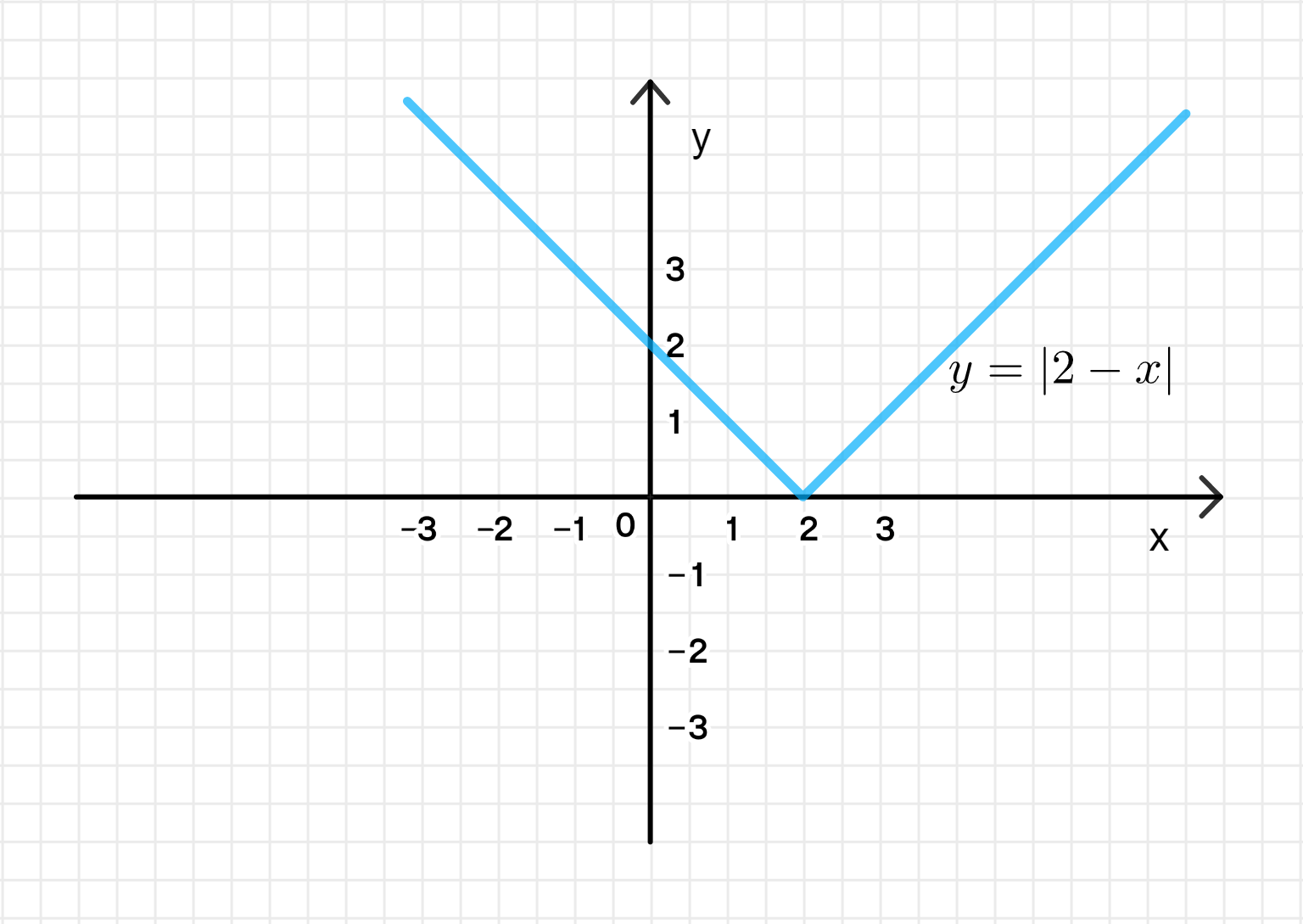
- у = |2 — х|;
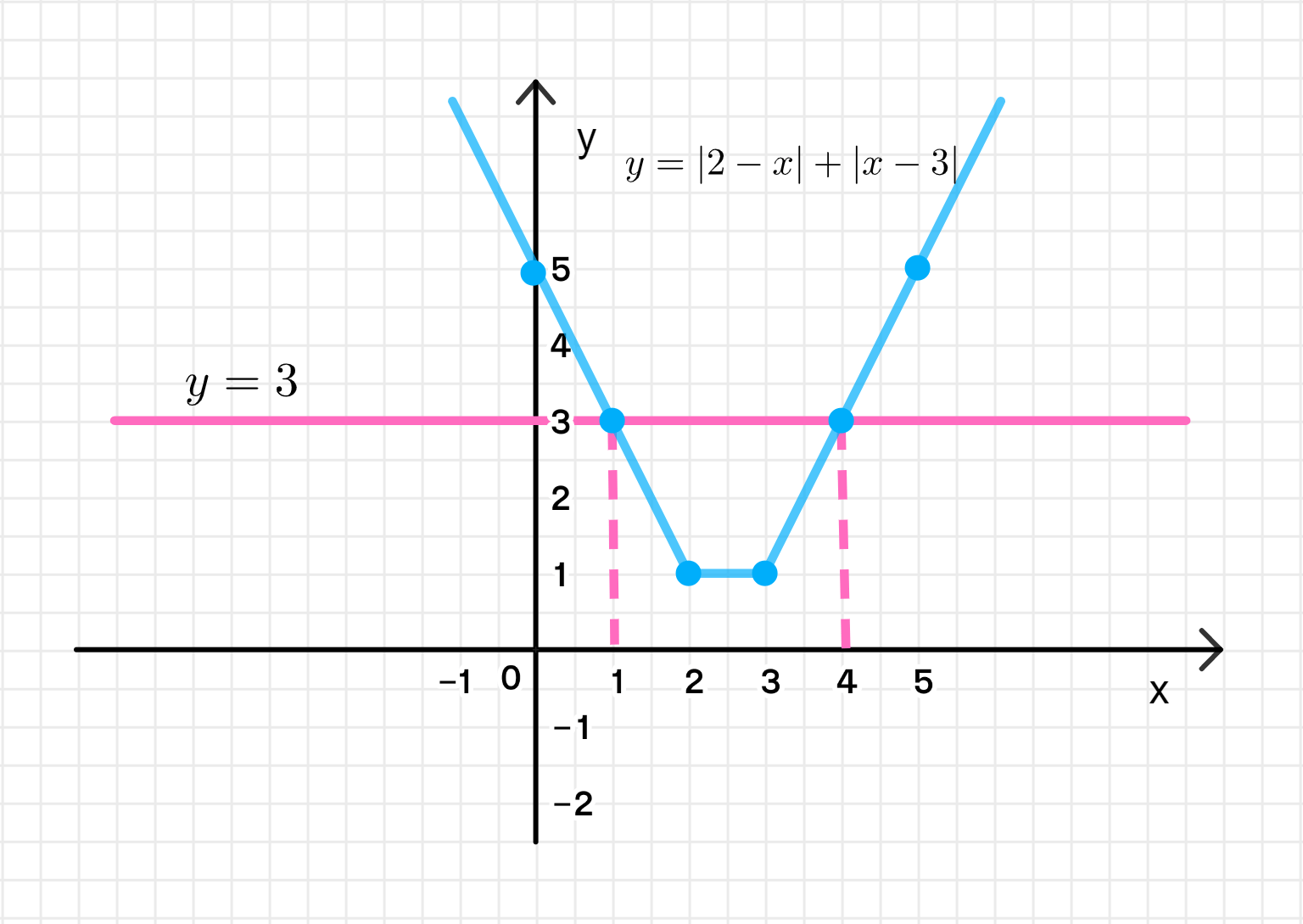
- у = |2 — х| + |х — 3|.
1)
- Координаты точки излома:
- Координаты некоторых точек:
- Точки пересечения с прямой :
- График функции:
- Ответ: не пересекает.
2)
- Координаты точки излома:
- Координаты некоторых точек:
- Точки пересечения с прямой :
- График функции:
- Ответ: ; .
3)
- Координаты первой точки излома:
- Координаты второй точки излома:
- Координаты некоторых точек:
- Точки пересечения с прямой :
- Если , тогда:
- Если , тогда:
- Если , тогда:
- Если , тогда:
- График функции
- Ответ: ; .
Необходимо решить задачу для трёх различных функций и найти их точки пересечения с прямой .
1) Функция
Шаг 1: Координаты точки излома
Функция имеет точку излома в точке , так как абсолютное значение меняет свой вид в этой точке.
Чтобы найти точку излома, при :
Таким образом, координаты точки излома:
Шаг 2: Координаты некоторых точек
Для других значений , например, и :
Получаем таблицу координат:
Шаг 3: Точки пересечения с прямой
Теперь решим уравнение для поиска точек пересечения с прямой :
Так как модуль числа всегда неотрицателен, а невозможно, то корней нет.
Ответ: Функция не пересекает прямую .
График функции:
График функции представляет собой букву «V», направленную вниз, с вершиной в точке .
Ответ: не пересекает.
2) Функция
Шаг 1: Координаты точки излома
Точка излома происходит, когда выражение внутри модуля равно нулю:
При :
Таким образом, координаты точки излома:
Шаг 2: Координаты некоторых точек
Для значений и :
Получаем таблицу координат:
Шаг 3: Точки пересечения с прямой
Решим уравнение для нахождения точек пересечения с прямой :
Модуль даёт два возможных случая:
Таким образом, точки пересечения:
Ответ: ;
График функции:
График функции представляет собой букву «V» с вершиной в точке , где линия наклоняется вверх.
3) Функция
Шаг 1: Координаты точек излома
Функция содержит два модуля, поэтому необходимо найти две точки излома:
При :
При :
Таким образом, координаты точек излома:
Шаг 2: Координаты некоторых точек
Для значений и :
Получаем таблицу координат:
Шаг 3: Точки пересечения с прямой
Решаем уравнение для нахождения точек пересечения с прямой :
Рассмотрим три возможных случая:
Если (то есть ):
Если (то есть ):
Если :
Таким образом, точки пересечения:
Ответ: ;
График функции:
График функции представляет собой линию с двумя точками излома в точках и , с двумя отрезками, которые соединяются в этих точках.
Итог:
- : не пересекает прямую .
- : пересекает прямую в точках и .
- : пересекает прямую в точках и .




Оставь свой отзыв 💬
Комментариев пока нет, будьте первым!