
Учебник «Алгебра» для 10-11 классов под авторством Алимова – это один из наиболее популярных и широко используемых учебных пособий для старшеклассников. Он заслужил признание как среди учителей, так и среди учеников благодаря своей структурированности, доступности изложения и качественной проработке материала.
ГДЗ по Алгебре 10-11 Класс Номер 1416 Алимов — Подробные Ответы
С помощью графика решить неравенство:
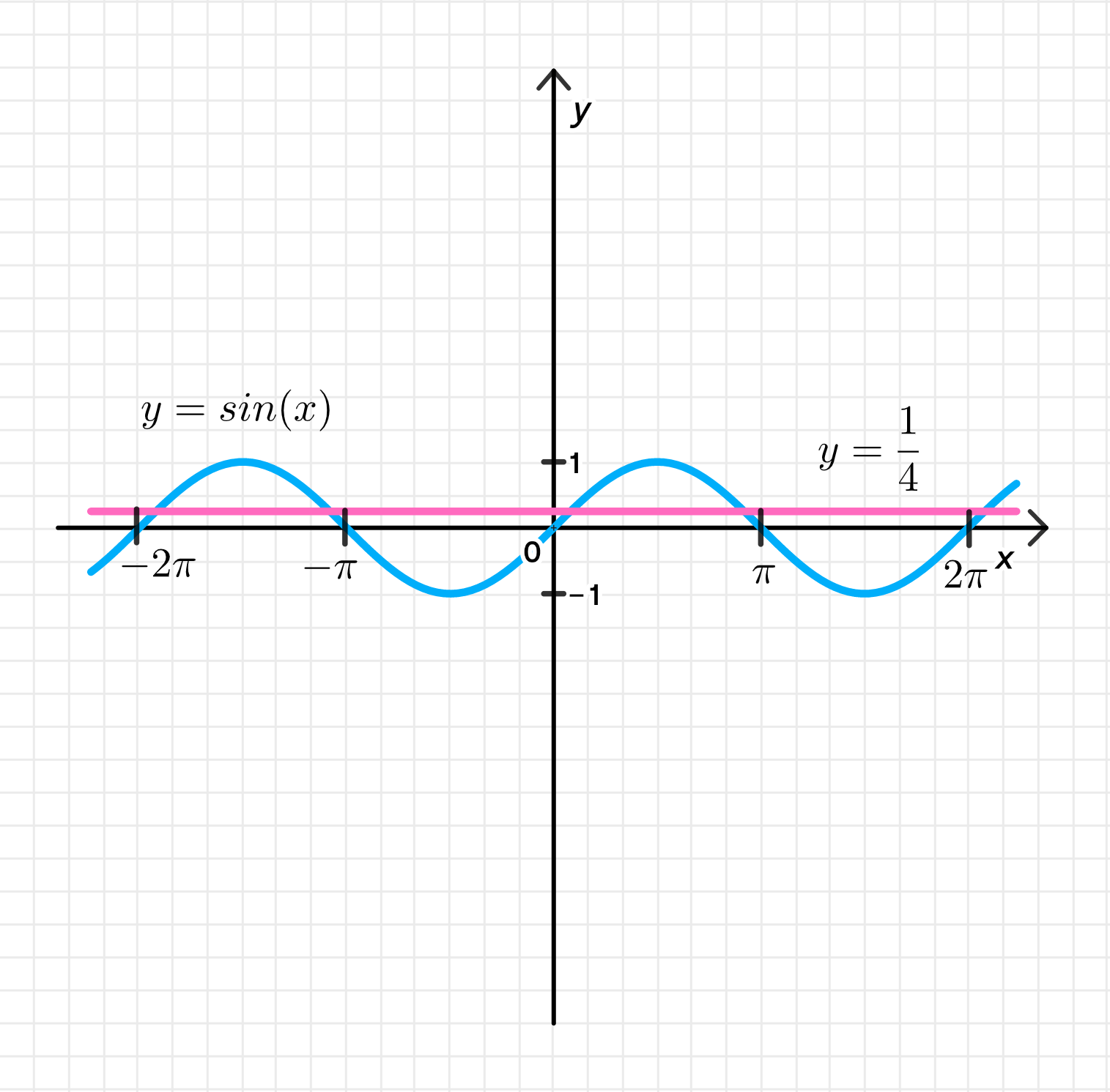
- sin х < 1/4;
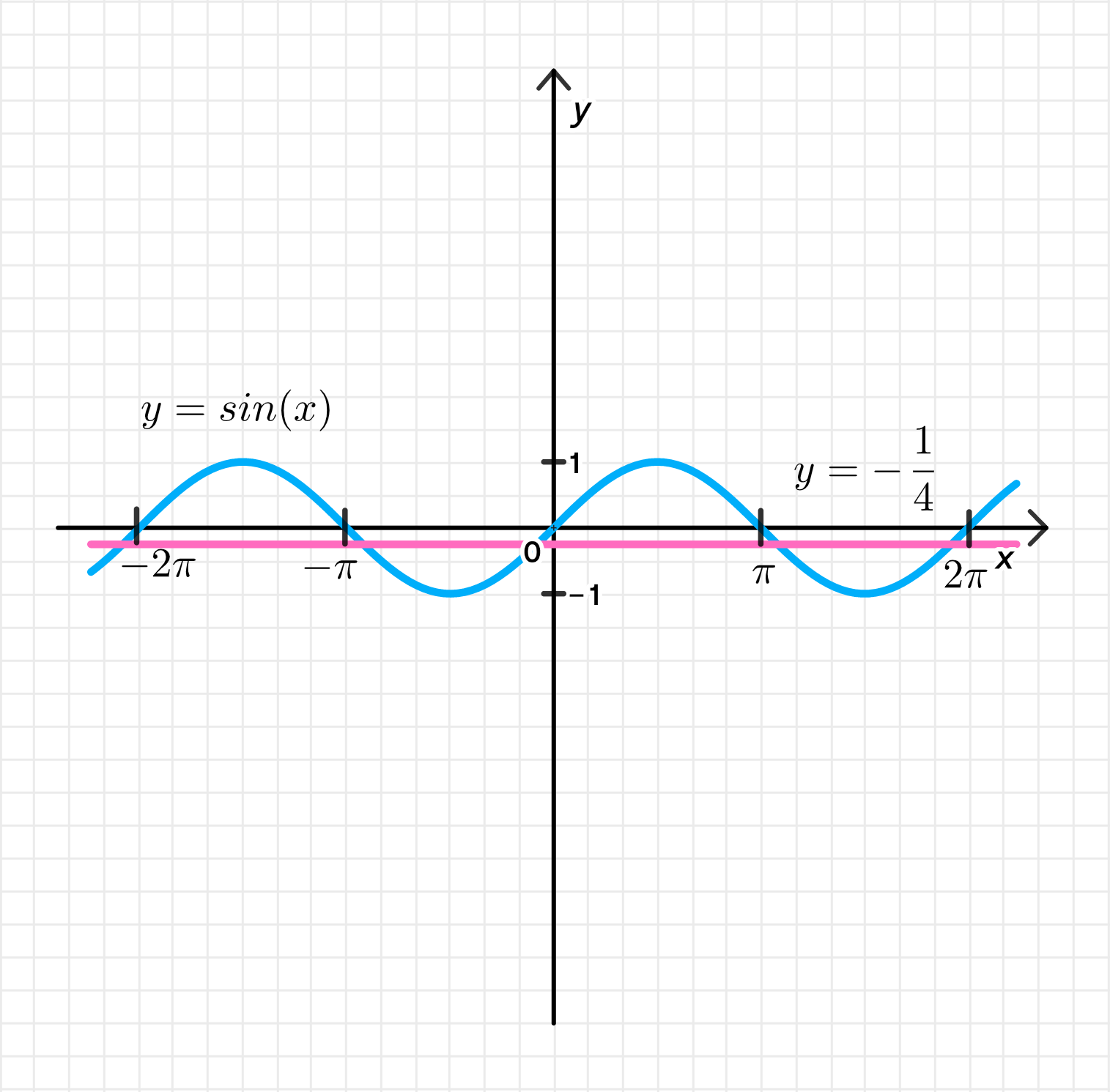
- sin х > -1/4
- tg х — 3 < =0;
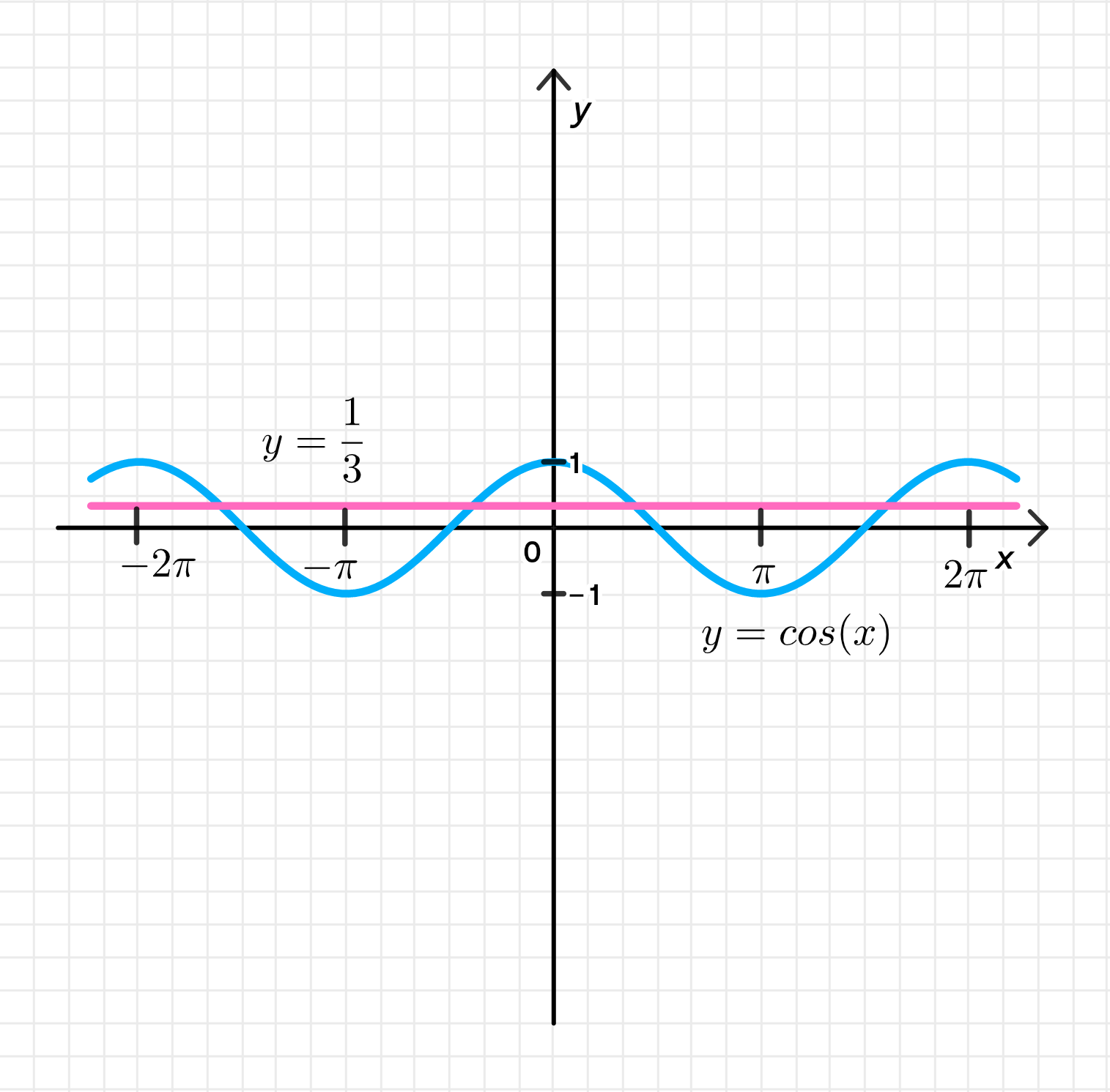
- cos х > 1/3.
;
;
Графики функций и :
Ответ: .
;
;
Графики функций и :
Ответ: .
;
;
;
Графики функций и :
Ответ: .
;
;
Графики функций и :
Ответ: .
Задача 1:
Шаг 1: Разбираем неравенство
Сначала обратим внимание на то, что — периодическая функция с периодом , а ее значения лежат в интервале .
Нам нужно найти , такие что:
Для этого нужно найти, где график функции ниже горизонтальной линии .
Шаг 2: Находим соответствующие углы
Для того чтобы решить это неравенство, нужно найти углы, для которых .
Эти углы можно найти с помощью арксинуса:
При этом функция принимает значение в двух местах на каждом интервале длиной : в первом и втором квадрантах.
Таким образом, неравенство выполняется между этими двумя углами.
Шаг 3: Применяем периодичность функции
Поскольку периодична с периодом , то решение будет иметь вид:
где .
Ответ:
Задача 2:
Шаг 1: Разбираем неравенство
Теперь рассматриваем неравенство . Суть задачи заключается в том, чтобы найти такие , для которых график функции выше горизонтальной линии .
Шаг 2: Находим соответствующие углы
Аналогично предыдущему шагу, для нахождения углов, где , применим арксинус:
Это значение угла также будет иметь два решения на интервале длиной , и неравенство будет выполняться между этими двумя углами.
Шаг 3: Применяем периодичность функции
Решение будет иметь вид:
где .
Ответ:
Задача 3:
Шаг 1: Преобразуем неравенство
Рассмотрим неравенство , которое можно переписать как:
Задача состоит в том, чтобы найти такие значения , для которых тангенс не превышает 3.
Шаг 2: Находим соответствующие углы
Для того чтобы найти, где , применим арктангенс:
Тангенс — периодическая функция с периодом , поэтому решение будет повторяться через .
Шаг 3: Применяем периодичность функции
Решение неравенства будет в интервале от до на каждом периоде . Поэтому решение будет:
где .
Ответ:
Задача 4:
Шаг 1: Разбираем неравенство
Неравенство означает, что нам нужно найти такие значения , для которых график функции выше или равен горизонтальной линии .
Шаг 2: Находим соответствующие углы
Для того чтобы найти, где , применим арккосинус:
Это решение дает два угла: один в первом квадранте и один во втором квадранте. Мы знаем, что — четная функция, и на каждом интервале длиной решение будет повторяться.
Шаг 3: Применяем периодичность функции
Решение будет таким:
где .
Ответ:


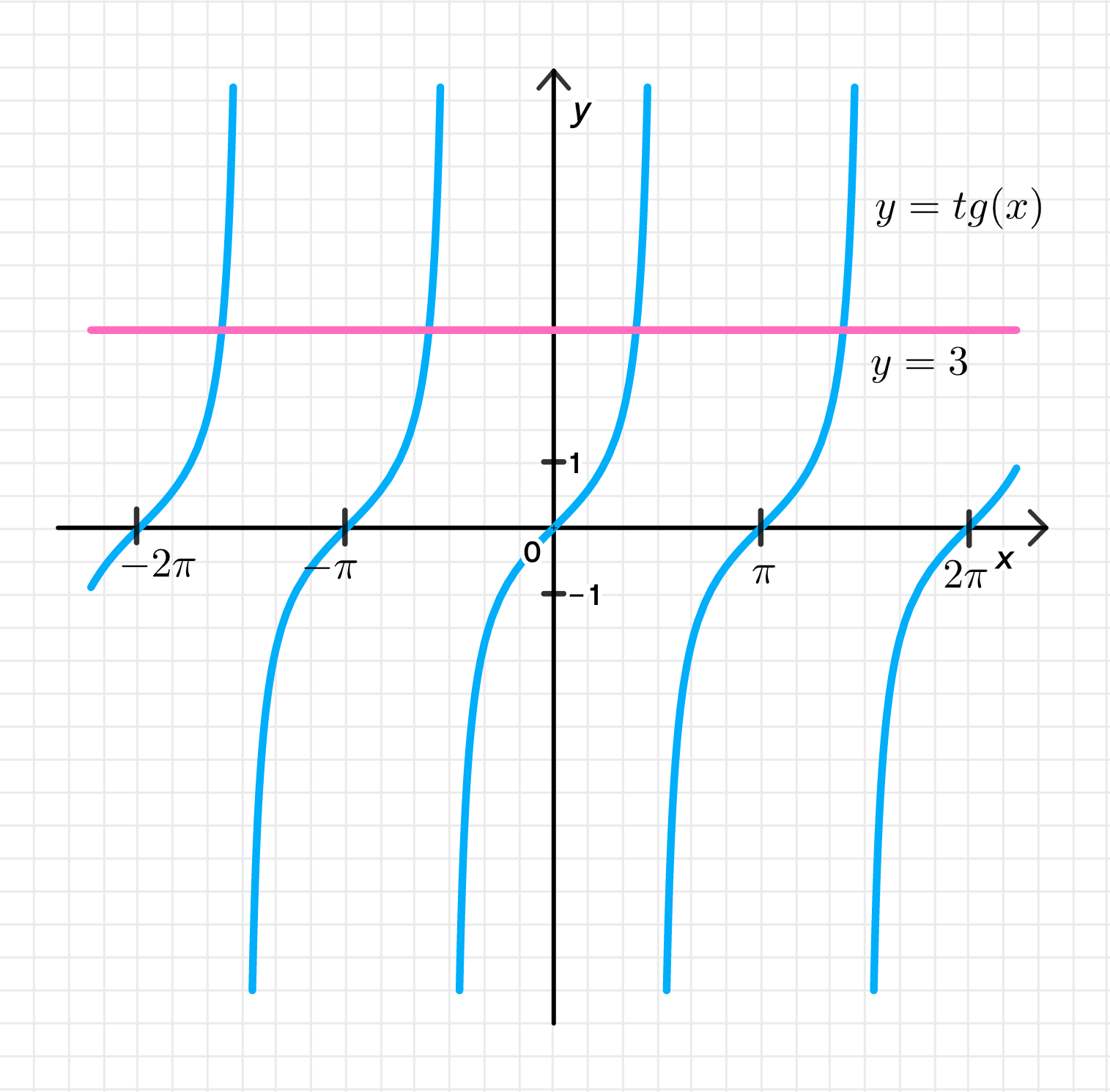

Оставь свой отзыв 💬
Комментариев пока нет, будьте первым!