ГДЗ по Алгебре 10-11 Класс Учебник 📕 Алимов — Все Части

Алгебра

10-11 класс учебник Алимов

10 класс

Тип

ГДЗ, Решебник.

Автор

Ш.А. Алимов, Ю.М. Колягин, М.В. Ткачева.

Год

2015-2024.

Издательство

Просвещение.

Описание

Учебник «Алгебра» для 10-11 классов под авторством Алимова – это один из наиболее популярных и широко используемых учебных пособий для старшеклассников. Он заслужил признание как среди учителей, так и среди учеников благодаря своей структурированности, доступности изложения и качественной проработке материала.

Учебник охватывает весь необходимый курс алгебры для 10-11 классов, включая такие сложные темы, как производные, интегралы, логарифмы и элементы математического анализа. Материал представлен последовательно и логично, что позволяет ученикам постепенно углубляться в изучение предмета. Пособие включает как теоретическую часть, так и большое количество практических заданий различного уровня сложности, что способствует закреплению знаний.

Одной из главных особенностей учебника является наличие задач повышенной сложности, которые стимулируют развитие логического мышления и навыков решения нестандартных задач. Кроме того, в книге представлены примеры из реальной жизни, что делает изучение алгебры более интересным и прикладным.

Преимущества учебника

Четкая структура материала
Учебник разделен на главы и параграфы с последовательным изложением тем. Это позволяет ученикам легко ориентироваться в содержании и возвращаться к ранее изученным темам для повторения.
Пошаговые объяснения
Каждая новая тема сопровождается подробными примерами с пошаговым решением. Это помогает ученикам лучше понять алгоритмы выполнения задач.
Разнообразие упражнений
В учебнике представлены задачи разного уровня сложности: от базовых до олимпиадных. Это делает пособие полезным как для обычных школьников, так и для тех, кто готовится к экзаменам или олимпиадам.
Практическая направленность
Включение задач из реальной жизни (например, расчет процентов или использование математических моделей) помогает ученикам видеть практическое применение алгебры.
Подготовка к ЕГЭ
Учебник содержит задания, аналогичные тем, которые встречаются на ЕГЭ, что делает его отличным инструментом для подготовки к экзаменам.

Учебник «Алгебра» Алимова для 10-11 классов – это надежный помощник в изучении математики. Он подходит как для базового освоения предмета, так и для углубленного изучения. Благодаря четкой структуре, разнообразию заданий и ориентации на экзамены, данный учебник является одним из лучших выборов для старшеклассников.

ГДЗ по Алгебре 10-11 Класс Номер 1386 Алимов — Подробные Ответы

Задача

Решить графически уравнение:

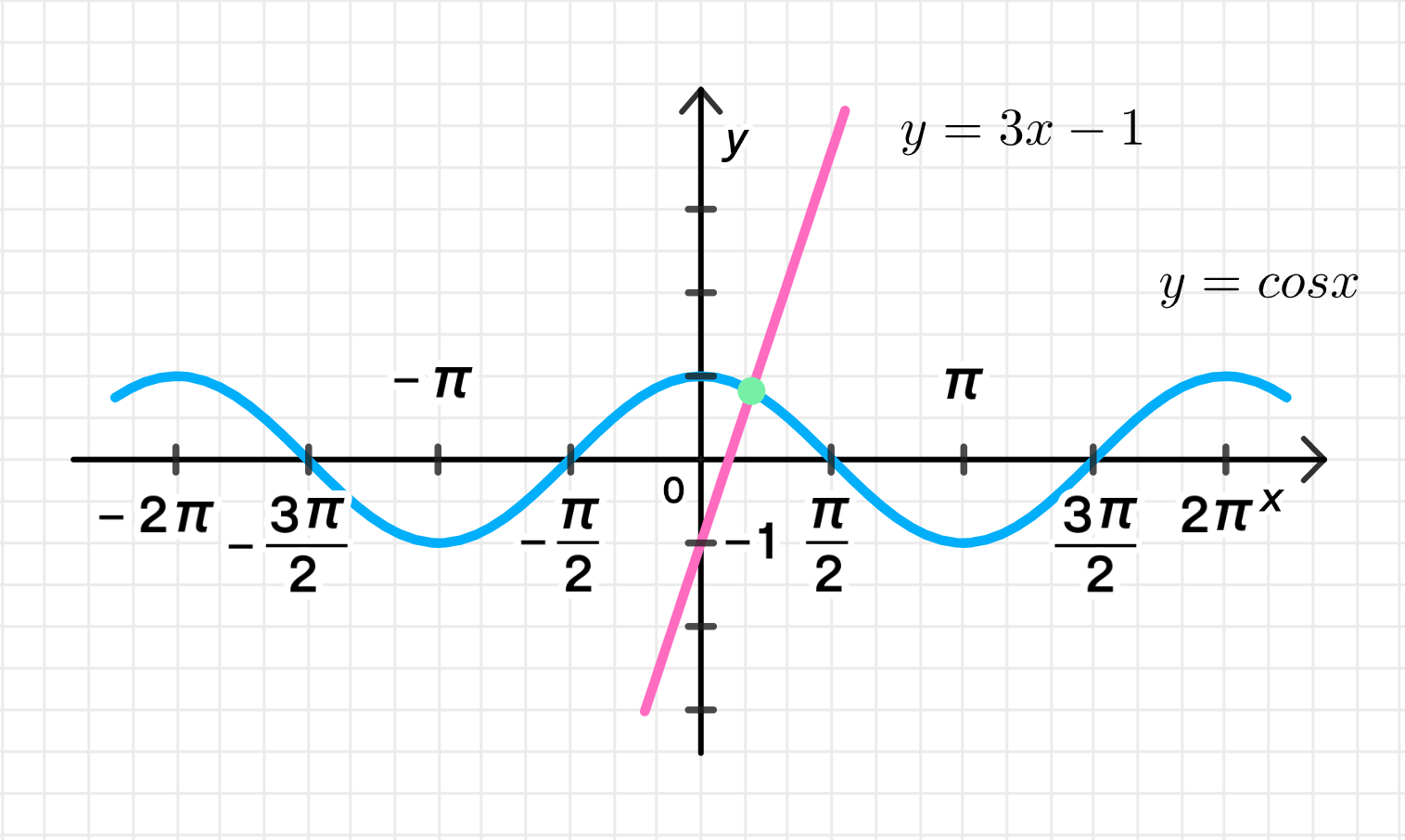
cos х = Зх — 1;
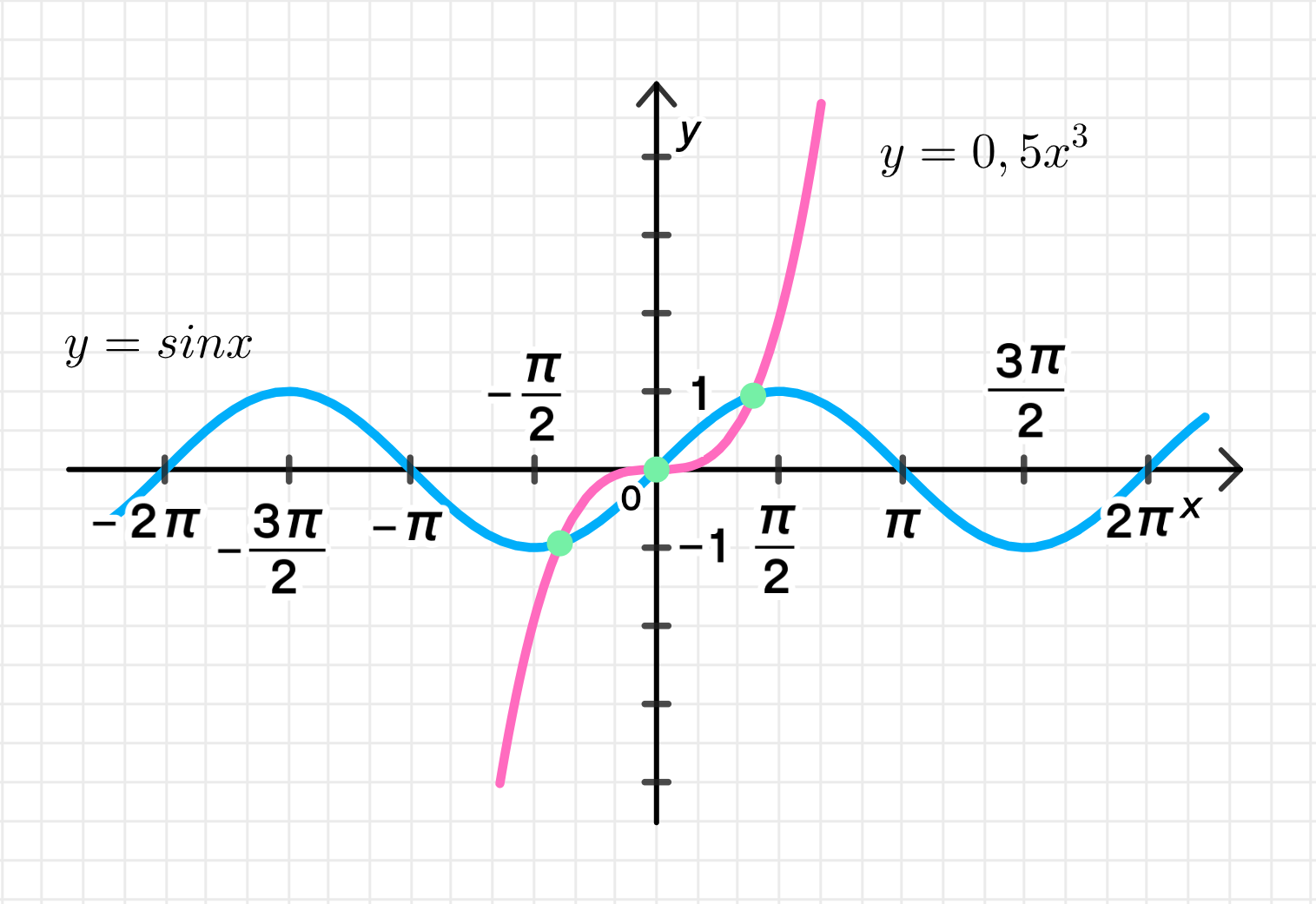
sin х = 0,5х3;
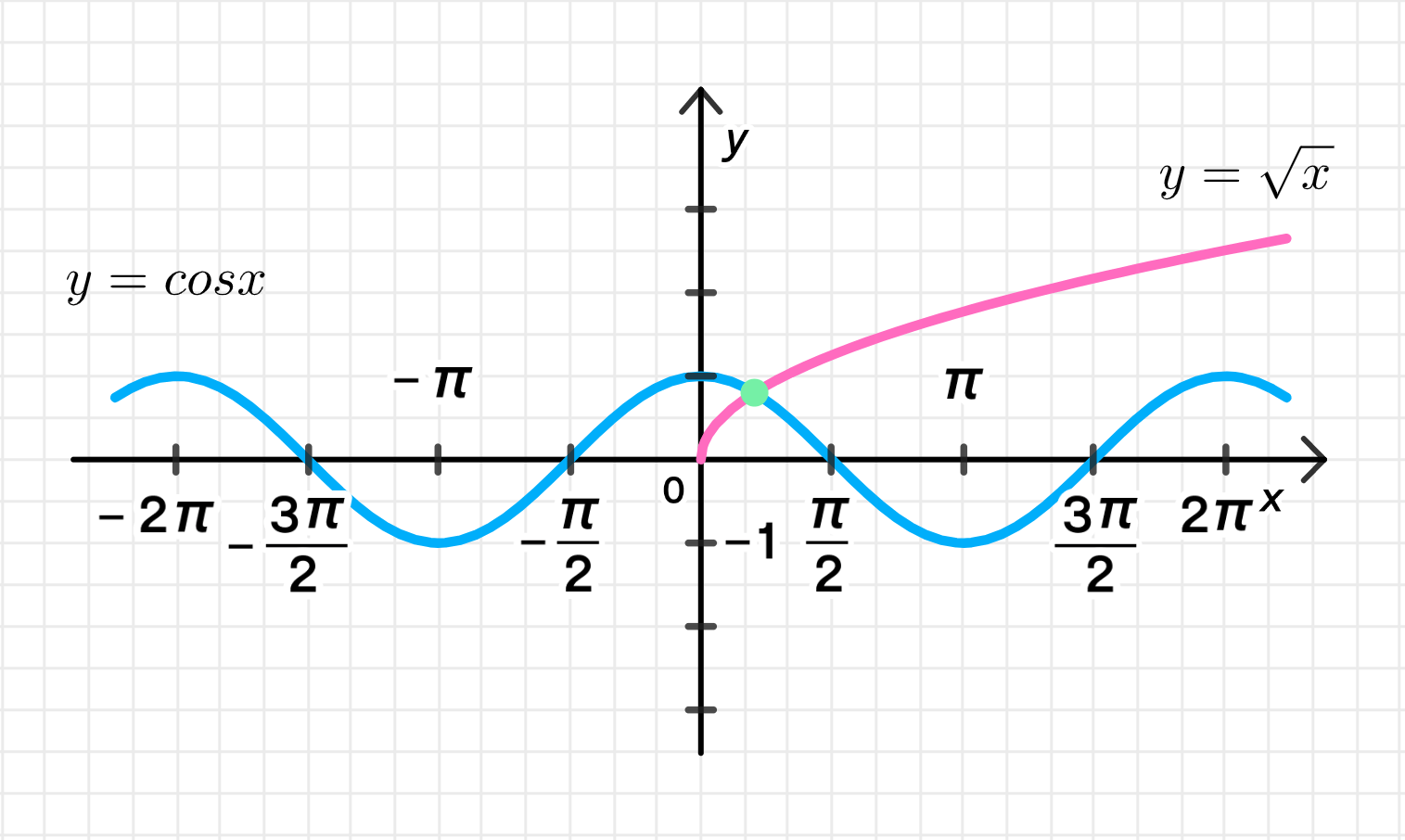
cos х = корень х;
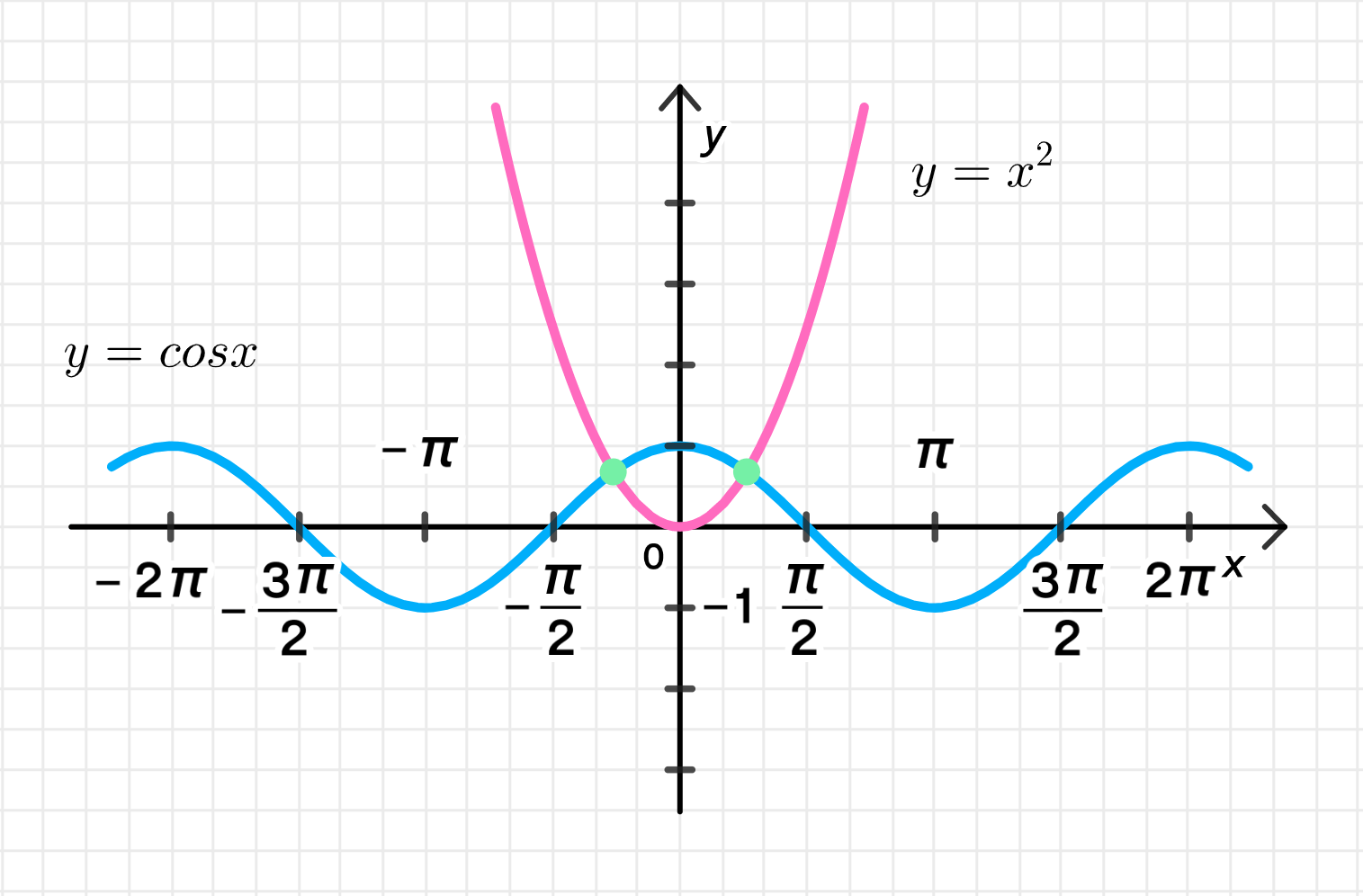
cos х = х2.

Краткий ответ:

$\cos x = 3x — 1;$

$y = \cos x$ — элементарная тригонометрическая функция;
$y = 3x — 1$ — уравнение прямой:

$x$	1	0	3
$y$	2	-1	8

Графики функций:

Ответ: $x \approx 0.6$ .

$\sin x = 0.5x^3;$

$y = \sin x$ — элементарная тригонометрическая функция;
$y = 0.5x^3$ — уравнение кубической параболы:

$x$	-3	-2	0	2	3
$y$	-4.5	-4	0	4	4.5

Графики функций:

Ответ: $x_1 = 0$ ; $x_2 \approx \pm 1.2$ .

$\cos x = \sqrt{x};$

$y = \cos x$ — элементарная тригонометрическая функция;
$y = \sqrt{x}$ — уравнение ветви параболы:

$x$	0	1	9
$y$	0	1	3

Графики функций:

Ответ: $x \approx 0.6$ .

$\cos x = x^2;$

$y = \cos x$ — элементарная тригонометрическая функция;
$y = x^2$ — уравнение параболы:

$x$	-3	-1	0	1	3
$y$	9	1	0	1	9

Графики функций:

Ответ: $x \approx \pm 0.8$ .

Подробный ответ:

Задача 1: $\cos x = 3x — 1$

Шаг 1: Формулировка уравнения и определение функций.

Уравнение имеет вид:

$\cos x = 3x — 1.$

$y = \cos x$ — это элементарная тригонометрическая функция (косинус), которая имеет период $2\pi$ , а также принимает значения от $-1$ до $1$ .
$y = 3x — 1$ — это уравнение прямой, которая имеет угловой коэффициент 3 и пересекает ось $y$ в точке $-1$ .

Шаг 2: Исследование графиков функций.

Для того чтобы найти решение уравнения, нужно определить, где графики этих двух функций пересекаются.

$x$	1	0	3
$y$	2	-1	8

Для $x = 1$ , $\cos 1 \approx 0.5403$ и $3(1) — 1 = 2$ .
Для $x = 0$ , $\cos 0 = 1$ и $3(0) — 1 = -1$ .
Для $x = 3$ , $\cos 3 \approx -0.98999$ и $3(3) — 1 = 8$ .

Шаг 3: Нахождение решения.

Графики функций пересекаются где-то между $x = 0$ и $x = 1$ , так как значение функции косинуса на интервале $[0,1]$ меняется от 1 до 0, а прямая $3x — 1$ на том же интервале от $-1$ до 2. Ожидаем, что решение будет примерно в точке, где графики этих функций пересекаются.

Шаг 4: Приближенное решение.

Используя численные методы или графический калькулятор, можно найти, что решение уравнения:

$x \approx 0.6.$

Ответ: $x \approx 0.6$ .

Задача 2: $\sin x = 0.5x^3$

Шаг 1: Формулировка уравнения и определение функций.

Уравнение:

$\sin x = 0.5x^3.$

$y = \sin x$ — это элементарная тригонометрическая функция, которая колеблется между $-1$ и $1$ с периодом $2\pi$ .
$y = 0.5x^3$ — это кубическая парабола, которая при $x = 0$ равна 0 и растет при $x > 0$ , а для $x < 0$ стремится к минус бесконечности.

Шаг 2: Исследование графиков функций.

Для того чтобы найти решение уравнения, нужно определить, где графики этих двух функций пересекаются.

$x$	-3	-2	0	2	3
$y$	-4.5	-4	0	4	4.5

Для $x = -3$ , $\sin(-3) \approx -0.1411$ и $0.5(-3)^3 = -13.5$ .
Для $x = -2$ , $\sin(-2) \approx -0.9093$ и $0.5(-2)^3 = -4$ .
Для $x = 0$ , $\sin(0) = 0$ и $0.5(0)^3 = 0$ .
Для $x = 2$ , $\sin(2) \approx 0.9093$ и $0.5(2)^3 = 4$ .
Для $x = 3$ , $\sin(3) \approx 0.1411$ и $0.5(3)^3 = 13.5$ .

Шаг 3: Нахождение решения.

Графики функций пересекаются при $x = 0$ и еще приблизительно при $x \approx \pm 1.2$ .

Шаг 4: Приближенное решение.

Используя численные методы (например, метод Ньютона или графический калькулятор), можно найти, что $x \approx \pm 1.2$ .

Ответ: $x_1 = 0$ ; $x_2 \approx \pm 1.2$ .

Задача 3: $\cos x = \sqrt{x}$

Шаг 1: Формулировка уравнения и определение функций.

Уравнение:

$\cos x = \sqrt{x}.$

$y = \cos x$ — это элементарная тригонометрическая функция, которая колеблется между $-1$ и $1$ с периодом $2\pi$ .
$y = \sqrt{x}$ — это функция, определенная только для $x \geq 0$ , и она монотонно возрастает.

Шаг 2: Исследование графиков функций.

Для того чтобы найти решение уравнения, нужно определить, где графики этих двух функций пересекаются.

$x$	0	1	9
$y$	0	1	3

Для $x = 0$ , $\cos(0) = 1$ и $\sqrt{0} = 0$ .
Для $x = 1$ , $\cos(1) \approx 0.5403$ и $\sqrt{1} = 1$ .
Для $x = 9$ , $\cos(9) \approx -0.9117$ и $\sqrt{9} = 3$ .

Шаг 3: Нахождение решения.

Графики функций пересекаются примерно при $x \approx 0.6$ , так как значения функции косинуса и функции корня близки на этом интервале.

Шаг 4: Приближенное решение.

Используя численные методы, можно найти, что решение уравнения:

$x \approx 0.6.$

Ответ: $x \approx 0.6$ .

Задача 4: $\cos x = x^2$

Шаг 1: Формулировка уравнения и определение функций.

Уравнение:

$\cos x = x^2.$

$y = \cos x$ — это элементарная тригонометрическая функция, которая колеблется между $-1$ и $1$ с периодом $2\pi$ .
$y = x^2$ — это парабола, которая возрастает на обеих сторонах от $x = 0$ .

Шаг 2: Исследование графиков функций.

Для того чтобы найти решение уравнения, нужно определить, где графики этих двух функций пересекаются.

$x$	-3	-1	0	1	3
$y$	9	1	0	1	9

Для $x = -3$ , $\cos(-3) \approx -0.98999$ и $(-3)^2 = 9$ .
Для $x = -1$ , $\cos(-1) \approx 0.5403$ и $(-1)^2 = 1$ .
Для $x = 0$ , $\cos(0) = 1$ и $0^2 = 0$ .
Для $x = 1$ , $\cos(1) \approx 0.5403$ и $1^2 = 1$ .
Для $x = 3$ , $\cos(3) \approx -0.98999$ и $3^2 = 9$ .

Шаг 3: Нахождение решения.

Графики функций пересекаются примерно при $x \approx \pm 0.8$ .

Шаг 4: Приближенное решение.

Используя численные методы, можно найти, что решение уравнения:

$x \approx \pm 0.8.$

Ответ: $x \approx \pm 0.8$ .

Оцени решение

← Предыдущий Следующий →

Сообщить об ошибке

Задачи для внеклассной работы