Краткий ответ:
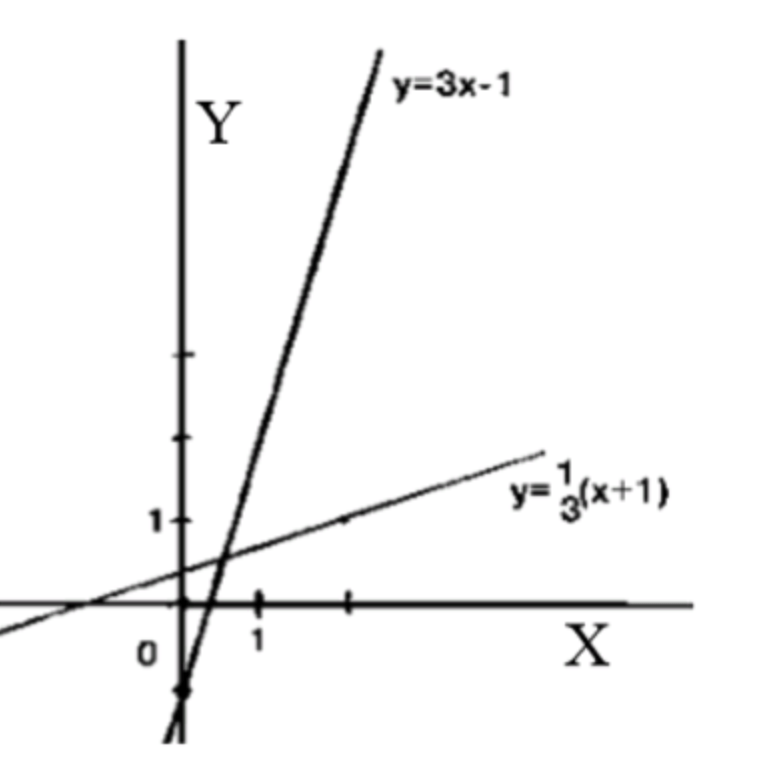
1) y = 3 x − 1 y = 3x — 1
Основная функция:
Область определения: x ∈ R x \in \mathbb{R} Множество значений: y ∈ R y \in \mathbb{R} x 0 1 y − 1 2 \begin{array}{|c|c|c|} \hline x & 0 & 1 \\ \hline y & -1 & 2 \\ \hline \end{array}
Обратная функция:
x = 3 y − 1 3 y = x + 1 y = x + 1 3 x = 3y — 1 \\ 3y = x + 1 \\ y = \frac{x + 1}{3}
Область определения: x ∈ R x \in \mathbb{R} Множество значений: y ∈ R y \in \mathbb{R} x 2 0 y 1 1 3
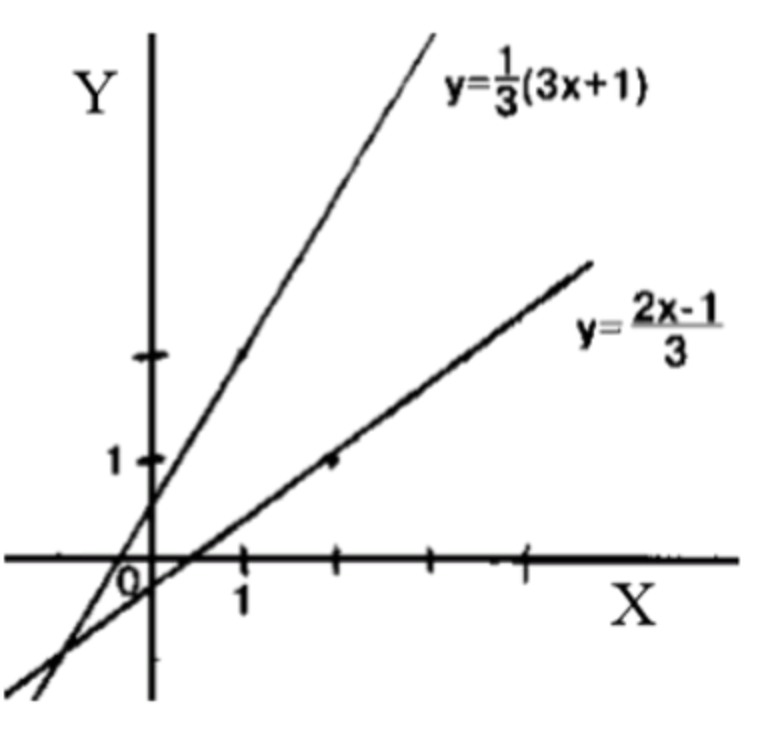
\begin{array}{|c|c|c|} \hline x & 2 & 0 \\ \hline y & 1 & \frac{1}{3} \\ \hline \end{array} y = 2 x − 1 3 y = \frac{2x — 1}{3}
Основная функция:
Область определения: x ∈ R x \in \mathbb{R} Множество значений: y ∈ R y \in \mathbb{R} x − 1 2 y − 1 1 \begin{array}{|c|c|c|} \hline x & -1 & 2 \\ \hline y & -1 & 1 \\ \hline \end{array}
Обратная функция:
x = 2 y − 1 3 3 x = 2 y − 1 2 y = 3 x + 1 y = 3 x + 1 2 x = \frac{2y — 1}{3} \\ 3x = 2y — 1 \\ 2y = 3x + 1 \\ y = \frac{3x + 1}{2}
Область определения: x ∈ R x \in \mathbb{R} Множество значений: y ∈ R y \in \mathbb{R} x − 1 1 y − 1 2
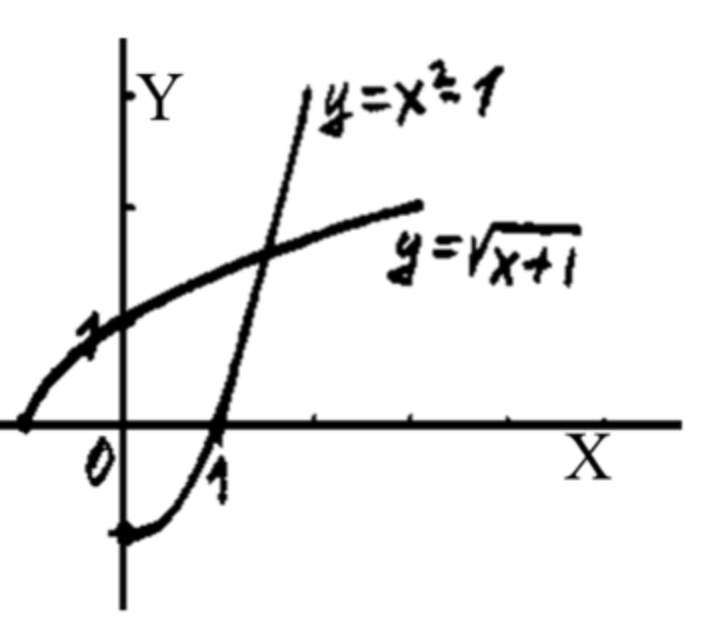
\begin{array}{|c|c|c|} \hline x & -1 & 1 \\ \hline y & -1 & 2 \\ \hline \end{array} y = x 2 − 1 y = x^2 — 1 x ≥ 0 x \geq 0
Основная функция:
Область определения: x ≥ 0 x \geq 0 Множество значений: y ≥ − 1 y \geq -1 x − 1 1 2 3 y − 1 0 3 8 \begin{array}{|c|c|c|c|c|} \hline x & -1 & 1 & 2 & 3 \\ \hline y & -1 & 0 & 3 & 8 \\ \hline \end{array}
Обратная функция:
x = y 2 − 1 y 2 = x + 1 y = x + 1 x = y^2 — 1 \\ y^2 = x + 1 \\ y = \sqrt{x + 1}
Область определения: x ≥ − 1 x \geq -1 Множество значений: y ≥ 0 y \geq 0 x − 1 0 3 8 y 0 1 2 3
\begin{array}{|c|c|c|c|c|} \hline x & -1 & 0 & 3 & 8 \\ \hline y & 0 & 1 & 2 & 3 \\ \hline \end{array}
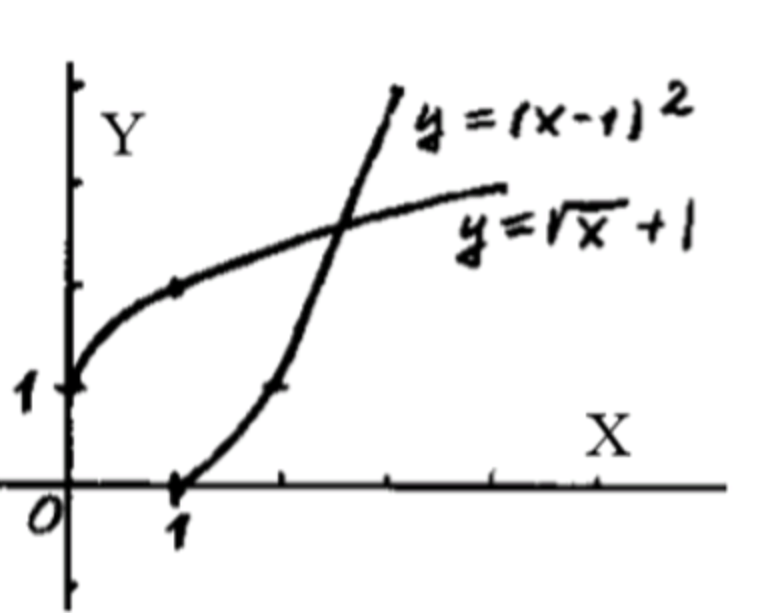
4) y = ( x − 1 ) 2 y = (x — 1)^2 x ≥ 1 x \geq 1
Основная функция:
Область определения: x ≥ 1 x \geq 1 Множество значений: y ≥ 0 y \geq 0 x 1 2 3 4 y 0 1 4 9 \begin{array}{|c|c|c|c|c|} \hline x & 1 & 2 & 3 & 4 \\ \hline y & 0 & 1 & 4 & 9 \\ \hline \end{array}
Обратная функция:
x = ( y − 1 ) 2 x = y − 1 y = x + 1 x = (y — 1)^2 \\ \sqrt{x} = y — 1 \\ y = \sqrt{x} + 1
Область определения: x ≥ 0 x \geq 0 Множество значений: y ≥ 1 y \geq 1 x 0 1 4 9 y 1 2 3 4 \begin{array}{|c|c|c|c|c|} \hline x & 0 & 1 & 4 & 9 \\ \hline y & 1 & 2 & 3 & 4 \\ \hline \end{array}
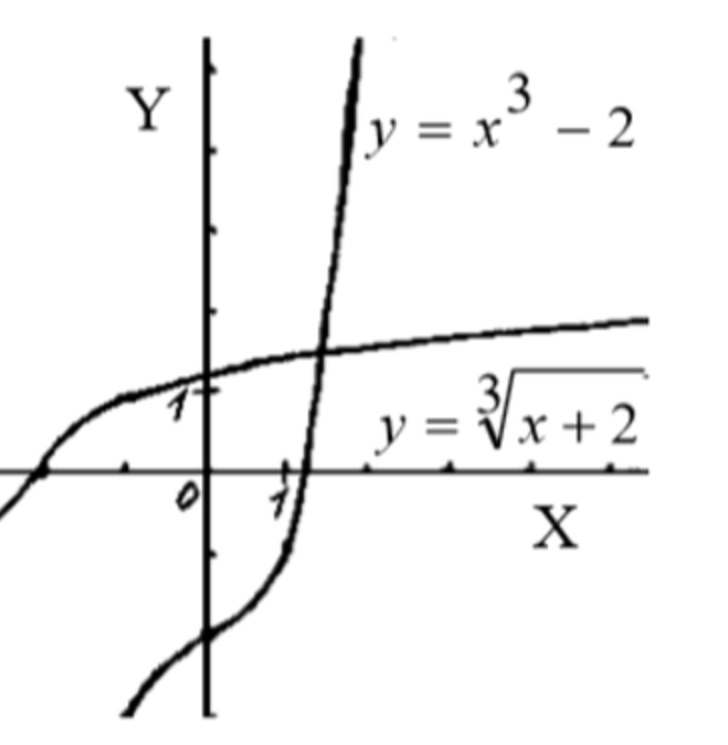
5) y = x 3 − 2 y = x^3 — 2
Основная функция:
Область определения: x ∈ R x \in \mathbb{R} Множество значений: y ∈ R y \in \mathbb{R} x − 2 − 1 0 1 2 y − 10 − 3 − 2 − 1 6 \begin{array}{|c|c|c|c|c|} \hline x & -2 & -1 & 0 & 1 & 2 \\ \hline y & -10 & -3 & -2 & -1 & 6 \\ \hline \end{array}
Обратная функция:
x = y 3 − 2 y 3 = x + 2 y = x + 2 3 x = y^3 — 2 \\ y^3 = x + 2 \\ y = \sqrt[3]{x + 2}
Область определения: x ∈ R x \in \mathbb{R} Множество значений: y ∈ R y \in \mathbb{R} x − 10 − 3 − 2 − 1 6 y − 1 0 1 2 8 3 = 2 \begin{array}{|c|c|c|c|c|} \hline x & -10 & -3 & -2 & -1 & 6 \\ \hline y & -1 & 0 & 1 & 2 & \sqrt[3]{8} = 2 \\ \hline \end{array}
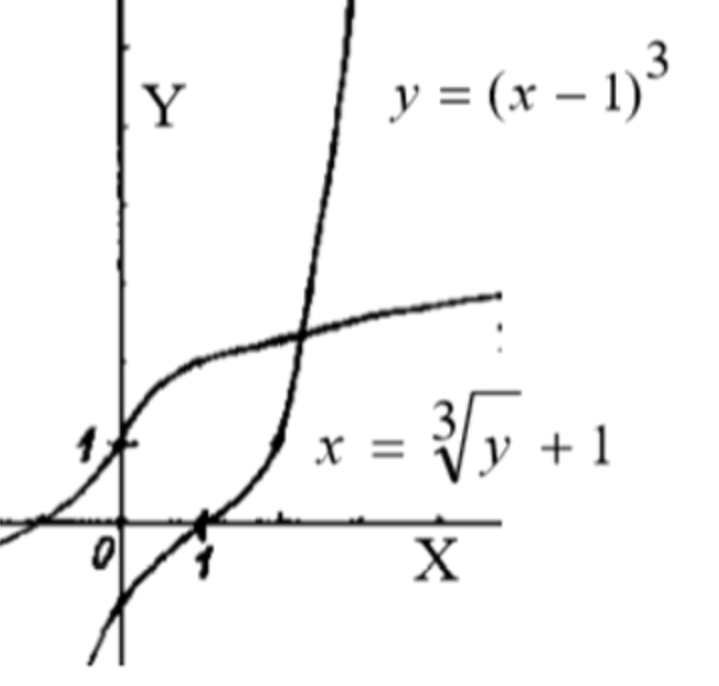
6) y = ( x − 1 ) 3 y = (x — 1)^3
Основная функция:
Область определения: x ∈ R x \in \mathbb{R} Множество значений: y ∈ R y \in \mathbb{R} x − 1 0 1 2 3 y − 8 − 1 0 1 8 \begin{array}{|c|c|c|c|c|c|} \hline x & -1 & 0 & 1 & 2 & 3 \\ \hline y & -8 & -1 & 0 & 1 & 8 \\ \hline \end{array}
Обратная функция:
x = ( y − 1 ) 3 x 3 = y − 1 y = x 3 + 1 x = (y — 1)^3 \\ \sqrt[3]{x} = y — 1 \\ y = \sqrt[3]{x} + 1
Область определения: x ∈ R x \in \mathbb{R} Множество значений: y ∈ R y \in \mathbb{R} x − 8 − 1 0 1 8 y 0 1 2 3 \begin{array}{|c|c|c|c|c|} \hline x & -8 & -1 & 0 & 1 & 8 \\ \hline y & 0 & 1 & 2 & 3 & \\ \hline \end{array}
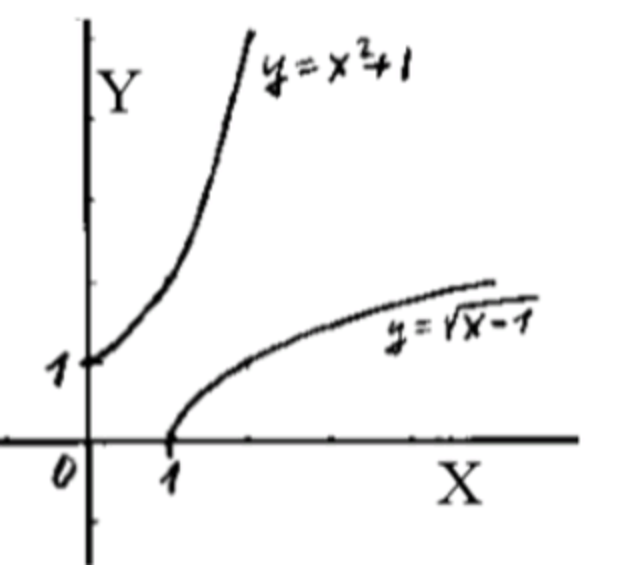
7) y = x − 1 y = \sqrt{x — 1}
Основная функция:
Область определения: x ≥ 1 x \geq 1 Множество значений: y ≥ 0 y \geq 0 x 1 5 10 y 0 2 3 \begin{array}{|c|c|c|} \hline x & 1 & 5 & 10 \\ \hline y & 0 & 2 & 3 \\ \hline \end{array}
Обратная функция:
x = y − 1 x 2 = y − 1 y = x 2 + 1 x = \sqrt{y — 1} \\ x^2 = y — 1 \\ y = x^2 + 1
Область определения: x ≥ 0 x \geq 0 Множество значений: y ≥ 1 y \geq 1 x 0 2 3 y 1 5 10 \begin{array}{|c|c|c|} \hline x & 0 & 2 & 3 \\ \hline y & 1 & 5 & 10 \\ \hline \end{array}
8) y = x + 1 y = \sqrt{x} + 1
Основная функция:
Область определения: x ≥ 0 x \geq 0 Множество значений: y ≥ 1 y \geq 1 x 0 4 9 y 1 3 4 \begin{array}{|c|c|c|} \hline x & 0 & 4 & 9 \\ \hline y & 1 & 3 & 4 \\ \hline \end{array}
Обратная функция:
x = y + 1 y = x − 1 y = ( x − 1 ) 2 x = \sqrt{y} + 1 \\ \sqrt{y} = x — 1 \\ y = (x — 1)^2
Область определения: x ≥ 1 x \geq 1 Множество значений: y ≥ 0 y \geq 0 x 1 3 4 y 0 4 9
\begin{array}{|c|c|c|c|} \hline x & 1 & 3 & 4 \\ \hline y & 0 & 4 & 9 \\ \hline \end{array}
Подробный ответ:
1) y = 3 x − 1 y = 3x — 1
Тип:
Линейная функция: коэффициент наклона k = 3 k = 3
Алгебраическое обращение:
y = 3 x − 1 ⇒ x = y + 1 3 ⇒ y − 1 = x + 1 3 y = 3x — 1 \Rightarrow x = \frac{y + 1}{3} \Rightarrow y^{-1} = \frac{x + 1}{3}
Взаимная проверка:
Подставим в оригинал:
y ( x + 1 3 ) = 3 ⋅ x + 1 3 − 1 = x + 1 − 1 = x y\left(\frac{x + 1}{3}\right) = 3 \cdot \frac{x + 1}{3} — 1 = x + 1 — 1 = x
Область и значения:
Оригинал: x ∈ R , y ∈ R x \in \mathbb{R},\ y \in \mathbb{R} Обратная: x ∈ R , y ∈ R x \in \mathbb{R},\ y \in \mathbb{R} Монотонность:
Обе функции строго возрастает, т.к. производные положительны.
2) y = 2 x − 1 3 y = \frac{2x — 1}{3}
Тип:
Линейная, наклон k = 2 3 k = \frac{2}{3}
Алгебраическое обращение:
y = 2 x − 1 3 ⇒ 3 y = 2 x − 1 ⇒ x = 3 y + 1 2 y = \frac{2x — 1}{3} \Rightarrow 3y = 2x — 1 \Rightarrow x = \frac{3y + 1}{2}
Проверка:
y ( 3 x + 1 2 ) = 2 ⋅ ( 3 x + 1 2 ) − 1 3 = 3 x + 1 − 1 3 = x y\left(\frac{3x + 1}{2}\right) = \frac{2 \cdot \left(\frac{3x + 1}{2}\right) — 1}{3} = \frac{3x + 1 — 1}{3} = x
Область и значения:
Нет ограничений: R → R \mathbb{R} \to \mathbb{R}
Монотонность:
Обе функции строго возрастает.
3) y = x 2 − 1 y = x^2 — 1 x ≥ 0 x \geq 0
Тип:
Частичная парабола. Ограничено снизу: y ≥ − 1 y \geq -1
Обратная:
y = x 2 − 1 ⇒ x = y + 1 y = x^2 — 1 \Rightarrow x = \sqrt{y + 1}
Проверка:
y ( x + 1 ) = ( x + 1 ) 2 − 1 = x + 1 − 1 = x y(\sqrt{x + 1}) = (\sqrt{x + 1})^2 — 1 = x + 1 — 1 = x
Области:
Оригинал: x ≥ 0 , y ≥ − 1 x \geq 0,\ y \geq -1 Обратная: x ≥ − 1 , y ≥ 0 x \geq -1,\ y \geq 0 Монотонность:
Оригинал: возрастает на [ 0 , ∞ ) [0, \infty) Обратная: тоже возрастает
4) y = ( x − 1 ) 2 y = (x — 1)^2 x ≥ 1 x \geq 1
Тип:
Смещение параболы вправо на 1.
Обратная:
y = ( x − 1 ) 2 ⇒ x = y + 1 y = (x — 1)^2 \Rightarrow x = \sqrt{y} + 1
Проверка:
y ( x + 1 ) = ( x ) 2 = x y(\sqrt{x} + 1) = (\sqrt{x})^2 = x
Области:
Оригинал: x ≥ 1 , y ≥ 0 x \geq 1,\ y \geq 0 Обратная: x ≥ 0 , y ≥ 1 x \geq 0,\ y \geq 1
5) y = x 3 − 2 y = x^3 — 2
Тип:
Кубическая функция (нечётная), определена на всей R \mathbb{R}
Обратная:
y = x 3 − 2 ⇒ x = y + 2 3 y = x^3 — 2 \Rightarrow x = \sqrt[3]{y + 2}
Проверка:
y ( x + 2 3 ) = ( x + 2 3 ) 3 − 2 = x + 2 − 2 = x y(\sqrt[3]{x + 2}) = (\sqrt[3]{x + 2})^3 — 2 = x + 2 — 2 = x
Области:
Оригинал и обратная: R → R \mathbb{R} \to \mathbb{R} Монотонность:
Строго возрастает на всей области
6) y = ( x − 1 ) 3 y = (x — 1)^3
Тип:
Кубическая функция, сдвинута вправо на 1.
Обратная:
y = ( x − 1 ) 3 ⇒ x = y 3 + 1 y = (x — 1)^3 \Rightarrow x = \sqrt[3]{y} + 1
Проверка:
y ( x 3 + 1 ) = ( x 3 ) 3 = x y(\sqrt[3]{x} + 1) = (\sqrt[3]{x})^3 = x
Области:
Нет ограничений, вся R \mathbb{R}
Монотонность:
Обратимая без ограничений — функция строго возрастает
7) y = x − 1 y = \sqrt{x — 1}
Тип:
Корневая функция, определена при x ≥ 1 x \geq 1
Обратная:
x = y − 1 ⇒ y = x 2 + 1 x = \sqrt{y — 1} \Rightarrow y = x^2 + 1
Проверка:
y ( x − 1 ) = ( x − 1 ) 2 + 1 = x y(\sqrt{x — 1}) = (\sqrt{x — 1})^2 + 1 = x
Области:
Оригинал: x ≥ 1 , y ≥ 0 x \geq 1,\ y \geq 0 Обратная: x ≥ 0 , y ≥ 1 x \geq 0,\ y \geq 1 Монотонность:
Обе функции возрастают
8) y = x + 1 y = \sqrt{x} + 1
Тип:
Корневая функция, вертикальный сдвиг на 1 вверх
Обратная:
x = y + 1 ⇒ y = x − 1 ⇒ y = ( x − 1 ) 2 x = \sqrt{y} + 1 \Rightarrow \sqrt{y} = x — 1 \Rightarrow y = (x — 1)^2
Проверка:
y ( x + 1 ) = ( x ) 2 = x y(\sqrt{x} + 1) = (\sqrt{x})^2 = x
Области:
Оригинал: x ≥ 0 , y ≥ 1 x \geq 0,\ y \geq 1 Обратная: x ≥ 1 , y ≥ 0 x \geq 1,\ y \geq 0 Монотонность:
Обе функции возрастают на своих ОДЗ
Итог
№ Тип функции Ограничение Обратимая? Монотонность Область и значения 1 Линейная Нет Да Возрастает R → R \mathbb{R} \to \mathbb{R}
2 Линейная Нет Да Возрастает R → R \mathbb{R} \to \mathbb{R}
3 Квадрат x ≥ 0 x \geq 0
Да Возрастает [ 0 , ∞ ) → [ − 1 , ∞ ) [0, \infty) \to [-1, \infty)
4 Квадрат x ≥ 1 x \geq 1
Да Возрастает [ 1 , ∞ ) → [ 0 , ∞ ) [1, \infty) \to [0, \infty)
5 Куб Нет Да Возрастает R → R \mathbb{R} \to \mathbb{R}
6 Куб Нет Да Возрастает R → R \mathbb{R} \to \mathbb{R}
7 Корень x ≥ 1 x \geq 1
Да Возрастает [ 1 , ∞ ) → [ 0 , ∞ ) [1, \infty) \to [0, \infty)
8 Корень x ≥ 0 x \geq 0
Да Возрастает [ 0 , ∞ ) → [ 1 , ∞ ) [0, \infty) \to [1, \infty)



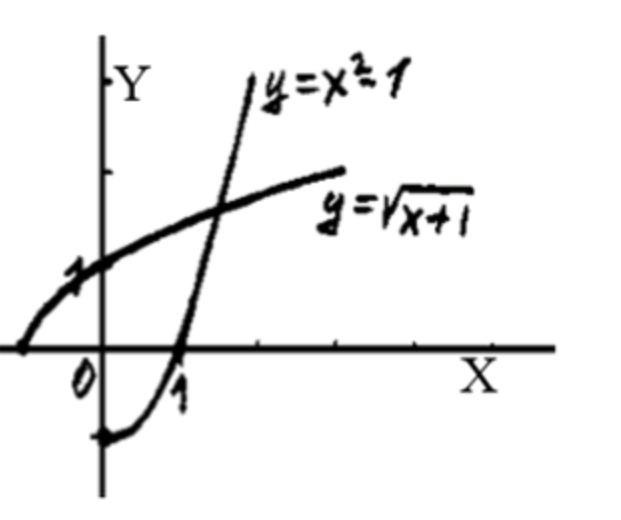

Оставь свой отзыв 💬
Комментариев пока нет, будьте первым!