
Учебник «Алгебра» для 10-11 классов под авторством Алимова – это один из наиболее популярных и широко используемых учебных пособий для старшеклассников. Он заслужил признание как среди учителей, так и среди учеников благодаря своей структурированности, доступности изложения и качественной проработке материала.
ГДЗ по Алгебре 10-11 Класс Номер 1361 Алимов — Подробные Ответы
Решить графически уравнение:
- 0,5х = 2х + 1;
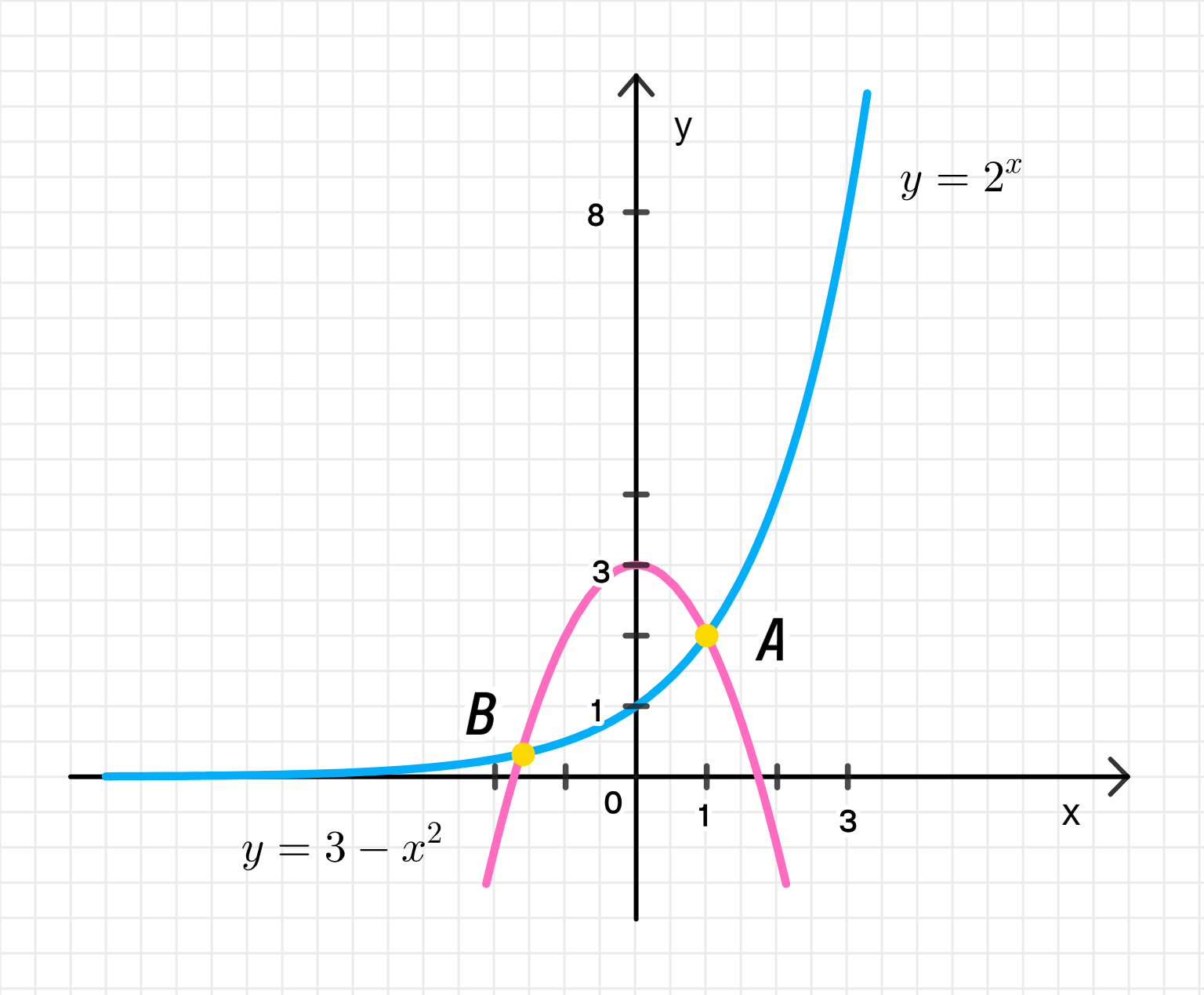
- 2х = 3 — х2;
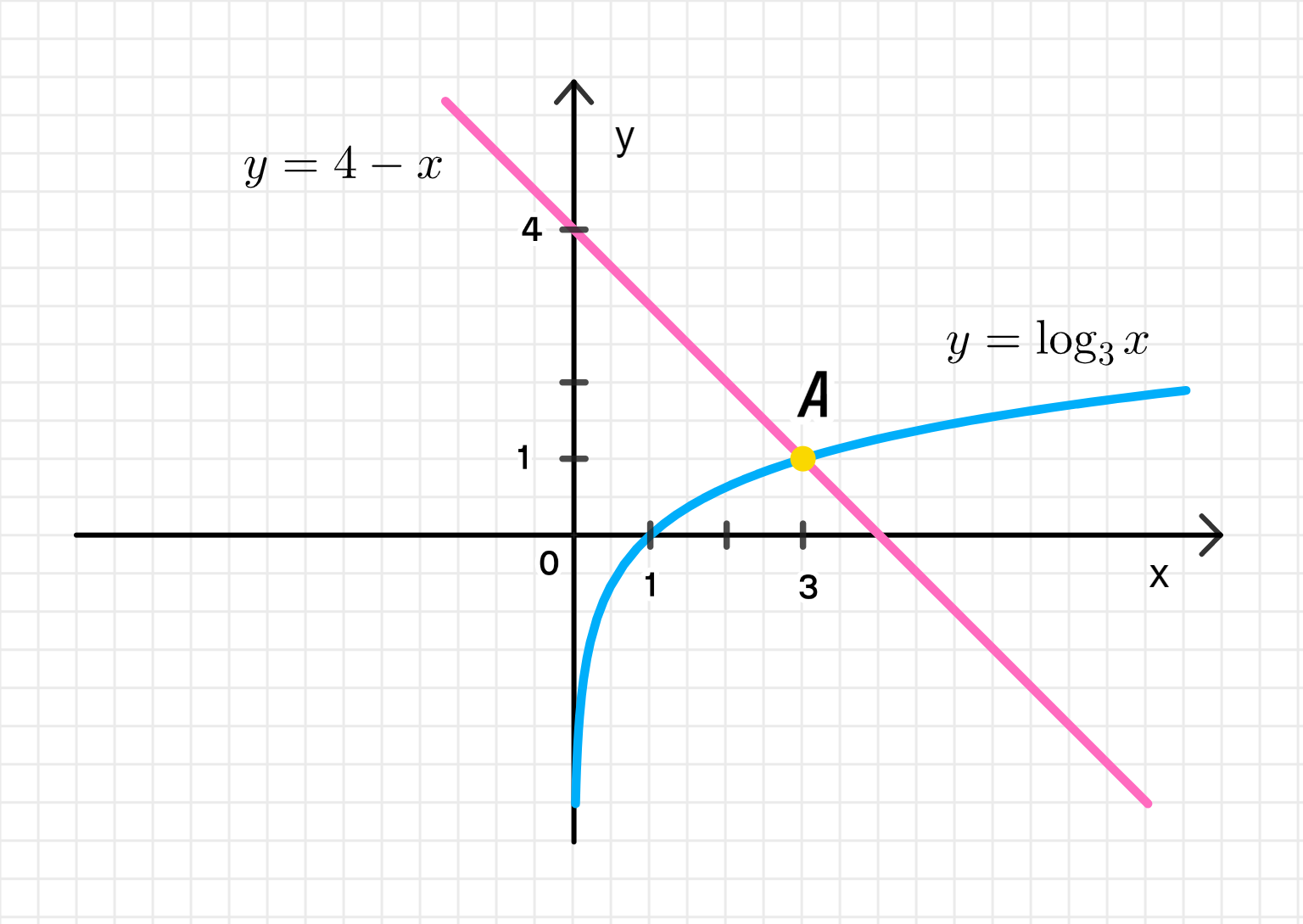
- log3 х = 4 — х;
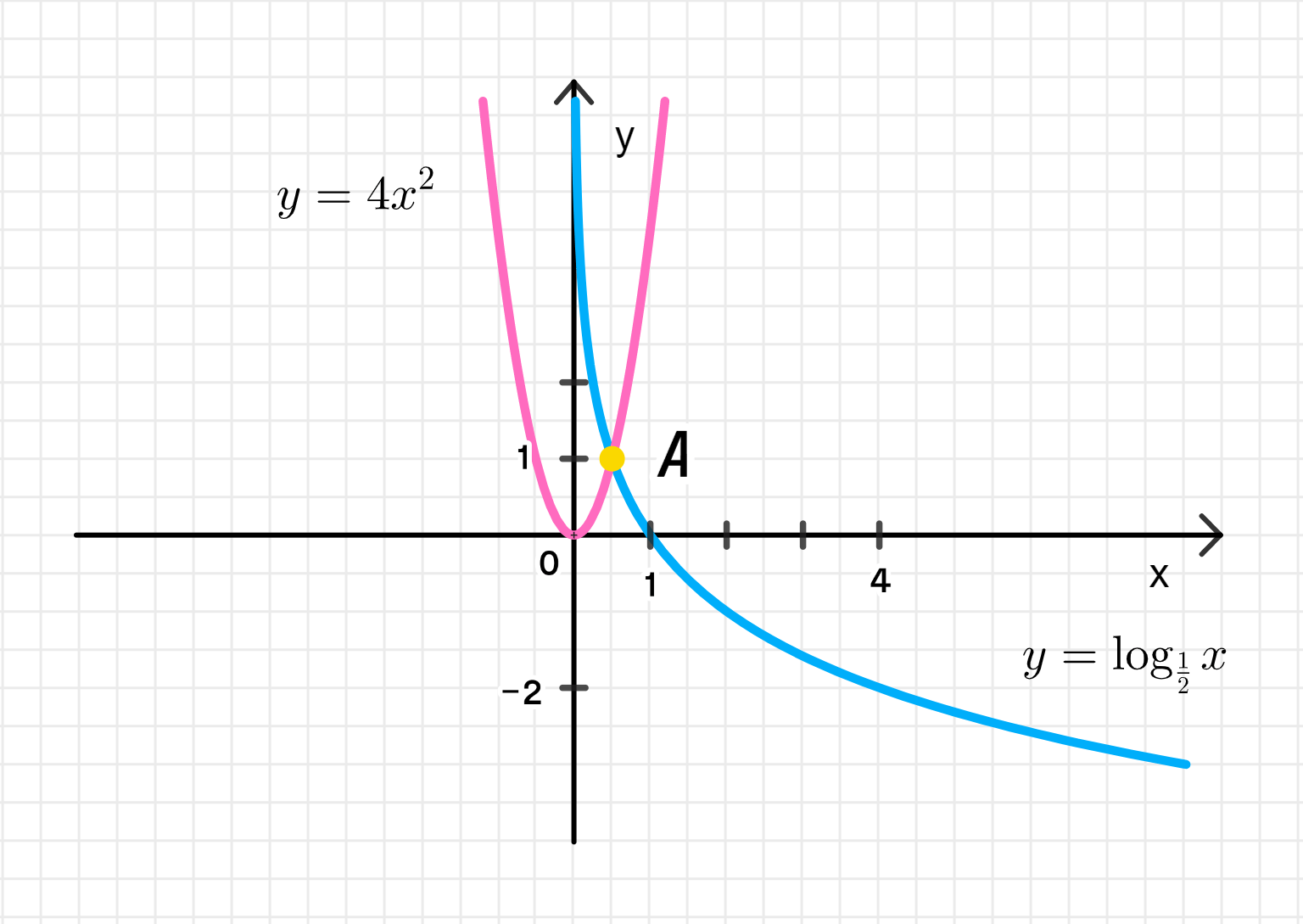
- log1/2(х) = 4х2;
- 2х = log0,5(х);
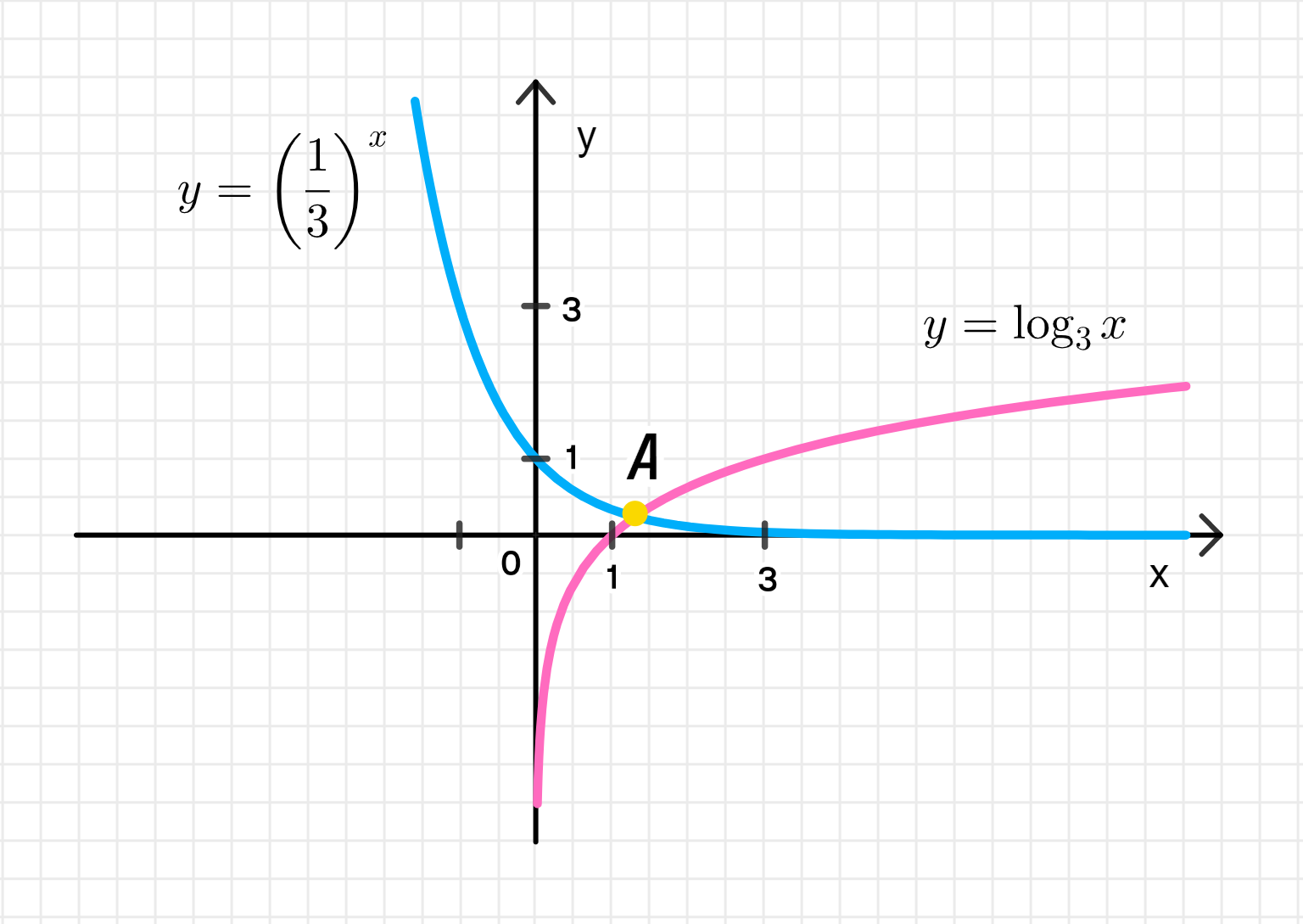
- (1/3)x = log3(х).
1)
Уравнение экспоненты:
Таблица значений:
Уравнение прямой:
Таблица значений:
Графики функций:
Ответ:
2)
Уравнение экспоненты:
Таблица значений:
Уравнение параболы:
Таблица значений:
Графики функций:
Ответ:
3)
Уравнение экспоненты:
Таблица значений:
Уравнение прямой:
Таблица значений:
Графики функций:
Ответ:
4)
Уравнение экспоненты:
Таблица значений:
Уравнение параболы:
Таблица значений:
Графики функций:
Ответ:
5)
Уравнение экспоненты:
Таблица значений:
Уравнение экспоненты:
Таблица значений:
Графики функций:
Ответ:
6)
Уравнение экспоненты:
Таблица значений:
Уравнение экспоненты:
Таблица значений:
Графики функций:
Ответ:
1) Уравнение:
Шаг 1: Проанализируем уравнение
У нас есть два выражения:
- — это экспоненциальная функция с основанием .
- — это линейная функция.
Наша цель — найти значение , при котором эти две функции равны.
Шаг 2: Проверим несколько значений
Для этого мы подставим различные значения в оба выражения и посмотрим, при каком значении они равны.
- Для :
Видим, что и , т.е. — это решение уравнения.
Шаг 3: Ответ
Единственное решение уравнения:
2) Уравнение:
Шаг 1: Проанализируем уравнение
- — это экспоненциальная функция с основанием .
- — это парабола, открывающаяся вниз (так как коэффициент при отрицательный).
Мы ищем значения , при которых эти функции равны.
Шаг 2: Проверим несколько значений
- Для :
Уравнение не выполняется для .
- Для :
Уравнение выполняется для .
- Для :
Уравнение не выполняется для .
- Для :
Уравнение не выполняется для .
- Для :
Уравнение не выполняется для .
Для более точных решений можно использовать численные методы, но на основе этих проверок очевидно, что является одним решением.
Шаг 3: Ответ
Решения:
3) Уравнение:
Шаг 1: Проанализируем уравнение
- — это логарифм с основанием .
- — это линейная функция.
Мы ищем значение , при котором эти функции равны.
Шаг 2: Проверим несколько значений
- Для :
Уравнение не выполняется для .
- Для :
Уравнение выполняется для .
Шаг 3: Ответ
Решение:
4) Уравнение:
Шаг 1: Проанализируем уравнение
- — это логарифм с основанием , который является убывающей функцией.
- — это парабола, открывающаяся вверх.
Мы ищем значение , при котором эти функции равны.
Шаг 2: Проверим несколько значений
- Для :
Уравнение не выполняется для .
- Для :
Уравнение выполняется для .
Шаг 3: Ответ
Решение:
5) Уравнение:
Шаг 1: Проанализируем уравнение
- — это экспоненциальная функция с основанием .
- — это логарифм с основанием , который является убывающей функцией.
Мы ищем значение , при котором эти функции равны.
Шаг 2: Проверим несколько значений
- Для :
Уравнение не выполняется для .
- Для :
Уравнение не выполняется для .
- Для :
Уравнение не выполняется для .
Для более точного нахождения решения можно воспользоваться численным методом, например, методом Ньютона.
Шаг 3: Ответ
При численном решении получаем:
6) Уравнение:
Шаг 1: Проанализируем уравнение
- — это экспоненциальная функция с основанием , которая является убывающей функцией.
- — это логарифм с основанием , который является возрастающей функцией.
Мы ищем значение , при котором эти функции равны.
Шаг 2: Проверим несколько значений
- Для :
Уравнение не выполняется для .
- Для :
Уравнение не выполняется для .
При численном решении получаем:
Шаг 3: Ответ
Решение:


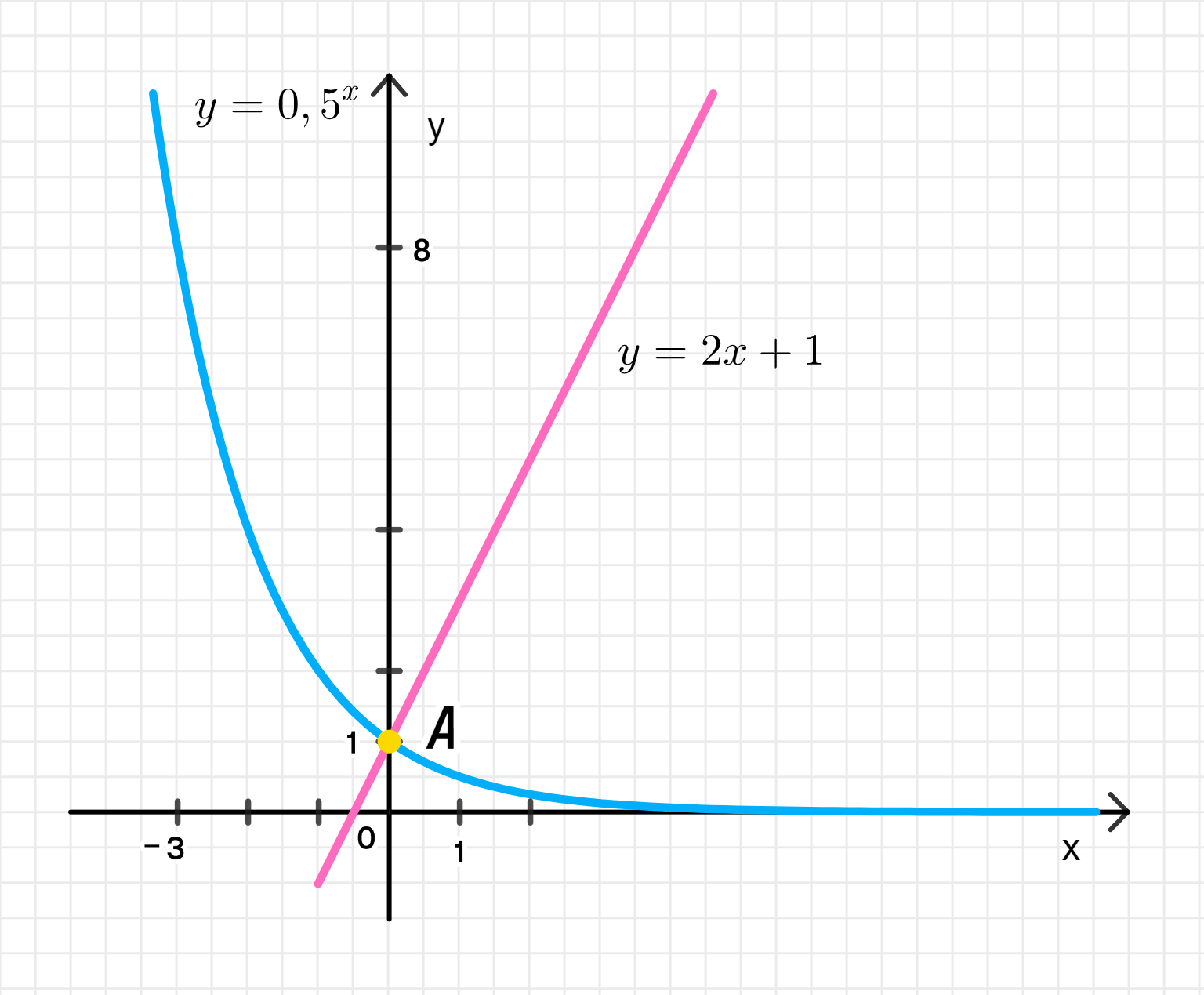
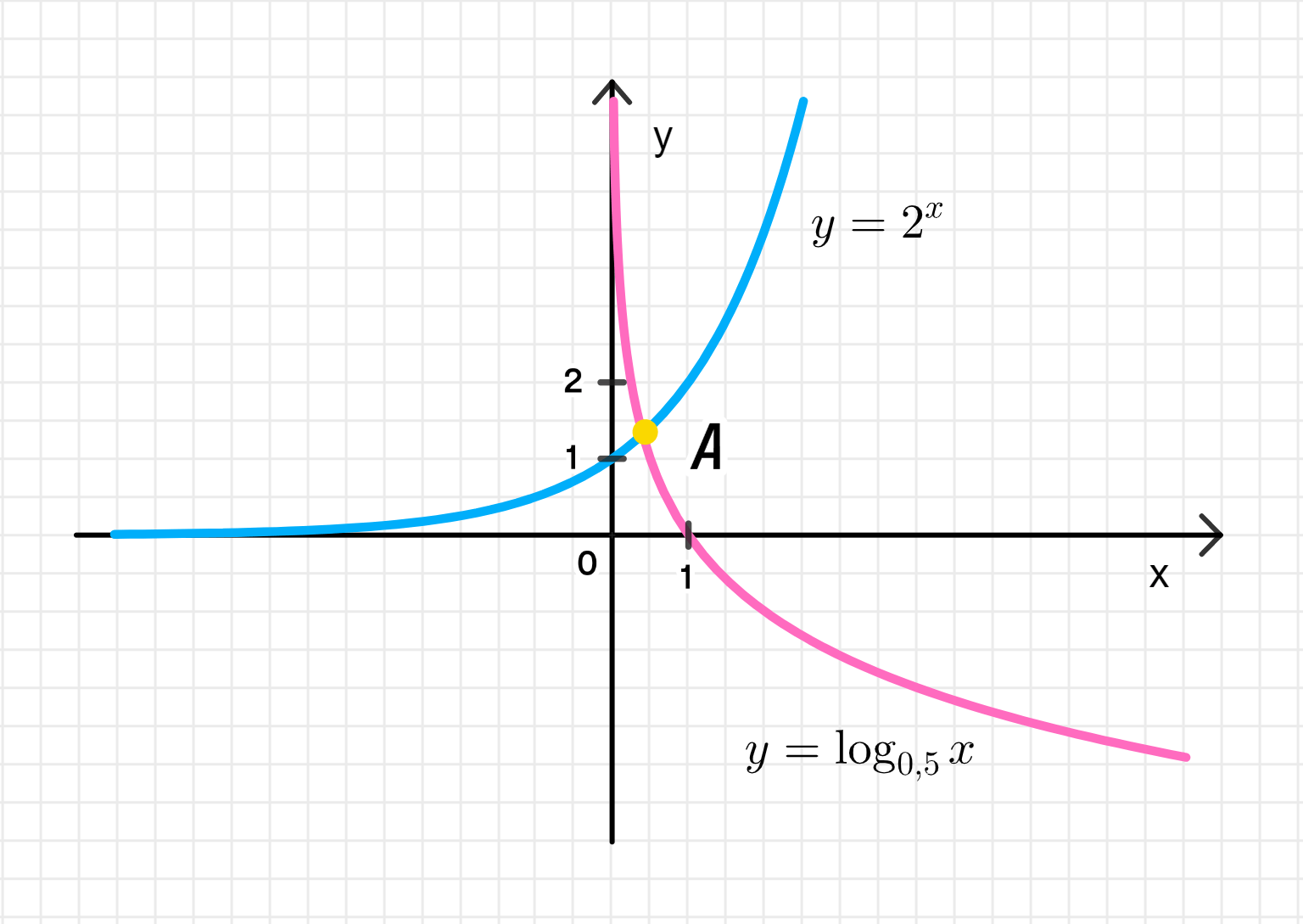

Оставь свой отзыв 💬
Комментариев пока нет, будьте первым!