
Учебник «Алгебра» для 10-11 классов под авторством Алимова – это один из наиболее популярных и широко используемых учебных пособий для старшеклассников. Он заслужил признание как среди учителей, так и среди учеников благодаря своей структурированности, доступности изложения и качественной проработке материала.
ГДЗ по Алгебре 10-11 Класс Номер 134 Алимов — Подробные Ответы
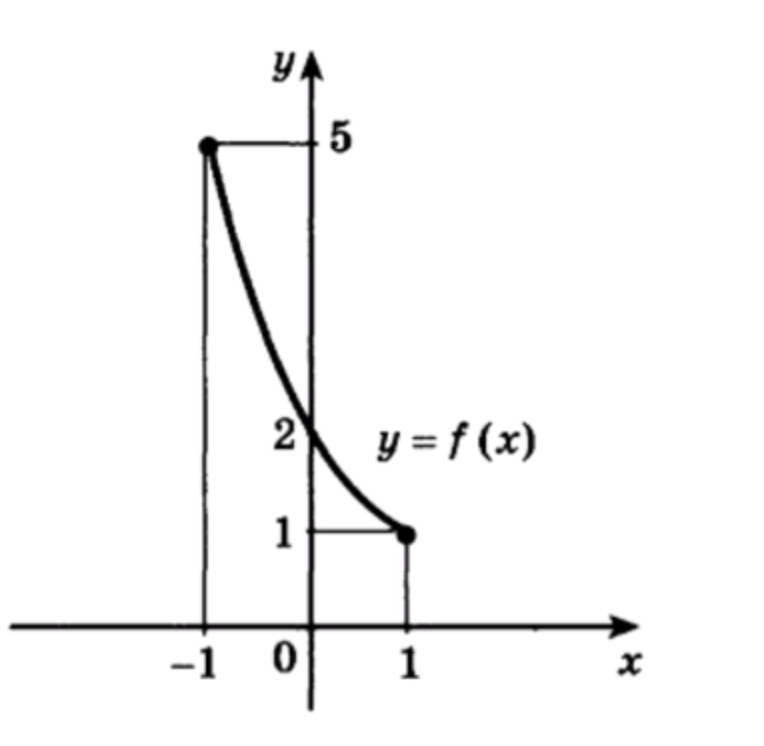
Функция у = f (х) задана графиком (рис. 21). Построить график функции, обратной к данной.
а) Функция задана графиком на рисунке. Построим график функции обратной к данной.
Так как график обратной функции симметричен графику данной функции относительно прямой :
Точка симметричная точке относительно прямой — точка .
Точка симметричная точке относительно прямой — точка .
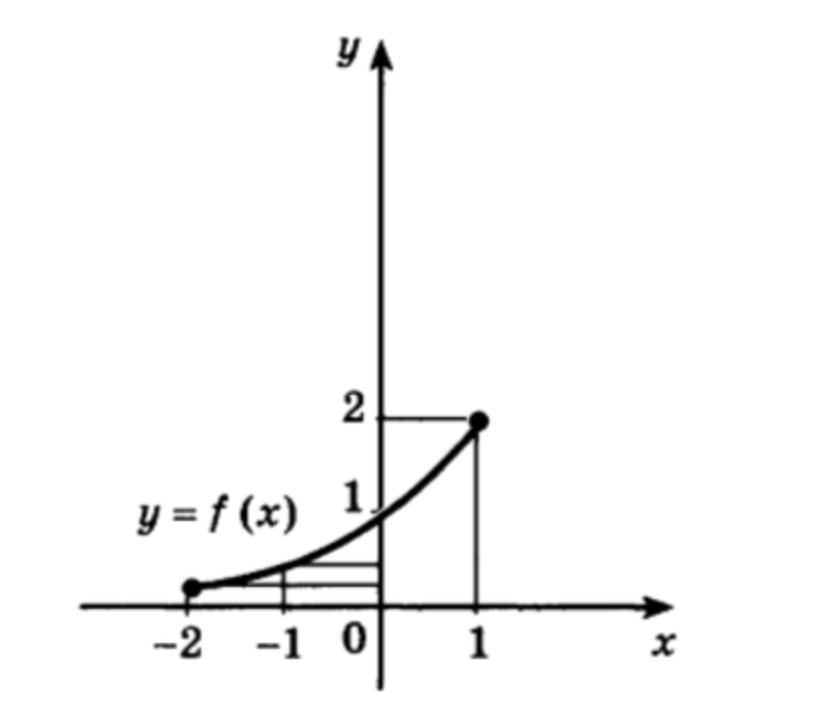
б) Функция задана графиком на рисунке. Построим график функции обратной к данной.
Так как график обратной функции симметричен графику данной функции относительно прямой :
Точка симметричная точке относительно прямой — точка .
Точка симметричная точке относительно прямой — точка .
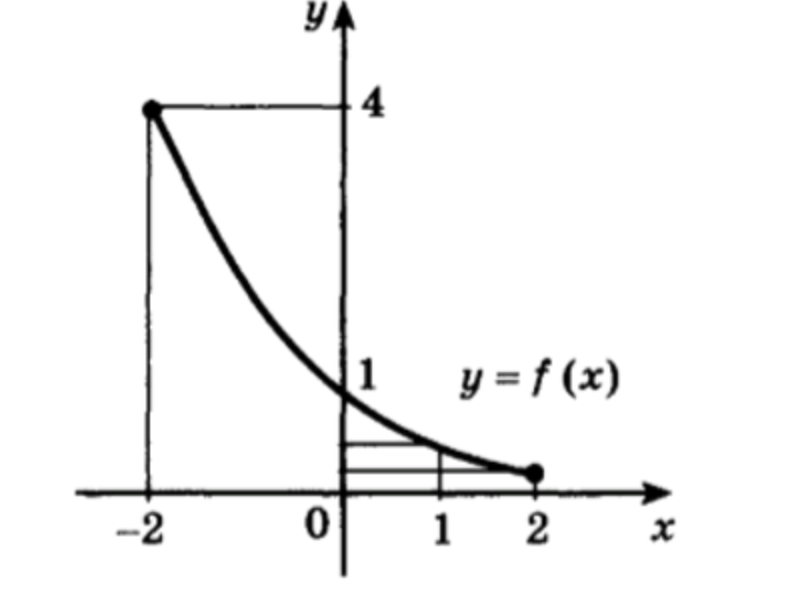
в) Функция задана графиком на рисунке. Построим график функции обратной к данной.
Так как график обратной функции симметричен графику данной функции относительно прямой :
Точка симметричная точке относительно прямой — точка .
Точка симметричная точке относительно прямой — точка .
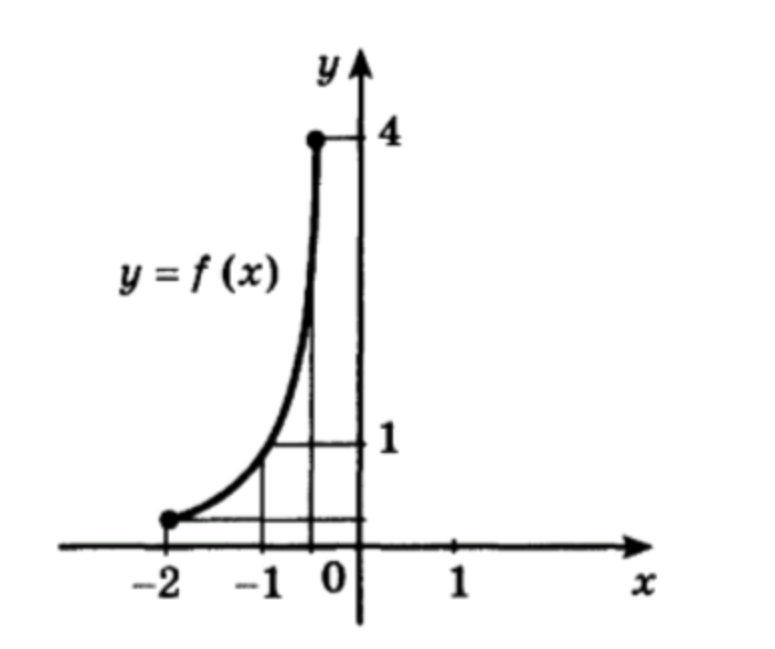
г) Функция задана графиком на рисунке. Построим график функции обратной к данной.
Так как график обратной функции симметричен графику данной функции относительно прямой :
Точка симметричная точке относительно прямой — точка .
Точка симметричная точке относительно прямой — точка .
а) Функция задана графиком на рисунке. Построим график функции обратной к данной.
Симметрия графиков:
График функции обратной симметричен графику исходной функции относительно прямой . Это значит, что для каждой точки на графике исходной функции , точка на графике обратной функции будет .
Работа с точками: Чтобы построить график обратной функции, нужно найти симметричные точки для нескольких известных точек из графика данной функции. Пройдемся по этим точкам:
- Точка (
1 , 1 ) (1, 1) - Точка (
0 , 2 ) (0, 2)
Таким образом, для графика обратной функции можно отметить точки и , которые будут использованы для построения графика.
б) Функция задана графиком на рисунке. Построим график функции обратной к данной.
Симметрия графиков:
Как и в предыдущем случае, график функции обратной симметричен графику исходной функции относительно прямой .
Работа с точками: Для построения графика обратной функции возьмем несколько точек из исходного графика и найдем их симметричные значения относительно прямой .
- Точка (
0 , 1 ) (0, 1) - Точка (
0 , 2 ) (0, 2)
Таким образом, для графика обратной функции отмечаем точки и .
в) Функция задана графиком на рисунке. Построим график функции обратной к данной.
Симметрия графиков:
Как и в предыдущих случаях, график функции обратной симметричен графику исходной функции относительно прямой .
Работа с точками: Для построения графика обратной функции выберем несколько точек из графика исходной функции и найдем их симметричные точки относительно прямой .
- Точка (
− 2 , 4 ) (-2, 4) - Точка (
0 , 1 ) (0, 1)
Таким образом, для графика обратной функции отмечаем точки и .
г) Функция задана графиком на рисунке. Построим график функции обратной к данной.
Симметрия графиков:
График функции обратной симметричен графику исходной функции относительно прямой .
Работа с точками: Для построения графика обратной функции используем несколько точек из исходного графика и находим их симметричные координаты относительно прямой .
- Точка (
− 1 , 1 ) (-1, 1) - Точка : симметричная точка относительно прямой будет , так как координаты меняются местами.
Таким образом, для графика обратной функции отмечаем точки и .
Итог
Для построения графика функции обратной важно понимать, что график симметричен графику исходной функции относительно прямой . Процесс построения сводится к нахождению симметричных точек и их отображению.



Оставь свой отзыв 💬
Комментариев пока нет, будьте первым!