ГДЗ по Алгебре 10-11 Класс Номер 129 Алимов — Подробные Ответы

Построить график функции и указать её область определения, множество значений и промежутки возрастания и убывания; выяснить, является ли функция ограниченной сверху (снизу):

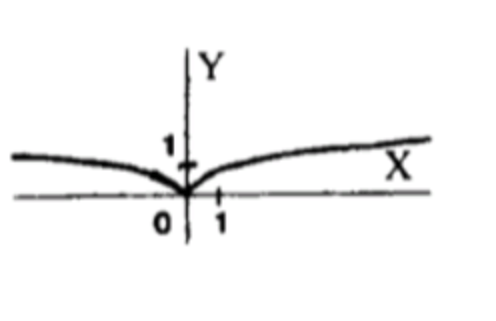
1. у = |x|1/3;
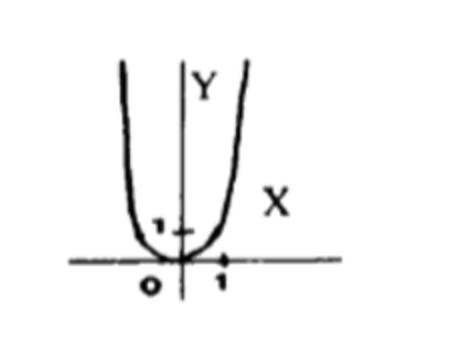
2. y=|x|5;
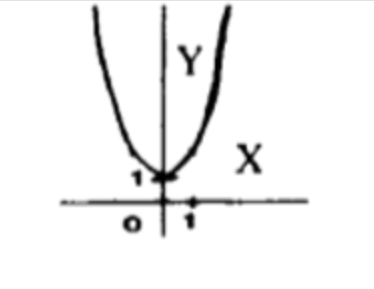
3. y= |x|3+1;
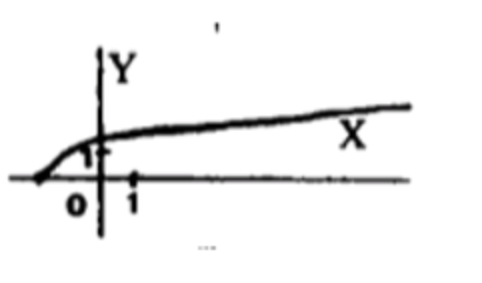
4. у = |x|1/5 — 2;
5. у = |х+5|1/3;
6. у = |2х|^-3.

$y = |x|^{\frac{1}{3}}$;

Функция является чётной:
$y(-x) = |-x|^{\frac{1}{3}} = |x|^{\frac{1}{3}} = y(x);$

Если $x \geq 0$, тогда $y = x^{\frac{1}{3}}$, значит:

• Область определения: $x \in \mathbb{R}$;
• Множество значений: $y \geq 0$;
• Функция убывает на $(-\infty; 0)$ и возрастает на $(0; +\infty)$;
• Функция ограничена снизу;

Координаты некоторых точек:

$y = |x|^5$;

Функция является чётной:
$y(-x) = |-x|^5 = |x|^5 = y(x);$

Если $x \geq 0$, тогда $y = x^5$, значит:

• Область определения: $x \in \mathbb{R}$;
• Множество значений: $y \geq 0$;
• Функция убывает на $(-\infty; 0)$ и возрастает на $(0; +\infty)$;
• Функция ограничена снизу;

Координаты некоторых точек:

$y = |x|^3 + 1$;

Функция является чётной:
$y(-x) = |-x|^3 + 1 = |x|^3 + 1 = y(x);$

Если $x \geq 0$, тогда $y = x^3 + 1$, значит:

• Область определения: $x \in \mathbb{R}$;
• Множество значений: $y \geq 1$;
• Функция убывает на $(-\infty; 0)$ и возрастает на $(0; +\infty)$;
• Функция ограничена снизу;

Координаты некоторых точек:

$y = |x|^{\frac{1}{5}} — 2$;

Функция является чётной:
$y(-x) = |-x|^{\frac{1}{5}} — 2 = |x|^{\frac{1}{5}} — 2 = y(x);$

Если $x \geq 0$, тогда $y = x^{\frac{1}{5}} — 2$, значит:

• Область определения: $x \in \mathbb{R}$;
• Множество значений: $y \geq -2$;
• Функция убывает на $(-\infty; 0)$ и возрастает на $(0; +\infty)$;
• Функция ограничена снизу;

Координаты некоторых точек:

$y = |x + 2|^{\frac{1}{3}}$;

График данной функции является графиком функции $y = |x|^{\frac{1}{3}}$, сдвинутым вдоль оси абсцисс на 2 единицы влево;

Если $x \geq -2$, тогда $y = (x + 2)^{\frac{1}{3}}$, значит:

• Область определения: $x \in \mathbb{R}$;
• Множество значений: $y \geq 0$;
• Функция убывает на $(-\infty; -2)$ и возрастает на $(-2; +\infty)$;
• Функция ограничена снизу;

Координаты некоторых точек:

$y = |2x|^{-3}$;

Функция является чётной:
$y(-x) = |-2x|^{-3} = |2x|^{-3} = y(x);$

Если $x \geq 0$, тогда $y = (2x)^{-3}$, значит:

• Область определения: $x \ne 0$;
• Множество значений: $y > 0$;
• Функция возрастает на $(-\infty; 0)$ и убывает на $(0; +\infty)$;
• Функция ограничена снизу

1) $y = |x|^{\frac{1}{3}}$

Шаг 1. Понимание функции

Запись $|x|^{\frac{1}{3}}$ — это корень третьей степени из модуля x.
Или:

$$y = \left( |x| \right)^{1/3}$$

Шаг 2. Чётность

Проверим:

$$y(-x) = |-x|^{1/3} = |x|^{1/3} = y(x)$$

→ Функция чётная (симметрична относительно оси OY).

Шаг 3. Область определения

Модуль и корень третьей степени определены при всех x:
→ Область определения: $D(y) = \mathbb{R}$

Шаг 4. Множество значений

Модуль всегда неотрицателен, а $\sqrt[3]{x}$ определён при любом x ≥ 0:

$$|x| \geq 0 \Rightarrow |x|^{1/3} \geq 0$$

→ Множество значений: $E(y) = [0, +\infty)$

Шаг 5. Поведение

• При $x > 0$: $y = x^{1/3}$ — функция возрастает
• При $x < 0$: $y = (-x)^{1/3} = |x|^{1/3}$ — та же функция
  → Функция убывает на $(-\infty, 0)$ и возрастает на $(0, +\infty)$

Шаг 6. Ограниченность

Наименьшее значение достигается при $x = 0$: $y = 0$
→ Ограничена снизу нулём

Шаг 7. Некоторые точки

$$\begin{array}{|c|c|c|c|} \hline x & 0 & 1 & 8 \\ \hline y & 0 & 1 & 2 \\ \hline \end{array}$$

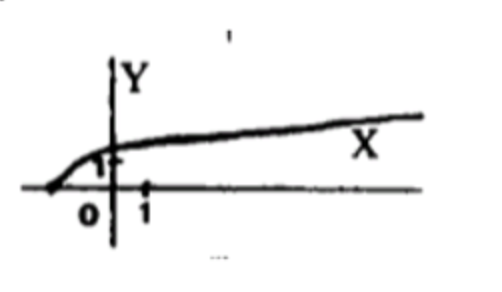
Шаг 8. График

График симметричен относительно оси OY, плавно изгибается вверх, проходит через точку (0,0), форма — «мягкий угол».

2) $y = |x|^5$

Шаг 1. Распознавание

Степенная функция с нечётной натуральной степенью и модулем:

$$y = (|x|)^5$$

Шаг 2. Чётность

$$y(-x) = |-x|^5 = |x|^5 = y(x) \Rightarrow \text{чётная}$$

Шаг 3. Область определения

Любое вещественное x можно возвести в степень:
→ $D(y) = \mathbb{R}$

Шаг 4. Множество значений

$$|x| \geq 0 \Rightarrow |x|^5 \geq 0 \Rightarrow y \geq 0$$

→ $E(y) = [0, +\infty)$

Шаг 5. Поведение

• Убывает на $(-\infty, 0)$
• Возрастает на $(0, +\infty)$

Шаг 6. Ограниченность

Минимум при $x = 0$: $y = 0$

Шаг 7. Точки

$$\begin{array}{|c|c|c|c|} \hline x & 0 & 1 & 2 \\ \hline y & 0 & 1 & 32 \\ \hline \end{array}$$

Шаг 8. График

Симметричен, круто возрастает при больших |x|. Похож на параболу, но острее.

3) $y = |x|^3 + 1$

Шаг 1. Распознавание

Комбинация степенной и линейной функции:

$$y = (|x|)^3 + 1$$

Шаг 2. Чётность

$$y(-x) = |-x|^3 + 1 = |x|^3 + 1 = y(x) \Rightarrow \text{чётная}$$

Шаг 3. Область определения

→ $D(y) = \mathbb{R}$

Шаг 4. Множество значений

$$|x|^3 \geq 0 \Rightarrow |x|^3 + 1 \geq 1$$

→ $E(y) = [1, +\infty)$

Шаг 5. Поведение

• Убывает на $(-\infty, 0)$
• Возрастает на $(0, +\infty)$

Шаг 6. Ограниченность

Минимум при $x = 0$: $y = 1$

Шаг 7. Точки

$$\begin{array}{|c|c|c|c|} \hline x & 0 & 1 & 2 \\ \hline y & 1 & 2 & 9 \\ \hline \end{array}$$

Шаг 8. График

Как график $|x|^3$, но смещён вверх на 1.

4) $y = |x|^{\frac{1}{5}} — 2$

Шаг 1. Распознавание

Корень пятой степени + вертикальный сдвиг:

$$y = \left( |x| \right)^{1/5} — 2$$

Шаг 2. Чётность

$$y(-x) = |x|^{1/5} — 2 = y(x)$$

Шаг 3. Область определения

→ $D(y) = \mathbb{R}$

Шаг 4. Множество значений

$$|x|^{1/5} \geq 0 \Rightarrow y \geq -2$$

Шаг 5. Поведение

• Убывает на $(-\infty, 0)$
• Возрастает на $(0, +\infty)$

Шаг 6. Ограниченность

Минимум при $x = 0$: $y = -2$

Шаг 7. Точки

$$\begin{array}{|c|c|c|c|} \hline x & 0 & 1 & 32 \\ \hline y & -2 & -1 & 0 \\ \hline \end{array}$$

Шаг 8. График

График похож на $|x|^{1/5}$, но сдвинут вниз на 2.

5) $y = |x + 2|^{\frac{1}{3}}$

Шаг 1. Распознавание

Сдвиг функции $y = |x|^{1/3}$ на 2 влево.

Шаг 2. Чётность

Не совсем обычная чётность, но по модулю остаётся симметричной вокруг x = -2.

Шаг 3. Область определения

→ $D(y) = \mathbb{R}$

Шаг 4. Значения

$$y \geq 0$$

Шаг 5. Поведение

• Убывает на $(-\infty; -2)$
• Возрастает на $(-2; +\infty)$

Шаг 6. Ограничена снизу

→ Минимум $y = 0$ при $x = -2$

Шаг 7. Точки

$$\overline{)\begin{array}{cccc}x& -2& -1& 6\\ y& 0& 1& 2\end{array}}$$

Шаг 8. График

6) $y = |2x|^{-3}$

Шаг 1. Распознавание

Функция убывающей степени отрицательного порядка.

Шаг 2. Чётность

$$y(-x) = |-2x|^{-3} = |2x|^{-3} = y(x)$$

Шаг 3. Область определения

$$|2x| \ne 0 \Rightarrow x \ne 0$$

Шаг 4. Значения

$$|2x|^{-3} > 0 \Rightarrow y > 0$$

Шаг 5. Поведение

• Возрастает на $(-\infty, 0)$
• Убывает на $(0, +\infty)$

Шаг 6. Ограниченность

→ Снизу ограничена (но стремится к ∞ при x → 0)

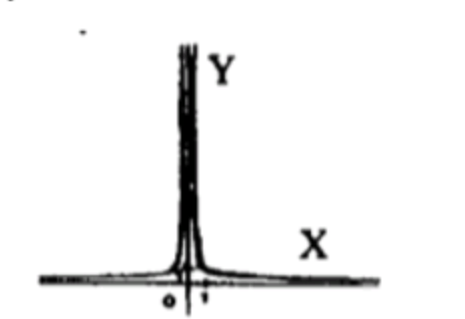
Шаг 7. График

Похожа на гиперболу, вертикальная асимптота при $x=0$

$$x = 0