
Учебник «Алгебра» для 10-11 классов под авторством Алимова – это один из наиболее популярных и широко используемых учебных пособий для старшеклассников. Он заслужил признание как среди учителей, так и среди учеников благодаря своей структурированности, доступности изложения и качественной проработке материала.
ГДЗ по Алгебре 10-11 Класс Номер 127 Алимов — Подробные Ответы
Изобразить схематически график функции и найти её область определения и множество значений; выяснить, является ли функция возрастающей (убывающей), ограниченной сверху (снизу):
- у = (х — 2)7;
- у = (х + 1 )6;
- у = (х + 2)^-2;
- у = (х-1)^-3.
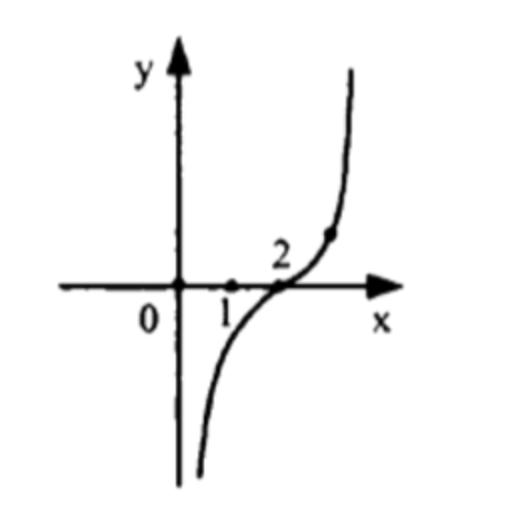
1)
График данной функции является графиком функции , сдвинутым вдоль оси абсцисс на 2 единицы вправо, значит:
- Область определения:
- Множество значений:
- Функция является возрастающей;
- Функция не является ограниченной;
Схематический график функции:
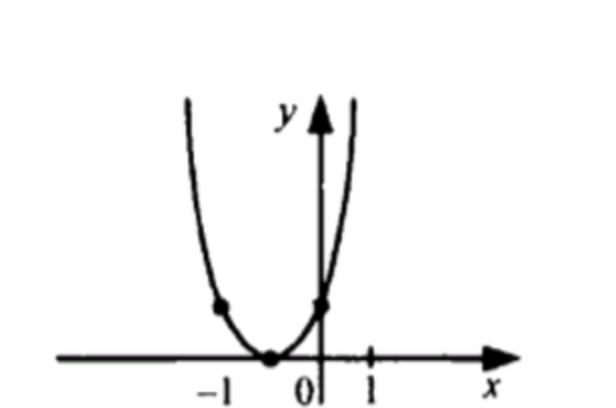
2)
График данной функции является графиком функции , сдвинутым вдоль оси абсцисс на 1 единицу влево, значит:
- Область определения:
- Множество значений:
- Функция является возрастающей;
- Функция не является ограниченной;
Схематический график функции:
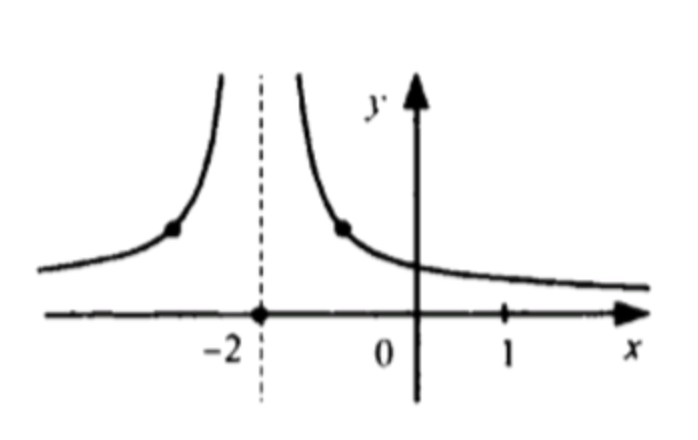
3)
График данной функции является графиком функции , сдвинутым вдоль оси абсцисс на 2 единицы влево, значит:
- Область определения:
- Множество значений:
- Функция возрастает на и убывает на
- Функция ограничена снизу;
Схематический график функции:
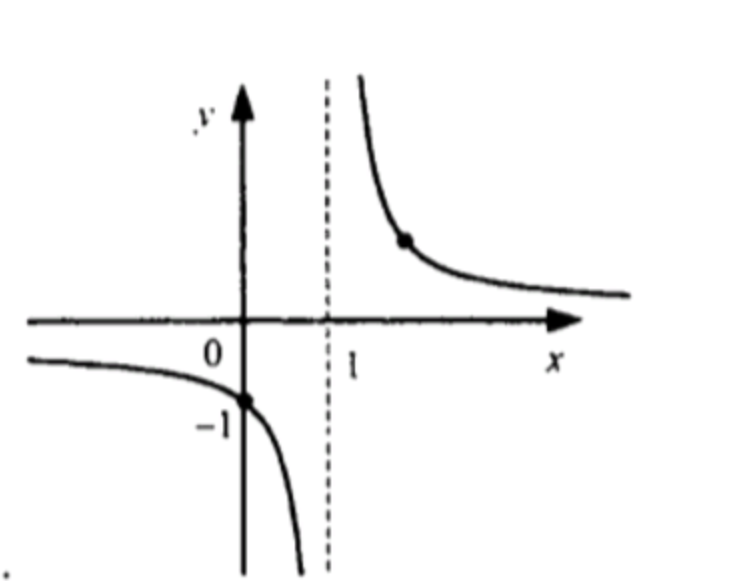
4)
График данной функции является графиком функции , сдвинутым вдоль оси абсцисс на 1 единицу вправо, значит:
- Область определения:
- Множество значений:
- Функция убывает на всей области определения;
- Функция не является ограниченной;
Схематический график функции:
Ответ:
1) Функция
Анализ функции
Данная функция представляет собой степенную функцию вида , но сдвинутую вдоль оси X на 2 единицы вправо.
Число 7 – нечетное, значит, функция сохраняет свойство исходной степени:
- Определена на всей числовой прямой
- Значения могут принимать любые числа:
- Функция является возрастающей на всей области определения.
- Не является ограниченной, поскольку при и при .
Исследование поведения функции
При :
Точка – корень функции.
При больших значениях :
- Если , то выражение положительно, а его седьмая степень тоже положительна.
- Если , то .
При малых значениях :
- Если , то выражение отрицательно, а его седьмая степень тоже отрицательна.
- Если , то .
Вывод
- График пересекает ось X в точке (
2 , 0 ) (2, 0) - Функция возрастает на всей области определения.
- Ограничений по значениям нет.
2) Функция
Анализ функции
Данная функция представляет собой степенную функцию , но сдвинутую на 1 единицу влево.
Число 5 – нечетное, значит:
- Функция определена на всей числовой прямой
- Функция принимает любые значения:
- Является возрастающей.
- Неограниченна, поскольку при и при .
Исследование поведения функции
При :
Точка – корень функции.
При больших :
- Если , то положительно, значит, его пятая степень тоже положительна.
- Если , то .
При малых :
- Если , то отрицательно, а его пятая степень тоже отрицательна.
- Если , то .
Вывод
- График проходит через точку (
− 1 , 0 ) (-1, 0) - Функция возрастает на всей числовой прямой.
- Значения неограниченны.
3) Функция
Анализ функции
Эта функция является вариантом степенной функции , но сдвинутой на 2 единицы влево.
Степень -2 – четная и отрицательная, значит:
- Функция определена всюду, кроме точки
- Значения всегда положительны:
- Функция убывает на и возрастает на
- Ограничена снизу:
Исследование поведения функции
При :
- Выражение не определено.
- На графике разрыв в точке .
При :
- При возведении в степень -2 значение стремится к 0.
При :
- При возведении в степень -2 значение также стремится к 0.
При слева и справа:
Значение стремится к +∞.
Вывод
- Функция разрывна в точке
- Возрастает на и убывает на
- Ограничена снизу:
4) Функция
Анализ функции
Эта функция является вариантом , но сдвинутой на 1 вправо.
Степень -3 – нечетная, значит:
- Функция определена всюду, кроме точки x
- Значения могут быть положительными и отрицательными: .
- Функция убывает на всей области определения.
- Не является ограниченной.
Исследование поведения функции
При :
- Выражение не определено.
- График имеет разрыв в этой точке.
При :
- сильно отрицательно.
- Возведение в степень -3 дает значения, стремящиеся к 0.
При :
- становится большим.
- Значение стремится к 0.
При и :
Значение резко уходит в +∞ или -∞.
Вывод
- Функция убывает на всей области определения.
- Разрыв в точке
- Значения могут быть как положительными, так и отрицательными.
Ответ



Оставь свой отзыв 💬
Комментариев пока нет, будьте первым!